Mottatte ligningssystemer bred applikasjon i den økonomiske sektoren matematisk modellering ulike prosesser. For eksempel, når du løser problemer med ledelse og produksjonsplanlegging, logistikkruter ( transportoppgave) eller utstyrsplassering.

Ligningssystemer brukes ikke bare innen matematikk, men også innen fysikk, kjemi og biologi, når man løser problemer med å finne populasjonsstørrelsen.

system lineære ligninger Nevn to eller flere ligninger med flere variabler som det er nødvendig å finne en felles løsning for. En slik tallrekke der alle likninger blir sanne likheter eller beviser at sekvensen ikke eksisterer.

Lineær ligning

Ligninger på formen ax+by=c kalles lineære. Betegnelsene x, y er de ukjente, hvis verdi må finnes, b, a er koeffisientene til variablene, c er ligningens friledd.
Å løse ligningen ved å plotte grafen vil se ut som en rett linje, der alle punktene er løsningen av polynomet.

Typer av systemer av lineære ligninger

De enkleste er eksempler på systemer med lineære ligninger med to variabler X og Y.

F1(x, y) = 0 og F2(x, y) = 0, hvor F1,2 er funksjoner og (x, y) er funksjonsvariabler.

Løs et ligningssystem - det betyr å finne slike verdier (x, y) som systemet blir en ekte likhet for, eller å fastslå at det ikke finnes passende verdier for x og y.

Et verdipar (x, y), skrevet som punktkoordinater, kalles en løsning på et system med lineære ligninger.

Hvis systemene har én felles løsning eller det ikke finnes noen løsning, kalles de likeverdige.

Homogene systemer med lineære ligninger er systemer hvis høyre side er lik null. Hvis den høyre delen etter "lik"-tegnet har en verdi eller er uttrykt av en funksjon, er ikke et slikt system homogent.

Antall variabler kan være mye mer enn to, da bør vi snakke om et eksempel på et system av lineære ligninger med tre variabler eller flere.

Overfor systemer antar skolebarn at antall ligninger nødvendigvis må falle sammen med antall ukjente, men dette er ikke tilfelle. Antall ligninger i systemet er ikke avhengig av variablene, det kan være et vilkårlig stort antall av dem.

Enkle og komplekse metoder for å løse ligningssystemer

Det finnes ingen generell analytisk måte å løse slike systemer på, alle metoder er basert på numeriske løsninger. Skolekurset i matematikk beskriver i detalj metoder som permutasjon, algebraisk addisjon, substitusjon, samt den grafiske og matrisemetoden, løsningen etter Gauss-metoden.

Hovedoppgaven i undervisningsmetoder for løsning er å lære hvordan man korrekt analyserer systemet og finner den optimale løsningsalgoritmen for hvert eksempel. Det viktigste er ikke å huske et system med regler og handlinger for hver metode, men å forstå prinsippene for å bruke en bestemt metode.

Løsningen av eksempler på systemer med lineære ligninger i 7. klasse på det generelle skoleprogrammet er ganske enkel og er forklart i detalj. I enhver lærebok om matematikk er denne delen viet nok oppmerksomhet. Løsningen av eksempler på systemer med lineære ligninger ved metoden til Gauss og Cramer studeres mer detaljert i de første kursene til høyere utdanningsinstitusjoner.

Løsning av systemer ved substitusjonsmetoden

Handlingene til substitusjonsmetoden er rettet mot å uttrykke verdien av en variabel gjennom den andre. Uttrykket settes inn i den gjenværende ligningen, deretter reduseres det til en enkelt variabelform. Handlingen gjentas avhengig av antall ukjente i systemet

La oss gi et eksempel på et system med lineære ligninger av 7. klasse ved substitusjonsmetoden:

Som man kan se fra eksemplet, ble variabelen x uttrykt gjennom F(X) = 7 + Y. Det resulterende uttrykket, substituert inn i den andre ligningen av systemet i stedet for X, bidro til å oppnå én variabel Y i den andre ligningen . Løsningen i dette eksemplet forårsaker ikke vanskeligheter og lar deg få Y-verdien. Siste steg dette er en test av de mottatte verdiene.

Det er ikke alltid mulig å løse et eksempel på et system med lineære ligninger ved substitusjon. Ligningene kan være komplekse og uttrykket av variabelen i form av den andre ukjente vil være for tungvint for videre beregninger. Når det er mer enn 3 ukjente i systemet, er også substitusjonsløsningen upraktisk.

Løsning av et eksempel på et system med lineære inhomogene ligninger:

Løsning med algebraisk addisjon

Når man søker etter en løsning på systemer ved addisjonsmetoden, utføres ledd-for-ledd addisjon og multiplikasjon av ligninger med forskjellige tall. Det endelige målet for matematiske operasjoner er en ligning med én variabel.

For applikasjoner denne metoden det krever øvelse og observasjon. Det er ikke lett å løse et system av lineære ligninger ved hjelp av addisjonsmetoden med antall variabler 3 eller flere. Algebraisk addisjon er nyttig når ligningene inneholder brøker og desimaltall.

Løsningshandlingsalgoritme:

1. Multipliser begge sider av ligningen med et tall. Som et resultat av den aritmetiske operasjonen må en av koeffisientene til variabelen bli lik 1.
2. Legg til det resulterende uttrykket term for term og finn en av de ukjente.
3. Bytt inn den resulterende verdien i den andre ligningen i systemet for å finne den gjenværende variabelen.

Løsningsmetode ved å introdusere en ny variabel

En ny variabel kan introduseres hvis systemet trenger å finne en løsning for ikke mer enn to ligninger, antall ukjente bør heller ikke være mer enn to.

Metoden brukes til å forenkle en av ligningene ved å introdusere en ny variabel. Den nye ligningen løses med hensyn til den angitte ukjente, og den resulterende verdien brukes til å bestemme den opprinnelige variabelen.

Det kan ses av eksemplet at ved å introdusere en ny variabel t, var det mulig å redusere systemets 1. ligning til et standard kvadrattrinomial. Du kan løse et polynom ved å finne diskriminanten.

Det er nødvendig å finne verdien av diskriminanten ved å bruke den velkjente formelen: D = b2 - 4*a*c, hvor D er den ønskede diskriminanten, b, a, c er multiplikatorene til polynomet. I det gitte eksemplet er a=1, b=16, c=39, derav D=100. Hvis diskriminanten er større enn null, er det to løsninger: t = -b±√D / 2*a, hvis diskriminanten er mindre enn null, er det bare én løsning: x= -b / 2*a.

Løsningen for de resulterende systemene er funnet ved addisjonsmetoden.

En visuell metode for å løse systemer

Egnet for systemer med 3 ligninger. Metoden består i å plotte grafer for hver ligning som inngår i systemet på koordinataksen. Koordinatene til skjæringspunktene til kurvene og vil være felles løsning systemer.

Den grafiske metoden har en rekke nyanser. Tenk på flere eksempler på å løse systemer av lineære ligninger på en visuell måte.

Som det fremgår av eksemplet, ble to punkter konstruert for hver linje, verdiene til variabelen x ble valgt vilkårlig: 0 og 3. Basert på verdiene til x ble verdiene for y funnet: 3 og 0. Punkter med koordinater (0, 3) og (3, 0) ble markert på grafen og forbundet med en linje.

Trinnene må gjentas for den andre ligningen. Skjæringspunktet mellom linjene er løsningen til systemet.

I følgende eksempel er det nødvendig å finne en grafisk løsning på systemet med lineære ligninger: 0,5x-y+2=0 og 0,5x-y-1=0.

Som det fremgår av eksempelet, har systemet ingen løsning, fordi grafene er parallelle og ikke krysser i hele lengden.

Systemene fra eksempel 2 og 3 er like, men når de er konstruert, blir det åpenbart at løsningene deres er forskjellige. Det skal huskes at det ikke alltid er mulig å si om systemet har en løsning eller ikke, det er alltid nødvendig å bygge en graf.

Matrix og dens varianter

Matriser brukes til å kort skrive ned et system med lineære ligninger. En matrise er en spesiell type tabell fylt med tall. n*m har n - rader og m - kolonner.

En matrise er kvadratisk når antall kolonner og rader er likt. En matrise-vektor er en enkelt-kolonne matrise med et uendelig mulig antall rader. En matrise med enheter langs en av diagonalene og andre nullelementer kalles identitet.

En invers matrise er en slik matrise, når multiplisert med hvilken den opprinnelige blir til en enhet én, eksisterer en slik matrise bare for den opprinnelige kvadratiske.

Regler for å transformere et ligningssystem til en matrise

Når det gjelder ligningssystemer, er koeffisientene og frie medlemmer av ligningene skrevet som tall på matrisen, én ligning er én rad i matrisen.

En matriserad kalles ikke-null hvis minst ett element i raden ikke er lik null. Derfor, hvis antallet variabler er forskjellig i noen av ligningene, er det nødvendig å angi null i stedet for den manglende ukjente.

Kolonnene i matrisen må strengt tatt samsvare med variablene. Dette betyr at koeffisientene til variabelen x bare kan skrives i én kolonne, for eksempel den første, koeffisienten til den ukjente y - bare i den andre.

Når du multipliserer en matrise, multipliseres alle matriseelementer suksessivt med et tall.

Alternativer for å finne den inverse matrisen

Formelen for å finne den inverse matrisen er ganske enkel: K -1 = 1 / |K|, der K -1 er den inverse matrisen og |K| - matrisedeterminant. |K| må ikke være lik null, da har systemet en løsning.

Determinanten beregnes enkelt for en to-og-to-matrise, det er bare nødvendig å multiplisere elementene diagonalt med hverandre. For alternativet "tre av tre" er det en formel |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + a 3 b 2 c 1 . Du kan bruke formelen, eller du kan huske at du må ta ett element fra hver rad og hver kolonne slik at kolonne- og radnummerene til elementene ikke gjentar seg i produktet.

Løsning av eksempler på systemer av lineære ligninger ved matrisemetoden

Matrisemetoden for å finne en løsning gjør det mulig å redusere tungvinte oppføringer ved løsning av systemer med et stort antall variabler og ligninger.

I eksemplet er a nm koeffisientene til ligningene, matrisen er en vektor x n er variablene, og b n er de frie leddene.

Løsning av systemer etter Gauss-metoden

I høyere matematikk studeres Gauss-metoden sammen med Cramer-metoden, og prosessen med å finne en løsning på systemer kalles Gauss-Cramer-metoden for løsning. Disse metodene brukes til å finne variablene til systemer med et stort antall lineære ligninger.

Gaussmetoden ligner veldig på substitusjons- og algebraiske addisjonsløsninger, men er mer systematisk. I skolekurset brukes Gauss-løsningen for systemer med 3 og 4 likninger. Hensikten med metoden er å bringe systemet til form av en omvendt trapes. Ved algebraiske transformasjoner og substitusjoner finnes verdien av én variabel i en av systemets ligninger. Den andre ligningen er et uttrykk med 2 ukjente, og 3 og 4 - med henholdsvis 3 og 4 variabler.

Etter å ha brakt systemet til den beskrevne formen, reduseres den videre løsningen til sekvensiell substitusjon av kjente variabler i systemets ligninger.

PÅ skole lærebøker for klasse 7 er et eksempel på en løsning med Gauss-metoden beskrevet som følger:

Som man kan se fra eksemplet, ble det ved trinn (3) oppnådd to ligninger 3x 3 -2x 4 =11 og 3x 3 +2x 4 =7. Løsningen av en av ligningene vil tillate deg å finne ut en av variablene x n.

Teorem 5, som er nevnt i teksten, sier at hvis en av systemets likninger erstattes med en ekvivalent, så vil det resulterende systemet også være ekvivalent med det opprinnelige.

Gauss-metoden er vanskelig for elevene å forstå videregående skole, men er en av de mest interessante måtene å utvikle oppfinnsomheten til barn som er påmeldt programmet fordypning i matte- og fysikktimene.

For å gjøre det enklere å registrere beregninger, er det vanlig å gjøre følgende:

Ligningskoeffisienter og friledd skrives i form av en matrise, der hver rad i matrisen tilsvarer en av systemets ligninger. skiller venstre side av ligningen fra høyre side. Romertall angir antall ligninger i systemet.

Først skriver de ned matrisen som de skal jobbe med, deretter alle handlingene som utføres med en av radene. Den resulterende matrisen skrives etter "pil"-tegnet og fortsett å utføre de nødvendige algebraiske operasjonene til resultatet er oppnådd.

Som et resultat bør en matrise oppnås der en av diagonalene er 1, og alle andre koeffisienter er lik null, det vil si at matrisen er redusert til en enkelt form. Vi må ikke glemme å gjøre beregninger med tallene på begge sider av ligningen.

Denne notasjonen er mindre tungvint og lar deg ikke bli distrahert av å liste opp mange ukjente.

Den gratis bruken av enhver løsningsmetode vil kreve omsorg og en viss mengde erfaring. Ikke alle metoder brukes. Noen måter å finne løsninger på er mer å foretrekke i et bestemt område av menneskelig aktivitet, mens andre eksisterer for læringsformål.

Systemer av lineære ligninger. Forelesning 6

Systemer av lineære ligninger.

Enkle konsepter.

visningssystem

kalt system - lineære ligninger med ukjente.

Tall , , kalles systemkoeffisienter.

Tall kalles gratis medlemmer av systemet, – systemvariabler. Matrise

kalt hovedmatrisen til systemet, og matrisen

– utvidet matrisesystem. Matriser - kolonner

Og tilsvarende matriser av gratis medlemmer og ukjente av systemet. Deretter, i matriseform, kan ligningssystemet skrives som . Systemløsning kalles verdiene til variablene, når de erstatter dem, blir alle likningene i systemet til sanne numeriske likheter. Enhver løsning av systemet kan representeres som en matrise-kolonne. Da er matriselikheten sann.

Ligningssystemet kalles ledd hvis den har minst én løsning og uforenlig hvis det ikke har noen løsning.

Å løse et system med lineære ligninger betyr å finne ut om det er kompatibelt og, hvis det er kompatibelt, å finne den generelle løsningen.

Systemet kalles homogen hvis alle dens frie termer er lik null. Et homogent system er alltid kompatibelt fordi det har en løsning

Kronecker-Kopelli-teoremet.

Svaret på spørsmålet om eksistensen av løsninger av lineære systemer og deres unikhet lar oss oppnå følgende resultat, som kan formuleres som følgende utsagn om et system av lineære ligninger med ukjente

(1)

Teorem 2. Systemet med lineære ligninger (1) er konsistent hvis og bare hvis rangeringen til hovedmatrisen er lik rangeringen til den utvidede (.

Teorem 3. Hvis rangeringen av hovedmatrisen til et felles system av lineære ligninger er lik antall ukjente, så har systemet en unik løsning.

Teorem 4. Hvis rangeringen av hovedmatrisen til et felles system er mindre enn antall ukjente, så har systemet et uendelig antall løsninger.

Regler for løsning av systemer.

3. Finn uttrykket til hovedvariablene i form av de frie og få den generelle løsningen til systemet.

4. Ved å gi vilkårlige verdier til frie variabler oppnås alle verdiene til hovedvariablene.

Metoder for å løse systemer av lineære ligninger.

Invers matrisemetode.

og , det vil si at systemet har en unik løsning. Vi skriver systemet i matriseform

hvor , , .

Multipliser begge sider av matriseligningen til venstre med matrisen

Siden får vi , hvorfra vi oppnår likhet for å finne ukjente

Eksempel 27. Ved å bruke den inverse matrisemetoden, løs systemet med lineære ligninger

Løsning. Angi med hovedmatrisen til systemet

.

La , så finner vi løsningen ved formelen .

La oss regne ut.

Siden har systemet en unik løsning. Finn alle algebraiske tillegg

, ,

, ,

, ,

, ,

På denne måten

.

La oss sjekke

.

Den inverse matrisen er funnet riktig. Herfra finner vi matrisen av variabler ved å bruke formelen .

.

Ved å sammenligne verdiene til matrisene får vi svaret: .

Cramers metode.

La et system av lineære ligninger med ukjente gis

og , det vil si at systemet har en unik løsning. Vi skriver løsningen av systemet i matriseform eller

Betegn

. . . . . . . . . . . . . . ,

Dermed får vi formler for å finne verdiene til de ukjente, som kalles Cramers formler.

Eksempel 28. Løs følgende system med lineære ligninger ved å bruke Cramers metode .

Løsning. Finn determinanten for hovedmatrisen til systemet

.

Siden da har systemet en unik løsning.

Finn de gjenværende determinantene for Cramers formler

,

,

.

Ved å bruke Cramers formler finner vi verdiene til variablene

Gauss metode.

Metoden består i sekvensiell ekskludering av variabler.

La et system av lineære ligninger med ukjente gis.

Den Gaussiske løsningsprosessen består av to trinn:

På det første trinnet reduseres den utvidede matrisen til systemet til trinnvis form ved hjelp av elementære transformasjoner

,

hvor , som tilsvarer systemet

Etter det variablene regnes som frie og i hver ligning overføres til høyre side.

På det andre trinnet uttrykkes variabelen fra den siste ligningen, den resulterende verdien erstattes i ligningen. Fra denne ligningen

variabel er uttrykt. Denne prosessen fortsetter til den første ligningen. Resultatet er et uttrykk for hovedvariablene i form av de frie variablene .

Eksempel 29. Løs følgende system ved hjelp av Gauss-metoden

Løsning. La oss skrive ut den utvidede matrisen til systemet og redusere den til trinnformen

.

Fordi er større enn antall ukjente, så er systemet kompatibelt og har et uendelig antall løsninger. La oss skrive ned systemet for trinnmatrisen

Determinanten til den utvidede matrisen til dette systemet, sammensatt av de tre første kolonnene, er ikke lik null, så vi anser den som grunnleggende. Variabler

Vil være grunnleggende og variabelen vil være gratis. La oss flytte den i alle ligninger til venstre side

Fra den siste ligningen uttrykker vi

Ved å erstatte denne verdien i den nest siste andre ligningen, får vi

hvor . Ved å erstatte verdiene til variablene og inn i den første ligningen finner vi . Vi skriver svaret i følgende skjema

Et system med lineære ligninger er en forening av n lineære ligninger, som hver inneholder k variabler. Det er skrevet slik:

Mange, når de står overfor høyere algebra for første gang, tror feilaktig at antall ligninger nødvendigvis må falle sammen med antall variabler. I skolealgebra er dette vanligvis tilfelle, men for høyere algebra er dette generelt sett ikke sant.

Løsningen av et likningssystem er en tallrekke (k 1 , k 2 , ..., k n ), som er løsningen til hver likning i systemet, dvs. når du substituerer inn i denne ligningen i stedet for variablene x 1 , x 2 , ..., gir x n den korrekte numeriske likheten.

Følgelig betyr å løse et ligningssystem å finne settet med alle dets løsninger eller å bevise at dette settet er tomt. Siden antall ligninger og antall ukjente kanskje ikke er det samme, er tre tilfeller mulige:

1. Systemet er inkonsekvent, dvs. settet med alle løsninger er tomt. Et ganske sjeldent tilfelle som lett oppdages uavhengig av hvilken metode man skal løse systemet.
2. Systemet er konsistent og definert, d.v.s. har akkurat én løsning. Den klassiske versjonen, velkjent siden skolen.
3. Systemet er konsistent og udefinert, d.v.s. har uendelig mange løsninger. Dette er det vanskeligste alternativet. Det er ikke nok å slå fast at «systemet har et uendelig sett med løsninger» – det er nødvendig å beskrive hvordan dette settet er ordnet.

Variabelen x i kalles tillatt hvis den er inkludert i kun én ligning i systemet, og med koeffisienten 1. Med andre ord, i de resterende ligningene må koeffisienten for variabelen x i være lik null.

Hvis vi velger én tillatt variabel i hver ligning, får vi et sett med tillatte variabler for hele ligningssystemet. Selve systemet, skrevet i denne formen, vil også bli kalt tillatt. Generelt sett kan ett og samme startsystem reduseres til forskjellige tillatte systemer, men dette angår oss ikke nå. Her er eksempler på tillatte systemer:

Begge systemene er tillatt med hensyn til variablene x 1 , x 3 og x 4 . Imidlertid kan det med samme suksess hevdes at det andre systemet er tillatt med hensyn til x 1 , x 3 og x 5 . Det er nok å omskrive den siste ligningen i formen x 5 = x 4 .

Vurder nå mer generell sak. Anta at vi har k variabler totalt, hvorav r er tillatt. Da er to tilfeller mulige:

1. Antall tillatte variabler r er lik det totale antallet variabler k : r = k . Vi får et system med k likninger der r = k tillatte variabler. Et slikt system er samarbeidende og bestemt, fordi x 1 \u003d b 1, x 2 \u003d b 2, ..., x k \u003d b k;
2. Antall tillatte variabler r er mindre enn det totale antallet variabler k : r< k . Остальные (k − r ) переменных называются свободными - они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.

Så i de ovennevnte systemene er variablene x 2 , x 5 , x 6 (for det første systemet) og x 2 , x 5 (for det andre) frie. Tilfellet når det er frie variabler er bedre formulert som et teorem:

Vennligst merk: dette er veldig viktig poeng! Avhengig av hvordan du skriver det endelige systemet, kan den samme variabelen være både tillatt og gratis. De fleste avanserte matteveiledere anbefaler å skrive ut variabler i leksikografisk rekkefølge, dvs. stigende indeks. Du trenger imidlertid ikke følge dette rådet i det hele tatt.

Teorem. Hvis variablene x 1 , x 2 , ..., x r er tillatt i et system med n ligninger, og x r + 1 , x r + 2 , ..., x k er frie, så er:

1. Hvis vi setter verdiene til frie variabler (x r + 1 = t r + 1 , x r + 2 = t r + 2 , ..., x k = t k ), og deretter finner verdiene x 1 , x 2 , . .., x r , vi får en av løsningene.
2. Hvis verdiene til de frie variablene i to løsninger er de samme, er verdiene til de tillatte variablene også de samme, dvs. løsninger er like.

Hva er meningen med dette teoremet? For å få alle løsninger av det tillatte ligningssystemet, er det tilstrekkelig å skille ut de frie variablene. Deretter tilordner du til frie variabler forskjellige betydninger, vil vi motta nøkkelferdige løsninger. Det er alt - på denne måten kan du få alle løsningene til systemet. Det finnes ingen andre løsninger.

Konklusjon: det tillatte likningssystemet er alltid kompatibelt. Hvis antall ligninger i det tillatte systemet er lik antall variabler, vil systemet være bestemt, hvis mindre, vil det være ubestemt.

Og alt ville være bra, men spørsmålet oppstår: hvordan få den løste fra det opprinnelige ligningssystemet? For dette er det

Leksjonens innhold

Lineære ligninger med to variabler

Eleven har 200 rubler for å spise lunsj på skolen. En kake koster 25 rubler, og en kopp kaffe koster 10 rubler. Hvor mange kaker og kopper kaffe kan du kjøpe for 200 rubler?

Angi antall kaker gjennom x, og antall kopper kaffe gjennom y. Da vil prisen på kaker bli betegnet med uttrykket 25 x, og kostnaden for kopper kaffe i 10 y .

25x- pris x kaker
10y- pris y kopper kaffe

Det totale beløpet skal være 200 rubler. Da får vi en ligning med to variabler x og y

25x+ 10y= 200

Hvor mange røtter har denne ligningen?

Alt avhenger av appetitten til studenten. Hvis han kjøper 6 kaker og 5 kopper kaffe, vil røttene til ligningen være tallene 6 og 5.

Verdiparet 6 og 5 sies å være røttene til ligning 25 x+ 10y= 200 . Skrevet som (6; 5) , med det første tallet som verdien av variabelen x, og den andre - verdien av variabelen y .

6 og 5 er ikke de eneste røttene som reverserer ligning 25 x+ 10y= 200 til identitet. Hvis ønskelig, for de samme 200 rubler, kan en student kjøpe 4 kaker og 10 kopper kaffe:

I dette tilfellet, røttene til ligning 25 x+ 10y= 200 er verdiparet (4; 10) .

Dessuten kan en student ikke kjøpe kaffe i det hele tatt, men kjøpe kaker for alle 200 rubler. Deretter røttene til ligning 25 x+ 10y= 200 vil være verdiene 8 og 0

Eller omvendt, ikke kjøp kaker, men kjøp kaffe for alle 200 rubler. Deretter røttene til ligning 25 x+ 10y= 200 vil være verdiene 0 og 20

La oss prøve å liste opp alle mulige røtter til ligning 25 x+ 10y= 200 . La oss være enige om at verdiene x og y tilhører settet med heltall. Og la disse verdiene være større enn eller lik null:

x∈Z, y∈ Z;
x ≥ 0, y ≥ 0

Så det vil være praktisk for studenten selv. Kaker er mer praktisk å kjøpe hele enn for eksempel flere hele kaker og en halv kake. Kaffe er også mer praktisk å ta i hele kopper enn for eksempel flere hele kopper og en halv kopp.

Merk at for oddetall x det er umulig å oppnå likhet under noen y. Så verdiene x det vil være følgende tall 0, 2, 4, 6, 8. Og å vite x kan lett bestemmes y

Dermed fikk vi følgende verdipar (0; 20), (2; 15), (4; 10), (6; 5), (8; 0). Disse parene er løsninger eller røtter til ligning 25 x+ 10y= 200. De gjør denne ligningen til en identitet.

Skriv ligning ax + by = c kalt lineær ligning med to variabler. En løsning eller røttene til denne ligningen er et par verdier ( x; y), som gjør det til en identitet.

Merk også at hvis en lineær ligning med to variabler skrives som ax + b y = c , så sier de at det er skrevet inn kanonisk(normal) form.

Noen lineære ligninger i to variabler kan reduseres til kanonisk form.

For eksempel ligningen 2(16x+ 3y- 4) = 2(12 + 8x − y) kan bringes i tankene ax + by = c. La oss åpne parentesene i begge deler av denne ligningen, får vi 32x + 6y − 8 = 24 + 16x − 2y . Begrepene som inneholder ukjente er gruppert på venstre side av ligningen, og begrepene fri for ukjente er gruppert til høyre. Så får vi 32x - 16x+ 6y+ 2y = 24 + 8 . Vi bringer lignende termer i begge deler, vi får ligning 16 x+ 8y= 32. Denne ligningen er redusert til formen ax + by = c og er kanonisk.

Ligning 25 vurdert tidligere x+ 10y= 200 er også en lineær ligning med to variable i kanonisk form. I denne ligningen, parametrene en , b og c er lik henholdsvis verdiene 25, 10 og 200.

Egentlig ligningen ax + by = c har et uendelig antall løsninger. Løsning av ligningen 25x+ 10y= 200, vi så etter røttene bare på settet med heltall. Som et resultat fikk vi flere verdipar som gjorde denne ligningen til en identitet. Men på settet med rasjonelle tall ligning 25 x+ 10y= 200 vil ha et uendelig antall løsninger.

For å få nye verdipar må du ta en vilkårlig verdi for x, så uttrykk y. La oss for eksempel ta en variabel x verdi 7. Da får vi en likning med én variabel 25×7 + 10y= 200 å uttrykke seg i y

La x= 15. Så ligningen 25x+ 10y= 200 blir 25 × 15 + 10y= 200. Herfra finner vi det y = −17,5

La x= −3 . Så ligningen 25x+ 10y= 200 blir 25 × (−3) + 10y= 200. Herfra finner vi det y = −27,5

System av to lineære ligninger med to variabler

For ligningen ax + by = c du kan ta et hvilket som helst antall ganger vilkårlige verdier for x og finne verdier for y. Sett hver for seg vil en slik likning ha et uendelig antall løsninger.

Men det hender også at variablene x og y ikke forbundet med én, men med to ligninger. I dette tilfellet danner de den såkalte system av lineære ligninger med to variabler. Et slikt ligningssystem kan ha ett verdipar (eller med andre ord: "én løsning").

Det kan også skje at systemet ikke har noen løsninger i det hele tatt. Et system med lineære ligninger kan ha et uendelig antall løsninger i sjeldne og eksepsjonelle tilfeller.

To lineære ligninger danner et system når verdiene x og y er inkludert i hver av disse ligningene.

La oss gå tilbake til den aller første ligningen 25 x+ 10y= 200 . Et av verdiparene for denne ligningen var paret (6; 5) . Dette er tilfellet når 200 rubler kunne kjøpe 6 kaker og 5 kopper kaffe.

Vi komponerer oppgaven slik at paret (6; 5) blir eneste løsning for ligning 25 x+ 10y= 200 . For å gjøre dette, komponerer vi en annen ligning som vil koble den samme x kaker og y kopper kaffe.

La oss sette teksten til oppgaven som følger:

«En skolegutt kjøpte flere kaker og flere kopper kaffe for 200 rubler. En kake koster 25 rubler, og en kopp kaffe koster 10 rubler. Hvor mange kaker og kaffekopper kjøpte eleven hvis man vet at antall kaker er én mer enn antall kopper kaffe?

Vi har allerede den første ligningen. Dette er ligning 25 x+ 10y= 200 . La oss nå skrive en ligning for betingelsen "antall kaker er en enhet mer enn antall kopper kaffe" .

Antall kaker er x, og antall kopper kaffe er y. Du kan skrive denne setningen ved å bruke ligningen x − y= 1. Denne ligningen vil bety at forskjellen mellom kaker og kaffe er 1.

x=y+ 1. Denne ligningen betyr at antall kaker er én mer enn antall kopper kaffe. Derfor, for å oppnå likhet, legges man til antall kopper kaffe. Dette kan lett forstås hvis vi bruker vektmodellen som vi vurderte når vi studerte de enkleste problemene:

Har to ligninger: 25 x+ 10y= 200 og x=y+ 1. Siden verdiene x og y, nemlig 6 og 5 er inkludert i hver av disse ligningene, så danner de sammen et system. La oss skrive ned dette systemet. Hvis ligningene danner et system, er de innrammet av systemets fortegn. Systemtegnet er en krøllete klammeparentes:

La oss bestemme dette systemet. Dette vil tillate oss å se hvordan vi kommer frem til verdiene 6 og 5. Det er mange metoder for å løse slike systemer. Vurder de mest populære av dem.

Substitusjonsmetode

Navnet på denne metoden taler for seg selv. Dens essens er å erstatte en ligning med en annen, etter å ha uttrykt en av variablene tidligere.

I vårt system trenger ingenting å uttrykkes. I den andre ligningen x = y+ 1 variabel x allerede uttrykt. Denne variabelen er lik uttrykket y+ 1. Da kan du erstatte dette uttrykket i den første ligningen i stedet for variabelen x

Etter å ha erstattet uttrykket y+ 1 i den første ligningen i stedet x, får vi ligningen 25(y+ 1) + 10y= 200 . Dette er en lineær ligning med én variabel. Denne ligningen er ganske enkel å løse:

Vi fant verdien av variabelen y. Nå erstatter vi denne verdien i en av ligningene og finner verdien x. For dette er det praktisk å bruke den andre ligningen x = y+ 1. La oss legge verdien inn i det y

Så paret (6; 5) er en løsning på likningssystemet, slik vi hadde tenkt. Vi sjekker og forsikrer oss om at paret (6; 5) tilfredsstiller systemet:

Eksempel 2

Bytt ut den første ligningen x= 2 + y inn i den andre ligningen 3 x - 2y= 9. I den første ligningen, variabelen x er lik uttrykket 2+ y. Vi erstatter dette uttrykket i den andre ligningen i stedet for x

La oss nå finne verdien x. For å gjøre dette, erstatte verdien y inn i den første ligningen x= 2 + y

Så løsningen til systemet er parverdien (5; 3)

Eksempel 3. Løs følgende ligningssystem ved å bruke substitusjonsmetoden:

Her, i motsetning til de foregående eksemplene, er en av variablene ikke eksplisitt uttrykt.

For å erstatte en ligning med en annen, trenger du først .

Det er ønskelig å uttrykke variabelen som har en koeffisient på én. Koeffisientenheten har en variabel x, som er inneholdt i den første ligningen x+ 2y= 11. La oss uttrykke denne variabelen.

Etter et variabelt uttrykk x, vil systemet vårt se slik ut:

Nå erstatter vi den første ligningen med den andre og finner verdien y

Erstatning y x

Så løsningen av systemet er et par verdier (3; 4)

Du kan selvfølgelig også uttrykke en variabel y. Røttene vil ikke endre seg. Men hvis du uttrykker y, Resultatet er ikke en veldig enkel ligning, hvis løsning vil ta mer tid. Det vil se slik ut:

Vi ser det i dette eksemplet for å uttrykke x mye mer praktisk enn å uttrykke y .

Eksempel 4. Løs følgende ligningssystem ved å bruke substitusjonsmetoden:

Uttrykk i den første ligningen x. Da vil systemet ta formen:

y

Erstatning y inn i den første ligningen og finn x. Du kan bruke den opprinnelige ligningen 7 x+ 9y= 8 , eller bruk ligningen der variabelen er uttrykt x. Vi vil bruke denne ligningen, siden den er praktisk:

Så løsningen til systemet er verdiparet (5; −3)

Tilleggsmetode

Addisjonsmetoden er å legge til begrep for ledd likningene som inngår i systemet. Dette tillegget resulterer i en ny envariabelligning. Og det er ganske enkelt å løse denne ligningen.

La oss løse følgende ligningssystem:

Legg til venstre side av den første ligningen til venstre side av den andre ligningen. Og høyre side av den første ligningen med høyre side av den andre ligningen. Vi får følgende likestilling:

Her er lignende termer:

Som et resultat fikk vi den enkleste ligningen 3 x= 27 hvis rot er 9. Å kjenne verdien x du kan finne verdien y. Erstatt verdien x inn i den andre ligningen x − y= 3. Vi får 9 − y= 3. Herfra y= 6 .

Så løsningen av systemet er et par verdier (9; 6)

Eksempel 2

Legg til venstre side av den første ligningen til venstre side av den andre ligningen. Og høyre side av den første ligningen med høyre side av den andre ligningen. I den resulterende likheten presenterer vi slike termer:

Som et resultat fikk vi den enkleste ligningen 5 x= 20, hvor roten er 4. Å kjenne verdien x du kan finne verdien y. Erstatt verdien x inn i den første ligningen 2 x+y= 11. La oss få 8+ y= 11. Herfra y= 3 .

Så løsningen til systemet er verdiparet (4;3)

Tilsetningsprosessen er ikke beskrevet i detalj. Det må gjøres i sinnet. Ved addering må begge ligningene reduseres til kanonisk form. Det er å si ac+by=c .

Fra de betraktede eksemplene kan man se at hovedmålet med å legge til ligninger er å bli kvitt en av variablene. Men det er ikke alltid mulig å umiddelbart løse likningssystemet ved hjelp av addisjonsmetoden. Som oftest bringes systemet foreløpig til en form der det er mulig å legge til likningene som inngår i dette systemet.

For eksempel systemet kan løses direkte ved addisjonsmetoden. Når du legger til begge ligningene, vil begrepene y og −y forsvinne fordi summen deres er null. Som et resultat dannes den enkleste ligningen 11 x= 22 , hvis rot er 2. Da vil det være mulig å bestemme y lik 5.

Og ligningssystemet addisjonsmetoden kan ikke løses umiddelbart, siden dette ikke vil føre til at en av variablene forsvinner. Addisjon vil resultere i ligning 8 x+ y= 28 , som har et uendelig antall løsninger.

Hvis begge deler av ligningen multipliseres eller divideres med samme tall som ikke er lik null, vil en ligning tilsvarende den gitte fås. Denne regelen er også gyldig for et system av lineære ligninger med to variabler. En av ligningene (eller begge ligningene) kan multipliseres med et tall. Resultatet er et ekvivalent system, hvis røtter vil falle sammen med det forrige.

La oss gå tilbake til det aller første systemet, som beskrev hvor mange kaker og kaffekopper studenten kjøpte. Løsningen til dette systemet var et par verdier (6; 5) .

Vi multipliserer begge ligningene som er inkludert i dette systemet med noen tall. La oss si at vi multipliserer den første ligningen med 2 og den andre med 3

Resultatet er et system
Løsningen på dette systemet er fortsatt verdiparet (6; 5)

Dette betyr at likningene som inngår i systemet kan reduseres til en form som egner seg for å anvende addisjonsmetoden.

Tilbake til systemet , som vi ikke kunne løse med addisjonsmetoden.

Multipliser den første ligningen med 6 og den andre med −2

Da får vi følgende system:

Vi legger til ligningene som er inkludert i dette systemet. Tilsetning av komponenter 12 x og -12 x vil resultere i 0, tillegg 18 y og 4 y vil gi 22 y, og å legge til 108 og −20 gir 88. Da får du ligningen 22 y= 88, derfor y = 4 .

Hvis det først er vanskelig å legge til ligninger i tankene dine, kan du skrive ned hvordan venstre side av den første ligningen legges til venstre side av andre ligning, og høyre side av første ligning til høyre side av den andre ligningen:

Å vite at verdien av variabelen y er 4, kan du finne verdien x. Erstatning y inn i en av ligningene, for eksempel inn i den første ligningen 2 x+ 3y= 18. Da får vi en ligning med én variabel 2 x+ 12 = 18. Vi overfører 12 til høyre side, endrer skiltet, vi får 2 x= 6, derfor x = 3 .

Eksempel 4. Løs følgende ligningssystem ved å bruke addisjonsmetoden:

Multipliser den andre ligningen med −1. Da vil systemet ha følgende form:

La oss legge til begge ligningene. Tilsetting av komponenter x og −x vil resultere i 0, tillegg 5 y og 3 y vil gi 8 y, og å legge til 7 og 1 gir 8. Resultatet er ligning 8 y= 8 , hvis rot er 1. Å vite at verdien y er 1, kan du finne verdien x .

Erstatning y inn i den første ligningen, får vi x+ 5 = 7, derav x= 2

Eksempel 5. Løs følgende ligningssystem ved å bruke addisjonsmetoden:

Det er ønskelig at termene som inneholder de samme variablene er plassert under hverandre. Derfor, i den andre ligningen, begrepene 5 y og −2 x bytte plass. Som et resultat vil systemet ta formen:

Multipliser den andre ligningen med 3. Da vil systemet ha formen:

La oss nå legge til begge ligningene. Som et resultat av addisjon får vi ligning 8 y= 16 , hvis rot er 2.

Erstatning y inn i den første ligningen får vi 6 x− 14 = 40 . Vi overfører begrepet −14 til høyre side, endrer tegnet, vi får 6 x= 54. Herfra x= 9.

Eksempel 6. Løs følgende ligningssystem ved å bruke addisjonsmetoden:

La oss bli kvitt brøker. Multipliser den første ligningen med 36 og den andre med 12

I det resulterende systemet den første ligningen kan multipliseres med −5 og den andre med 8

La oss legge til ligningene i det resulterende systemet. Da får vi den enkleste ligningen −13 y= −156 . Herfra y= 12. Erstatning y inn i den første ligningen og finn x

Eksempel 7. Løs følgende ligningssystem ved å bruke addisjonsmetoden:

Vi bringer begge likningene til normal form. Her er det praktisk å bruke proporsjonsregelen i begge ligningene. Hvis høyresiden i den første ligningen er representert som , og høyresiden av den andre ligningen som , vil systemet ha formen:

Vi har en andel. Vi multipliserer dens ekstreme og mellomste termer. Da vil systemet ta formen:

Vi multipliserer den første ligningen med −3, og åpner parentesene i den andre:

La oss nå legge til begge ligningene. Som et resultat av å legge til disse ligningene får vi en likhet, i begge deler vil det være null:

Det viser seg at systemet har et uendelig antall løsninger.

Men vi kan ikke bare ta vilkårlige verdier fra himmelen for x og y. Vi kan spesifisere en av verdiene, og den andre vil bli bestemt avhengig av verdien vi spesifiserer. La for eksempel x= 2 . Bytt inn denne verdien i systemet:

Som et resultat av å løse en av ligningene vil verdien for y, som vil tilfredsstille begge ligningene:

Det resulterende verdiparet (2; −2) vil tilfredsstille systemet:

La oss finne et annet verdipar. La x= 4. Sett inn denne verdien i systemet:

Det kan avgjøres med øyet at y er lik null. Da får vi et par verdier (4; 0), som tilfredsstiller systemet vårt:

Eksempel 8. Løs følgende ligningssystem ved å bruke addisjonsmetoden:

Multipliser den første ligningen med 6 og den andre med 12

La oss skrive om det som er igjen:

Multipliser den første ligningen med −1. Da vil systemet ta formen:

La oss nå legge til begge ligningene. Som et resultat av addisjon dannes ligning 6 b= 48 , hvis rot er 8. Erstatter b inn i den første ligningen og finn en

System av lineære ligninger med tre variabler

En lineær ligning med tre variabler inkluderer tre variabler med koeffisienter, samt et skjæringspunkt. I kanonisk form kan det skrives som følger:

ax + by + cz = d

Denne ligningen har et uendelig antall løsninger. Gir to variabler ulike betydninger, kan du finne den tredje verdien. Løsningen i dette tilfellet er trippelen av verdier ( x; y; z) som gjør ligningen til en identitet.

Hvis variabler x, y, z er forbundet med tre ligninger, så dannes et system med tre lineære ligninger med tre variabler. For å løse et slikt system kan du bruke de samme metodene som gjelder for lineære ligninger med to variabler: substitusjonsmetoden og addisjonsmetoden.

Eksempel 1. Løs følgende ligningssystem ved å bruke substitusjonsmetoden:

Vi uttrykker i den tredje ligningen x. Da vil systemet ta formen:

La oss nå gjøre erstatningen. Variabel x er lik uttrykket 3 − 2y − 2z . Bytt ut dette uttrykket i den første og andre ligningen:

La oss åpne parentesene i begge ligningene og gi lignende termer:

Vi har kommet til et system av lineære ligninger med to variabler. I dette tilfellet er det praktisk å bruke tilleggsmetoden. Som et resultat, variabelen y vil forsvinne og vi kan finne verdien av variabelen z

La oss nå finne verdien y. For dette er det praktisk å bruke ligningen − y+ z= 4. Erstatt verdien z

La oss nå finne verdien x. Til dette er det praktisk å bruke ligningen x= 3 − 2y − 2z . Bytt inn verdiene i den y og z

Dermed er trippelen av verdier (3; −2; 2) løsningen på systemet vårt. Ved å sjekke forsikrer vi oss om at disse verdiene tilfredsstiller systemet:

Eksempel 2. Løs systemet ved addisjonsmetode

La oss legge til den første ligningen med den andre multiplisert med −2.

Hvis den andre ligningen multipliseres med −2, vil den ha formen −6x+ 6y- 4z = −4 . Legg det nå til den første ligningen:

Vi ser at som et resultat av elementære transformasjoner ble verdien av variabelen bestemt x. Det er lik en.

La oss gå tilbake til hovedsystemet. La oss legge til den andre ligningen med den tredje multiplisert med −1. Hvis den tredje ligningen multipliseres med −1, vil den ha formen −4x + 5y − 2z = −1 . Legg det nå til den andre ligningen:

Fikk ligningen x - 2y= −1 . Bytt verdien inn i den x som vi fant tidligere. Så kan vi bestemme verdien y

Vi kjenner nå verdiene x og y. Dette lar deg bestemme verdien z. Vi bruker en av ligningene som er inkludert i systemet:

Dermed er trippelen av verdier (1; 1; 1) løsningen på systemet vårt. Ved å sjekke forsikrer vi oss om at disse verdiene tilfredsstiller systemet:

Oppgaver for å kompilere systemer av lineære ligninger

Oppgaven med å kompilere ligningssystemer løses ved å introdusere flere variabler. Deretter kompileres ligninger basert på betingelsene for problemet. Fra de kompilerte ligningene danner de et system og løser det. Etter å ha løst systemet, er det nødvendig å sjekke om løsningen tilfredsstiller betingelsene for problemet.

Oppgave 1. En Volga-bil forlot byen til kollektivgården. Hun kom tilbake langs en annen vei, som var 5 km kortere enn den første. Totalt kjørte bilen 35 km begge veier. Hvor mange kilometer er hver vei lang?

Løsning

La x- lengden på den første veien, y- lengden på den andre. Hvis bilen kjørte 35 km begge veier, kan den første ligningen skrives som x+ y= 35. Denne ligningen beskriver summen av lengdene på begge veiene.

Det sies at bilen var på vei tilbake langs veien, som var 5 km kortere enn den første. Da kan den andre ligningen skrives som x− y= 5. Denne ligningen viser at forskjellen mellom lengdene på veiene er 5 km.

Eller den andre ligningen kan skrives som x= y+ 5. Vi vil bruke denne ligningen.

Siden variablene x og y i begge ligningene angir det samme tallet, så kan vi danne et system fra dem:

La oss løse dette systemet ved å bruke en av de tidligere studerte metodene. I dette tilfellet er det praktisk å bruke substitusjonsmetoden, siden variabelen i den andre ligningen x allerede uttrykt.

Bytt ut den andre ligningen med den første og finn y

Erstatt den funnet verdien y inn i den andre ligningen x= y+ 5 og finn x

Lengden på den første veien ble angitt med variabelen x. Nå har vi funnet meningen. Variabel x er 20. Så lengden på den første veien er 20 km.

Og lengden på den andre veien ble angitt med y. Verdien av denne variabelen er 15. Så lengden på den andre veien er 15 km.

La oss ta en sjekk. Først, la oss sørge for at systemet er løst riktig:

La oss nå sjekke om løsningen (20; 15) tilfredsstiller betingelsene for problemet.

Det ble sagt at bilen totalt kjørte 35 km begge veier. Vi legger sammen lengdene på begge veiene og forsikrer oss om at løsningen (20; 15) tilfredsstiller denne betingelsen: 20 km + 15 km = 35 km

Neste tilstand: bilen kom tilbake langs en annen vei, som var 5 km kortere enn den første . Vi ser at løsningen (20; 15) også tilfredsstiller denne betingelsen, siden 15 km er kortere enn 20 km ganger 5 km: 20 km − 15 km = 5 km

Ved kompilering av et system er det viktig at variablene angir de samme tallene i alle likninger som inngår i dette systemet.

Så vårt system inneholder to ligninger. Disse ligningene inneholder igjen variablene x og y, som angir de samme tallene i begge ligningene, nemlig lengdene på veier lik 20 km og 15 km.

Oppgave 2. Eik og furusviller ble lastet på plattformen, totalt 300 sviller. Det er kjent at alle eikesviller veide 1 tonn mindre enn alle furusviller. Bestem hvor mange eike- og furusviller det var separat, hvis hver eikesville veide 46 kg, og hver furusville 28 kg.

Løsning

La x eik og y furusviller ble lastet på plattformen. Hvis det var 300 sviller totalt, kan den første ligningen skrives som x+y = 300 .

Alle eikesviller veide 46 x kg, og furu veide 28 y kg. Siden eikesviller veide 1 tonn mindre enn furusviller, kan den andre ligningen skrives som 28y- 46x= 1000 . Denne ligningen viser at masseforskjellen mellom eik og furusviller er 1000 kg.

Tonn er omregnet til kilo fordi massen til eik- og furusviller måles i kilo.

Som et resultat får vi to ligninger som danner systemet

La oss løse dette systemet. Uttrykk i den første ligningen x. Da vil systemet ta formen:

Bytt ut den første ligningen med den andre og finn y

Erstatning y inn i ligningen x= 300 − y og finne ut hva x

Det betyr at 100 eik og 200 furusviller ble lastet på plattformen.

La oss sjekke om løsningen (100; 200) tilfredsstiller betingelsene for problemet. Først, la oss sørge for at systemet er løst riktig:

Det ble sagt at det var 300 sviller totalt. Vi summerer antallet eike- og furusviller og forsikrer oss om at løsningen (100; 200) tilfredsstiller denne betingelsen: 100 + 200 = 300.

Neste tilstand: alle eikesviller veide 1 tonn mindre enn all furu . Vi ser at løsningen (100; 200) også tilfredsstiller denne betingelsen, siden 46 × 100 kg eikesviller er lettere enn 28 × 200 kg furusviller: 5600 kg − 4600 kg = 1000 kg.

Oppgave 3. Vi tok tre stykker av en legering av kobber og nikkel i vektforhold på 2: 1, 3: 1 og 5: 1. Av disse ble et stykke som veide 12 kg smeltet sammen med et forhold mellom kobber og nikkelinnhold på 4:1. Finn massen til hvert originalstykke hvis massen til den første av dem er to ganger massen til den andre.

System av m lineære ligninger med n ukjente kalt et formsystem

hvor aij og b i (Jeg=1,…,m; b=1,…,n) er noen kjente tall, og x 1,...,x n- ukjent. I notasjonen av koeffisientene aij første indeks Jeg angir tallet på ligningen, og den andre j er tallet på den ukjente som denne koeffisienten står på.

Koeffisientene for de ukjente vil bli skrevet i form av en matrise , som vi vil kalle systemmatrise.

Tallene på høyre side av ligningene b 1,...,b m kalt gratis medlemmer.

Samlet n tall c 1,...,c n kalt beslutning av dette systemet, hvis hver likning i systemet blir en likhet etter å ha erstattet tall i den c 1,...,c n i stedet for de tilsvarende ukjente x 1,...,x n.

Vår oppgave blir å finne løsninger på systemet. I dette tilfellet kan tre situasjoner oppstå:

Et system med lineære ligninger som har minst én løsning kalles ledd. Ellers, dvs. hvis systemet ikke har noen løsninger, kalles det uforenlig.

Vurder måter å finne løsninger på systemet.

MATRISKEMETODE FOR LØSE SYSTEMER AV LINEÆRE LIGNINGER

Matriser gjør det mulig å kort skrive ned et system med lineære ligninger. La et system med 3 ligninger med tre ukjente gis:

Vurder matrisen til systemet og matrisekolonner med ukjente og gratis medlemmer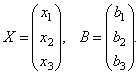

La oss finne produktet

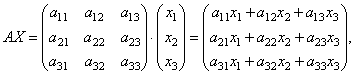
de. som et resultat av produktet får vi venstre side av likningene til dette systemet. Deretter, ved å bruke definisjonen av matriselikhet, kan dette systemet skrives som

eller kortere EN∙X=B.

Her matriser EN og B er kjent, og matrisen X ukjent. Hun må bli funnet, fordi. dens elementer er løsningen på dette systemet. Denne ligningen kalles matriseligning.

La matrisedeterminanten være forskjellig fra null | EN| ≠ 0. Da løses matriseligningen som følger. Multipliser begge sider av ligningen til venstre med matrisen A-1, den inverse av matrisen EN: . Fordi det A -1 A = E og E∙X=X, så får vi løsningen av matriseligningen på formen X = A -1 B .

Merk at siden den inverse matrisen bare kan finnes for kvadratiske matriser, kan matrisemetoden bare løse de systemene der antall ligninger er det samme som antall ukjente. Imidlertid er matrisenotasjonen til systemet også mulig i tilfellet når antall ligninger ikke er lik antall ukjente, da er matrisen EN er ikke firkantet og derfor er det umulig å finne en løsning på systemet i skjemaet X = A -1 B.

Eksempler. Løse ligningssystemer.

CRAMERS REGEL

Tenk på et system med 3 lineære ligninger med tre ukjente:

Tredjeordens determinant som tilsvarer matrisen til systemet, dvs. sammensatt av koeffisienter ved ukjente,

kalt systemdeterminant.

Vi komponerer ytterligere tre determinanter som følger: vi erstatter suksessivt 1, 2 og 3 kolonner i determinanten D med en kolonne med frie medlemmer

Da kan vi bevise følgende resultat.

Teorem (Cramers regel). Hvis determinanten for systemet er Δ ≠ 0, så har systemet som vurderes én og bare én løsning, og

Bevis. Så, tenk på et system med 3 ligninger med tre ukjente. Multipliser den første ligningen i systemet med det algebraiske komplementet A 11 element en 11, 2. ligning - på A21 og 3. - på A 31:

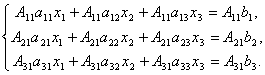
La oss legge til disse ligningene:

Vurder hver av parentesene og høyre side av denne ligningen. Ved teoremet om utvidelse av determinanten når det gjelder elementene i 1. kolonne

På samme måte kan det vises at og .

Til slutt er det lett å se det

Dermed får vi likheten: .

Følgelig.

Likhetene og er avledet på samme måte, hvorfra påstanden om teoremet følger.

Dermed legger vi merke til at hvis determinanten til systemet er Δ ≠ 0, så har systemet en unik løsning og omvendt. Hvis determinanten til systemet er lik null, så har systemet enten et uendelig sett med løsninger eller har ingen løsninger, dvs. uforenlig.

Eksempler. Løs et ligningssystem

GAUSS-METODEN

De tidligere vurderte metodene kan brukes til å løse bare de systemene der antall ligninger sammenfaller med antall ukjente, og determinanten til systemet må være forskjellig fra null. Gaussmetoden er mer universell og passer for systemer med et hvilket som helst antall ligninger. Den består i suksessiv eliminering av ukjente fra systemets ligninger.

Vurder igjen et system med tre ligninger med tre ukjente:

.

Vi lar den første ligningen være uendret, og fra den 2. og 3. ekskluderer vi begrepene som inneholder x 1. For å gjøre dette deler vi den andre ligningen med en 21 og gang med - en 11 og legg til med 1. ligning. På samme måte deler vi den tredje ligningen inn i en 31 og gang med - en 11 og legg den deretter til den første. Som et resultat vil det opprinnelige systemet ha formen:

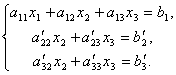
Nå, fra den siste ligningen, eliminerer vi begrepet som inneholder x2. For å gjøre dette, del den tredje ligningen med , multipliser med og legg den til den andre. Da vil vi ha et ligningssystem:

Derfor er det lett å finne den fra den siste ligningen x 3, deretter fra 2. ligning x2 og til slutt fra 1. x 1.

Ved bruk av Gauss-metoden kan likningene byttes om nødvendig.

Ofte, i stedet for å skrive et nytt ligningssystem, begrenser de seg til å skrive ut den utvidede matrisen til systemet:

og deretter bringe den til en trekantet eller diagonal form ved hjelp av elementære transformasjoner.

Til elementære transformasjoner matriser inkluderer følgende transformasjoner:

1. permutasjon av rader eller kolonner;
2. multiplisere en streng med et tall som ikke er null;
3. legge til andre linjer på en linje.

Eksempler: Løs ligningssystemer ved hjelp av Gauss-metoden.

Dermed har systemet et uendelig antall løsninger.