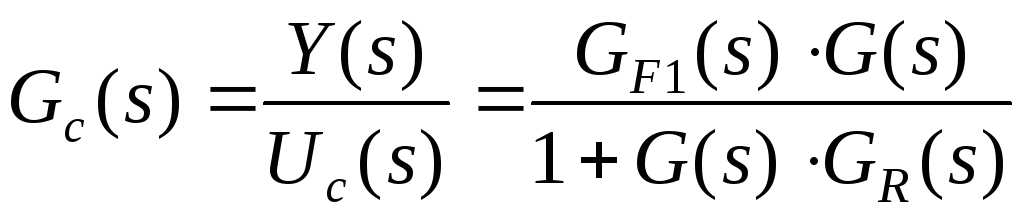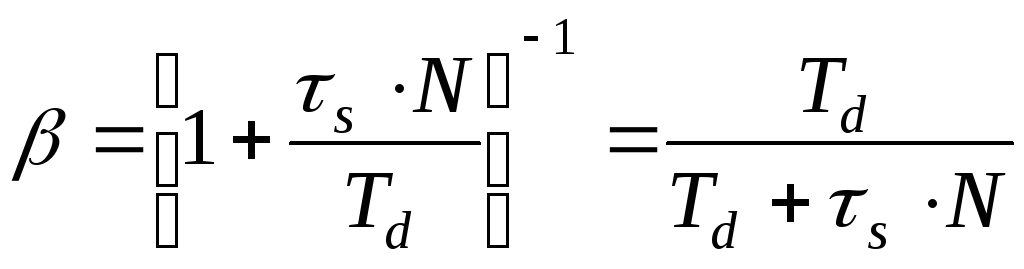Enkel diskret PID-kontrolleralgoritme

Støttes av alle AVR-mikrokontrollere

PID-funksjonen bruker 534 byte med flashminne og 877 prosessorsykluser (IAR - lavstørrelsesoptimalisering)

1. Introduksjon

Denne håndboken beskriver en enkel implementering av en diskret proporsjonal-integral-derivert (PID) kontroller.

Ved arbeid med applikasjoner hvor systemets utgangssignal må endres i henhold til referanseverdien, kreves det en kontrollalgoritme. Eksempler på slike applikasjoner er en motorkontrollenhet, en kontrollenhet for temperatur, trykk, væskestrøm, hastighet, kraft eller andre variabler. PID-regulatoren kan brukes til å kontrollere enhver målt variabel.

Mange løsninger har vært brukt innen kontroll i lang tid, men PID-regulatorer kan bli "industristandarden" på grunn av sin enkelhet og gode ytelse.

Å motta tilleggsinformasjon for PID-kontrollere og deres applikasjoner bør leseren henvise til andre kilder, for eksempel PID-kontrollere av K. J. Astrom & T. Hagglund (1995)

Figur 1-1. Typiske svar fra en PID-kontroller på en trinnvis endring i referansesignalet

2. PID-kontroller

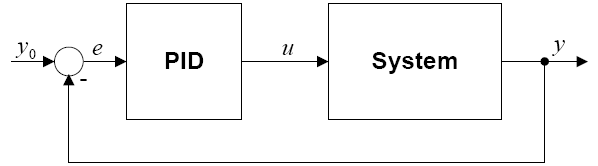
Figur 2-1 viser et diagram over et system med en PID-regulator. PID-regulatoren sammenligner den målte prosessverdien Y med en gitt referanseverdi Y0. Forskjellen, eller feilen, E, behandles deretter for å beregne en ny inndataprosess, U. Denne nye inndataprosessen vil forsøke å bringe verdien av den målte prosessen nærmere den spesifiserte verdien.

Et alternativ til et lukket sløyfestyringssystem er et åpent sløyfestyringssystem. En åpen kontrollsløyfe (uten tilbakemelding) er i mange tilfeller ikke tilfredsstillende, og bruken av den er ofte umulig på grunn av systemets egenskaper.

Figur 2-1. PID lukket sløyfe kontrollsystem

I motsetning til enkle kontrollalgoritmer, er en PID-kontroller i stand til å kontrollere en prosess basert på dens historie og endringshastighet. Dette gir en mer nøyaktig og stabil kontrollmetode.

Hovedideen er at kontrolleren mottar informasjon om tilstanden til systemet ved hjelp av en sensor. Den trekker deretter den målte verdien fra referanseverdien for å beregne feilen. Feilen vil bli håndtert på tre måter: håndtere nåtiden med proporsjonalleddet, gå tilbake til fortiden ved å bruke integralleddet, og forutse fremtiden ved å bruke differensialleddet.

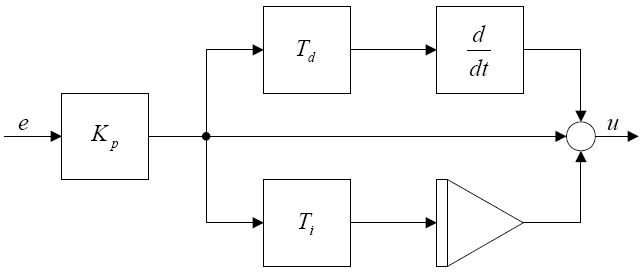
Figur 2-2 viser kretsskjemaet til en PID-kontroller, der Tp, Ti og Td er henholdsvis proporsjonale, integrale og deriverte tidskonstanter.

Figur 2-2. PID-kontrollerdiagram

2.1 Proporsjonal

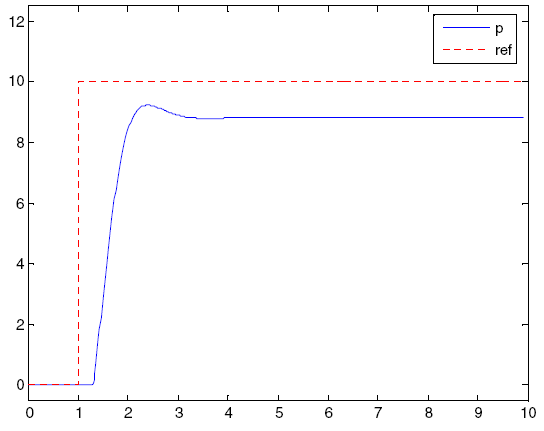
Det proporsjonale leddet (P) gir et styresignal proporsjonalt med den beregnede feilen. Bruk av kun én proporsjonal kontroll gir alltid en stasjonær feil, bortsett fra når styresignalet er null og verdien av systemprosessen er lik den nødvendige verdien. På fig. 2-3 vises en stasjonær feil i verdien av systemprosessen etter en endring i referansesignalet (ref). Bruk av for stor P-term vil gi et ustabilt system.

Figur 2-3. P-kontrollerens respons på en trinnendring i referansesignalet

2.2 Integrert ledd

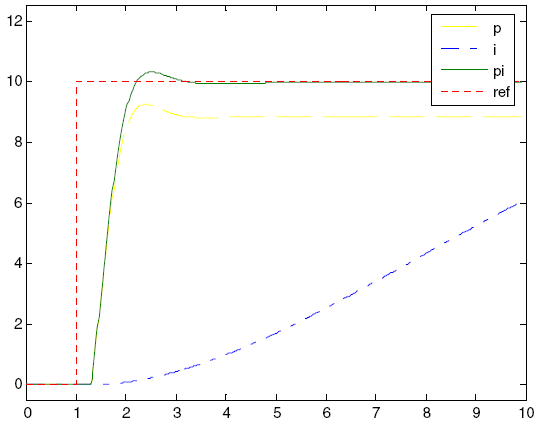
Integralkomponenten (I) representerer de tidligere feilene. Summen av feilen vil fortsette til verdien av systemprosessen blir lik ønsket verdi. Vanligvis brukes integralkomponenten sammen med proporsjonalkomponenten, i de såkalte PI-regulatorene. Bruk av kun den integrerte komponenten gir en langsom respons og ofte et oscillerende system. Figur 2-4 viser trinnresponsen til I- og PI-kontrollerne. Som du kan se, har responsen til PI-kontrolleren ingen stasjonær feil, og responsen til I-kontrolleren er veldig treg.

Figur 2-4. Responsen til I- og PI-kontrolleren på en trinnvis endring i den kontrollerte verdien

2.3 Avledet begrep

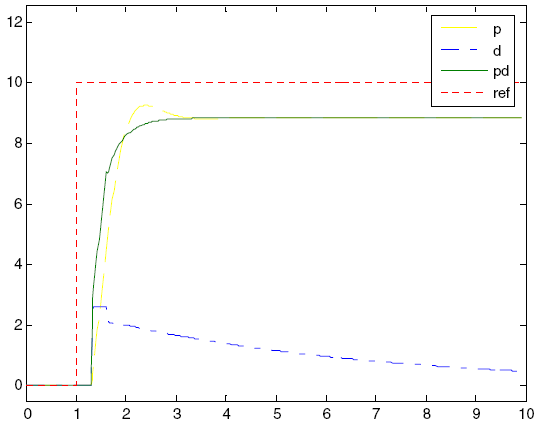
Differensialleddet (D) er endringshastigheten for feilen. Tilsetningen av denne komponenten forbedrer systemets respons på en plutselig endring i tilstanden. Differensialbegrepet D brukes vanligvis med P- eller PI-algoritmer, som PD- eller PID-kontrollere. En stor differensialkomponent D gir vanligvis et ustabilt system. Figur 2-5 viser responsene til D- og PD-kontrolleren. Responsen til PD-regulatoren gir en raskere økning i prosessverdi enn P-regulatoren. Merk at differensialleddet D oppfører seg i hovedsak som et høypassfilter for feilsignalet og dermed lett gjør systemet ustabilt og mer mottakelig for støy.

Figur 2-5. Respons fra D- og PD-kontrolleren på en trinnendring i referansesignalet

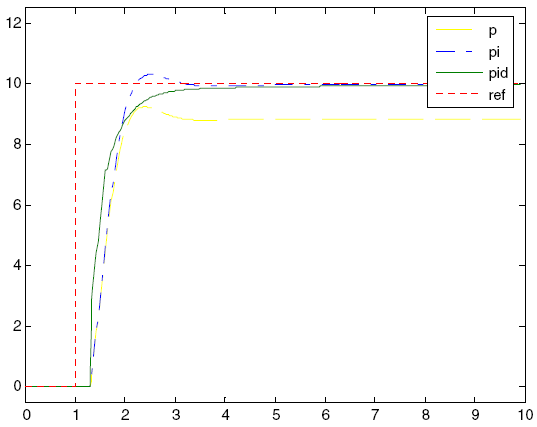
PID-kontrolleren gir best ytelse fordi den bruker alle komponentene sammen. Figur 2-6 sammenligner P-, PI- og PID-kontrollere. PI forbedrer P ved å fjerne den stasjonære feilen, og PID forbedrer PI med raskere respons.

Figur 2-6. P-, PI- og PID-regulatorens respons på en trinnendring i referansesignalet

2.4. Innstillinger

Den beste måten å finne de nødvendige parametrene til PID-algoritmen på er å bruke en matematisk modell av systemet. Imidlertid er det ofte ingen detaljert matematisk beskrivelse av systemet, og innstillingene til PID-regulatorens parametere kan bare gjøres eksperimentelt. Å finne parametere for en PID-kontroller kan være en skremmende oppgave. Her veldig viktig ha data om egenskapene til systemet og ulike forhold hennes arbeid. Noen prosesser bør ikke tillate at prosessvariabelen overskrider settpunktet. Andre prosesser bør minimere energiforbruket. Også det viktigste kravet er stabilitet. Prosessen bør ikke svinge under noen omstendigheter. I tillegg må stabilisering skje innen en viss tid.

Det finnes noen metoder for å stille inn PID-kontrolleren. Valget av metode vil i stor grad avhenge av om prosessen kan være offline for tuning eller ikke. Ziegler-Nichols-metoden er en velkjent ikke-offline tuning-metode. Det første trinnet i denne metoden er å sette I- og D-forsterkningen til null, og øke P-forsterkningen til en jevn og stabil oscillasjon (så nært som mulig). Deretter registreres den kritiske forsterkningen Kc og oscillasjonsperioden Pc og P-, I- og D-verdiene korrigeres ved hjelp av Tabell 2-1.

Tabell 2-1. Beregning av parametere etter Ziegler-Nichols metode

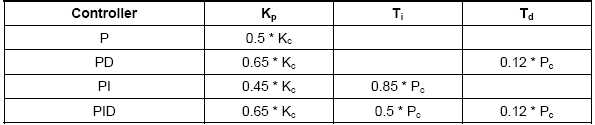
Ytterligere parameterinnstilling er ofte nødvendig for å optimalisere ytelsen til en PID-kontroller. Leseren bør merke seg at det er systemer der en PID-kontroller ikke vil fungere. Dette kan være ikke-lineære systemer, men generelt oppstår det ofte problemer med PID-styring når systemene er ustabile og effekten av inngangssignalet avhenger av systemets tilstand.

2.5. Diskret PID-kontroller

Den diskrete PID-regulatoren vil lese feilen, beregne og sende ut styresignalet for prøvetakingstiden T. Samplingstiden må være mindre enn den minste tidskonstanten i systemet.

2.5.1. Beskrivelse av algoritmen

I motsetning til enkle kontrollalgoritmer, er PID-kontrolleren i stand til å manipulere kontrollsignalet basert på historien og endringshastigheten til det målte signalet. Dette gir en mer nøyaktig og stabil kontrollmetode.

Figur 2-2 viser kretsdesignet til PID-kontrolleren, der Tp, Ti og Td er henholdsvis proporsjonale, integrale og deriverte tidskonstanter.

Overføringsfunksjonen til systemet vist i figur 2-2 er:

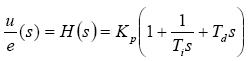
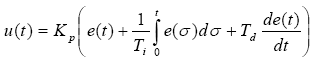
Vi tilnærmer de integrale og differensielle komponentene for å oppnå en diskret form

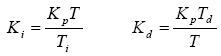
For å unngå at denne endringen i referanseprosessverdien gjør enhver uønsket rask endring på kontrollinngangen, forbedrer kontrolleren kun basert på den avledede termen på prosessverdiene:

3. Implementering av en PID-kontroller i C

En fungerende C-applikasjon er vedlagt dette dokumentet. En fullstendig beskrivelse av kildekoden og kompilasjonsinformasjon finnes i filen "readme.html".

Figur 3-1. Flytskjema for demoapplikasjoner

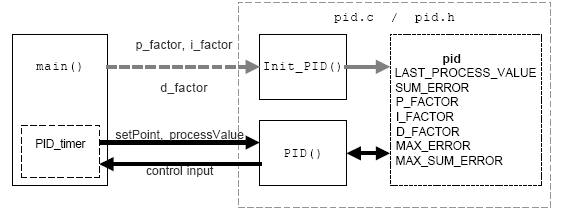
Figur 3-1 viser et forenklet diagram av demoapplikasjonen.

PID-kontrolleren bruker en struktur for å lagre status og parametere. Denne strukturen initialiseres av hovedfunksjonen, og bare en peker til den sendes til funksjonene Init_PID() og PID().

PID()-funksjonen må kalles for hvert tidsintervall T, dette settes av en timer som setter PID_timer-flagget når prøvetiden har gått. Når PID_timer-flagget er satt, leser hovedprogrammet prosessreferanseverdien og prosesssystemverdien, kaller PID()-funksjonen og sender resultatet til kontrollinngangen.

For å øke nøyaktigheten økes p_factor, i_factor og d_factor med 128 ganger. Resultatet av PID-algoritmen reduseres senere ved å dele på 128. Verdien på 128 brukes for å gi en kompileringsoptimalisering.

I tillegg vil påvirkningen av Ifactor og Dfactor avhenge av tiden T.

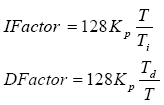
3.1. Integrert avvikling

Når inngangsprosessen, U, når en høy nok verdi, blir den avgrenset. Enten av det interne numeriske området til PID-kontrolleren, eller av utgangsområdet til kontrolleren, eller undertrykt i forsterkerne. Dette vil skje hvis det er stor nok forskjell mellom målt verdi og referanseverdi, vanligvis fordi prosessen har flere forstyrrelser enn systemet er i stand til å håndtere.

Hvis kontrolløren bruker en integrert term, kan denne situasjonen være problematisk. I en slik situasjon vil integralbegrepet hele tiden legge seg opp, men i fravær av store brudd vil PID-kontrolleren begynne å kompensere prosessen til integralsummen går tilbake til normalen.

Dette problemet kan løses på flere måter. I dette eksemplet er den maksimale integralsummen begrenset og kan ikke være større enn MAX_I_TERM. Riktig størrelse MAX_I_TERM vil avhenge av systemet.

4. Videreutvikling

PID-kontrolleren som presenteres her er et forenklet eksempel. Kontrolleren skal fungere bra, men noen applikasjoner kan kreve at kontrolleren er enda mer pålitelig. Det kan være nødvendig å legge til en metningskorrigering i integralleddet, basert på proporsjonalleddet kun på prosessverdien.

I beregningen av Ifactor og Dfactor er samplingstiden T en del av ligningen. Hvis prøvetakingstiden T som brukes er mye mindre enn eller større enn 1 sekund, vil nøyaktigheten til enten Ifactor eller Dfactor være utilstrekkelig. Det er mulig å omskrive PID og skaleringsalgoritmen slik at nøyaktigheten til integral- og differensialleddene bevares.

5. Referanselitteratur

K. J. Astrom & T. Hagglund, 1995: PID-kontrollere: teori, design og tuning.
International Society for Measurement and Con.

6. Filer

AVR221.rar

Oversatt av Kirill Vladimirov på forespørsel

Forelesning 30Implementering av PID-kontroller og digital filtrering i kontrollere

Mikroprosessorkontrollere gjør det mulig å implementere både diskrete og analoge kontrollere, samt ikke-lineære og selvjusterende kontrollere. Hovedproblemet med digital kontroll er å finne den passende strukturen til kontrolleren og dens parametere. Programvareimplementeringen av kontrollalgoritmer for disse parameterne er vanligvis en relativt enkel oppgave.

Hver regulator må også inkludere beskyttelsesmidler som forhindrer den farlige utviklingen av prosessen under påvirkning av regulatoren i nødssituasjoner.

Mange TP-er er preget av flere inngangs- og utgangsparametere. Ofte er de interne forbindelsene og interaksjonen mellom de respektive signalene ikke kritiske, og prosessen kan styres med et sett med enkle kontrollere, hvor hver sløyfe brukes i direkte digitale kontrollsystemer.

Lineære regulatorer med én inngang/utgang kan representeres i en generalisert form

hvor u er kontrollerens utgang (kontrollvariabel), u Med er den innstilte verdien, og på– prosessutgangssignal (styrt variabel). Parameter P representerer rekkefølgen til regulatoren.

En vanlig PID-regulator kan betraktes som et spesialtilfelle av en generalisert diskret kontroller med P= 2.

Tenk på en regulator som består av to deler: en tilbakemeldingssløyfe (tilbakemelding) G Facebook (s) som håndterer feilen E , og fremkoblingssløyfe G FF (s), som kontrollerer endringer i innstillingshandlingen og legger til en korreksjonsterm til kontrollsignalet slik at systemet reagerer raskere på endringer i innstillingen. For denne kontrolleren, kontrollhandlingen U (s ) er summen av to signaler

Dette uttrykket kan skrives om som

hvor U F 1 (s) er et forebyggende signal basert på referanseverdien (innstillingshandling), en U F 2 (s) er et tilbakemeldingssignal.

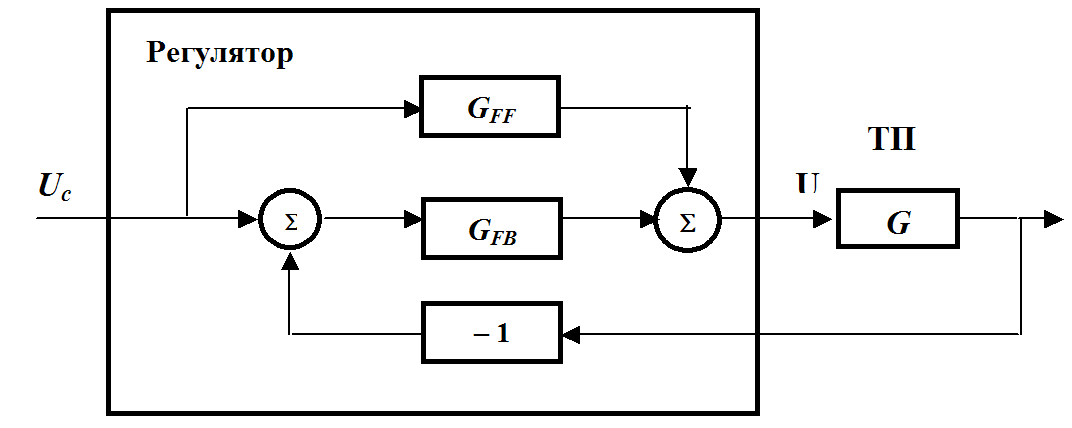
Fig.30.1.En kontroller som inneholder en fremkoblingssløyfe basert på en referanseverdi (settpunkt) og en tilbakekoblingssløyfe basert på prosessutgangen en

Kontrolleren har to inngangssignaler U c (s) og Y(s) og kan derfor beskrives med to overføringsfunksjoner G F 1 (s) og G R (s).

Siden kontrolleren med PF (30.3) har pga G F 1 (s) flere justerbare koeffisienter enn en konvensjonell regulator, da har det lukkede kontrollsystemet bedre egenskaper.

Posisjonen til polene til tilbakemeldingssystemet kan endres ved hjelp av regulatoren G R (s), og feedforward-kontrolleren G F 1 (s) legger til nye nuller til systemet. Derfor kan kontrollsystemet raskt reagere på endringer i oppgavesignalet hvis G F 1 (s) er valgt riktig.

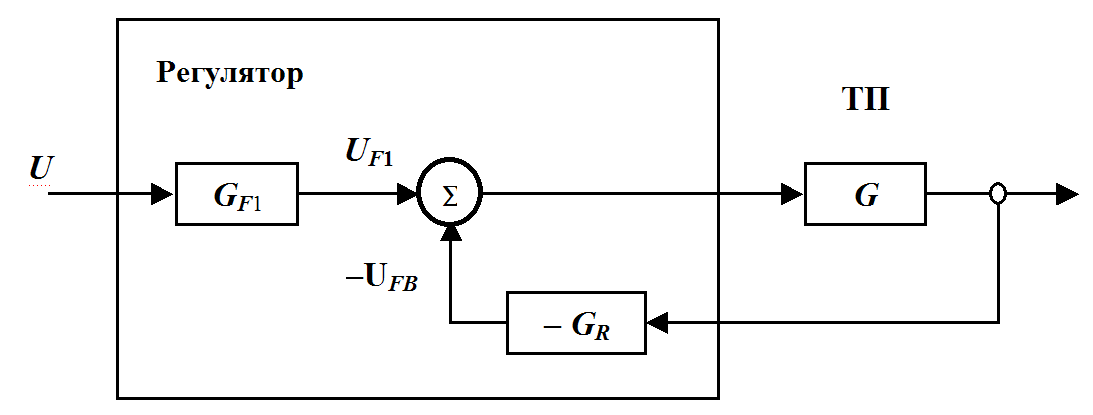
Fig.30.2. Struktur av en lineær regulator med feedforward kontroll og tilbakemelding

Takket være bruken av en slik kontroller er det mulig å lage høypresisjons (servo) kontrollsystemer ved hjelp av elektriske stasjoner, roboter eller maskinverktøy. For dem er det viktig at responsen på prosessutgangen er rask og nøyaktig for enhver endring i referansen.

Hvis telleren og nevneren til PF G R (s), og G F 1 (s) i (23.3) for å uttrykkes med polynomer i s , så kan beskrivelsen av kontrolleren etter transformasjoner representeres i følgende form

G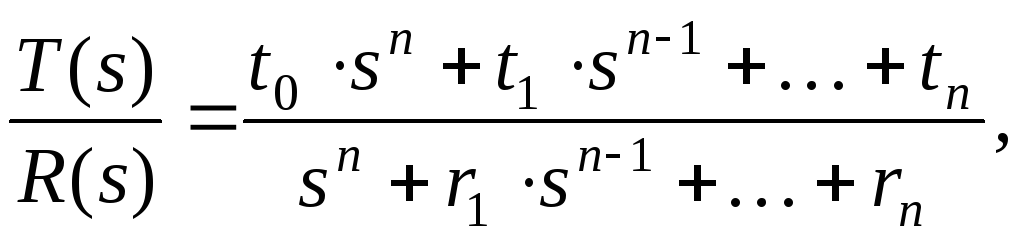



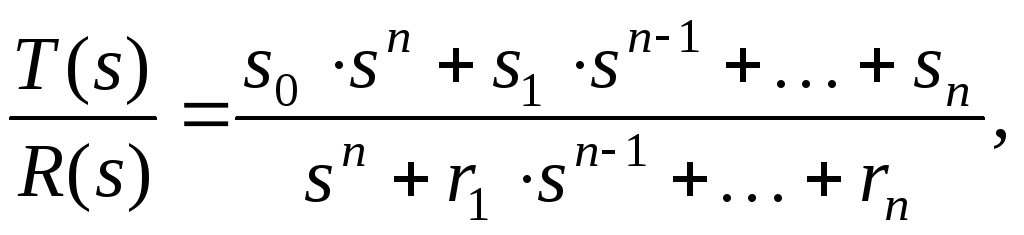de

r Jeg ,s Jeg ,t Jeg – parametere for PF polynomer, s– Laplace-operatør.

Kontrolleren som tilsvarer ligning (30.4) kan representeres som en generalisert kontroller (generell kontroller)

PF av prosessen kan uttrykkes som

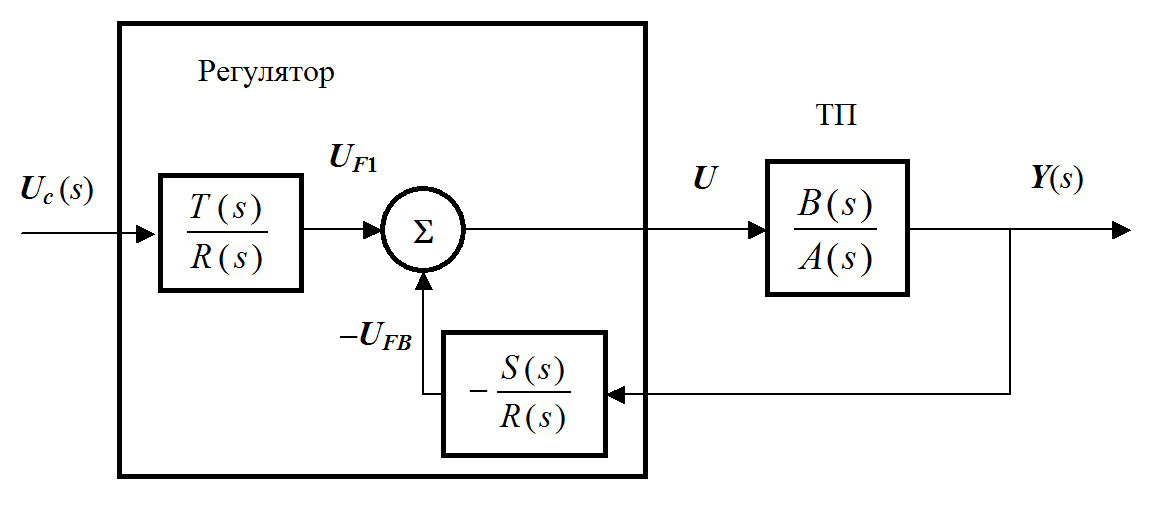
Fig.30.3. Strukturen til en lineær kontroller med feedforward kontroll og tilbakemelding i form av en PF

Hvis R(s),S(s) og T(s) har en tilstrekkelig høy orden, dvs. et tilstrekkelig antall "avstemningsknotter", kan PF til et lukket system varieres over et bredt område. Regulator rekkefølge P må være den samme som den opprinnelige prosessen. Ja, plukker R(s) og S(s), kan man vilkårlig endre nevneren til PF i et lukket system. Teoretisk betyr dette at polene til et lukket system kan flyttes til et hvilket som helst sted i det komplekse planet. (I praksis begrenser den maksimale amplituden og endringshastigheten til styresignalet bevegelsesfriheten til polene.)

Som et resultat kan et ustabilt system med en pol med en positiv reell del stabiliseres ved hjelp av SU.

30.1. Implementering av PID-kontroller

Først av alt bør en diskret kontrollermodell utvikles og en passende samplingsfrekvens bestemmes. Amplituden til utgangsverdien til regulatoren må være mellom minimum og maksimum tillatte verdier. Ofte er det nødvendig å begrense ikke bare utgangssignalet, men også endringshastigheten på grunn av de fysiske egenskapene til MI-ene og for å forhindre overdreven slitasje.

Endring av parameterinnstillinger og overgang fra automatisk til manuell drift eller andre endringer i driftsforhold må ikke føre til forstyrrelser i den kontrollerte prosessen.

Regulatorer kan lages i analog teknologi basert på operasjonsforsterkere eller som digitale enheter basert på mikroprosessorer. Imidlertid har de nesten samme utseende - en liten robust kasse som tillater installasjon i et industrielt miljø.

Mens digital teknologi har mange fordeler, er den analoge tilnærmingen grunnlaget for digitale løsninger. Fordelene med digitale kontrollere inkluderer muligheten til å koble dem til hverandre ved hjelp av kommunikasjonskanaler, som tillater datautveksling og fjernkontroll. Vi er interessert i programmer for en digital PID-kontroller

Diskret PID-kontrollermodell . Det er nødvendig for programvareimplementeringen av den analoge kontrolleren. Hvis kontrolleren er designet på grunnlag av en analog beskrivelse, og deretter dens diskrete modell bygges, med tilstrekkelig små samplingsintervaller, erstattes tidsderiverte med endelige forskjeller, og integrasjon erstattes av summering. Prosessutgangsfeil beregnes for hver prøve

e(k)=u c (k) – y(k) .

I dette tilfellet vil samplingsintervallet t s regnes som konstant, og eventuelle signalendringer som kan ha kommet opp i løpet av prøvetakingsintervallet tas ikke i betraktning.

Det finnes to typer PID-kontrolleralgoritmer - posisjonell og inkrementell

Posisjonell PID-kontrolleralgoritme. I posisjonsalgoritmen ( stilling form) utgangssignalet er den absolutte verdien av kontrollvariabelen IM. Den diskrete PID-kontrolleren har skjemaet

u(k)=u 0 +u P (k)+u Jeg (k)+u D (k).

I dette tilfellet regnes samplingsintervallet ts som konstant, og eventuelle endringer i signalet som kan komme opp i løpet av samplingsintervallet tas ikke i betraktning.

Selv med null kontrollfeil, er utgangssignalet ikke-null og bestemmes av offset u 0 .

Den proporsjonale delen av kontrolleren har formen

u P (k)= K∙ e(k).

Den integrerte delen tilnærmes ved endelige forskjeller

u Jeg (k) = u Jeg (k – 1) + K∙ (t s / T Jeg) ∙ e(k)= u Jeg (k – 1) + K∙ en∙ e(k).

Verdien av den andre termen er liten t s og stor T Jeg kan bli svært liten, så du må sikre den nødvendige nøyaktigheten til maskinrepresentasjonen.

Differensialdelen av PID-kontrolleren tilnærmes ved bakoverforskjellen

u D (k) =b∙ u D (k – 1) – K∙ (T d / t s) ∙ (1– b)∙ [y(k)– y(k – 1)],

Verdi T d / N = T f er den normaliserte N ganger) filtertidskonstanten i tilnærmingen til differensialkomponenten til kontrollloven ved en aperiodisk kobling av første orden. Antall N tatt i området fra 5 til 10. Verdien b er i området fra 0 til 1.

inkrementalgoritme. Den beregner bare endringen i utgangssignalet. Inkrement algoritme ( trinnvis form) PID-kontrolleren er praktisk å bruke hvis IM er en slags integrator, for eksempel en trinnmotor. Et annet eksempel på en slik MI er en ventil hvis åpning og lukking styres av impulser og som opprettholder sin posisjon i fravær av inngangssignaler.

I inkrementalgoritmen er det bare endringer i kontrollutgangssignalet fra tidspunktet ( k – 1) til øyeblikket k. Kontrolleralgoritmen skrives som

Δ u Jeg (k) = u (k) – u (k – 1) =Δ u P (k) + Δ u Jeg (k) + Δ u D (k).

Den proporsjonale delen av inkrementalgoritmen beregnes fra ligningen

Δ u P (k) = u P (k) – u P (k – 1) =K∙ [e(k)– e(k – 1)] = K∙ Δ e(k).

Integrert del - fra ligningen

Δ u Jeg (k) = u Jeg (k) – u Jeg (k – 1) =K∙ en∙ e(k).

Differensialdelen er fra ligningen

Δ u D (k) =b Δ u D (k – 1) – K∙ (T d / t s)∙(1– b)∙ [Δ y(k)– Δ y(k – 1),

Δ y(k) =y(k)– y(k – 1).

Algoritmen er veldig enkel. For dens anvendelse er som regel operasjoner med et flytende punkt med vanlig presisjon tilstrekkelig. Den har ikke problemer på grunn av metning. Når du bytter fra manuell modus til en automatisk regulator som beregner inkrementer, krever det ikke å tildele en startverdi til styresignalet ( u 0 i posisjonsalgoritmen).

IM kan bringes til ønsket posisjon under oppstart både med manuell og automatisk styring. En liten ulempe med inkrementalgoritmen er behovet for å ta hensyn til den integrerte komponenten.

Referanseverdien reduseres både i proporsjonal- og differensialdelen fra den andre prøven etter at den er endret. Derfor, hvis en kontroller basert på en inkrementell algoritme uten en integrert komponent brukes, kan den kontrollerte prosessen avvike fra referanseverdien.

Bestemme samplingsfrekvensen i SN . Det er mer en kunst enn en vitenskap. For lav prøvetakingshastighet reduserer effektiviteten av kontrollen, spesielt kontrollsystemets evne til å kompensere for forstyrrelser. Men hvis prøvetakingsintervallet overskrider prosessens responstid, kan forstyrrelsen påvirke prosessen og forsvinne før kontrolleren tar korrigerende tiltak. Derfor, når du bestemmer prøvetakingshastigheten, er det viktig å ta hensyn til både dynamikken i prosessen og egenskapene til forstyrrelsen.

På den annen side fører for høy samplingsfrekvens til økt datamaskinbelastning og IM-slitasje.

Dermed er bestemmelsen av samplingsfrekvensen et kompromiss mellom kravene til prosessdynamikk og tilgjengelig ytelse til datamaskiner og teknologiske mekanismer. Standard digitale kontrollere som opererer med et lite antall kontrollsløyfer (8 til 16) bruker en fast samplingshastighet i størrelsesorden brøkdeler av et sekund.

Signal-til-støy-forholdet påvirker også samplingshastigheten. Ved lave verdier av dette forholdet, dvs. ved høy støy, bør en høy samplingshastighet unngås, fordi avvik i målesignalet er mer sannsynlig å være assosiert med høyfrekvent støy, og ikke med reelle endringer i den fysiske prosessen.

En adekvat samplingshastighet anses å være relatert til båndbredden eller innreguleringstiden til kontrollsystemet med lukket sløyfe. Tommelfingerregler anbefaler at samplingsfrekvensen er 6-10 ganger høyere enn båndbredden, eller at settlingstiden er minst fem samplingsintervaller.

I tilfelle en ekstra faseforsinkelse på 5-15° er akseptabel, er følgende regel gyldig

t s · ω Med = 0,15 – 0,5 ,

hvor ω Med – systembåndbredde (på 3 dB nivå), t s – kvantiseringsperiode, eller samplingsintervall. (Denne tilnærmingen brukes i mange industrielle digitale enkelt- og flersløyfe PID-kontrollere.)

Styresignalbegrensning . Det er to forutsetninger for å begrense styresignalet:

1) amplituden til utgangssignalet kan ikke overskride rekkevidden til DAC-en ved utgangen til datamaskinen;

2) driftsområdet til MI er også alltid begrenset. Ventilen åpner ikke mer enn 100 %; motoren kan ikke forsynes med ubegrenset strøm og spenning.

Derfor må kontrollalgoritmen inkludere en funksjon som begrenser utgangssignalet. I noen tilfeller må et dødbånd, eller dødbånd, defineres.

Hvis en kontroller med en inkrementell algoritme brukes, kan endringene i kontrollsignalet være så små at MI ikke kan behandle dem. Hvis kontrollsignalet er tilstrekkelig til å påvirke MI, er det tilrådelig å unngå små, men hyppige operasjoner, som kan akselerere slitasjen.

En enkel løsning er å summere små endringer i styrevariabelen og gi et styresignal MI først etter at en terskelverdi er overskredet. Innføringen av en dødsone gir mening bare hvis den overskrider oppløsningen til DAC-en ved utgangen til datamaskinen

Forebygging av integrert metning. Integrert avvikling oppstår når en PI- eller PID-regulator må kompensere for en feil som er utenfor rekkevidden til den kontrollerte variabelen i lang tid. Siden utgangen til regulatoren er begrenset, er feilen vanskelig å oppheve.

Hvis kontrollfeilen forblir tegnet i lang tid, blir verdien av integreringskomponenten til PID-regulatoren veldig stor. Dette skjer hvis styresignalet er begrenset så mye at den beregnede utgangen til regulatoren avviker fra den virkelige utgangen til MI.

Siden integraldelen først blir null en tid etter at feilverdien har endret fortegn, kan integralmetning føre til store overskudd. Integrert metning er resultatet av ikke-lineariteter i systemet assosiert med klipping av utgangskontrollsignalet og kan aldri observeres i et lineært system.

Påvirkningen av den integrerte delen kan begrenses av betinget integrasjon. Så lenge feilen er stor nok, er dens integrerte del nødvendig for å danne styresignalet, men den proporsjonale delen er tilstrekkelig for kontroll.

Den integrerte delen som brukes til å eliminere stasjonære feil er bare nødvendig i tilfeller der feilen er relativt liten. Med betinget integrasjon tas denne komponenten i betraktning i sluttsignalet bare hvis feilen ikke overskrider en viss terskelverdi. Ved store feil fungerer PI-kontrolleren som en P-kontroller. Å velge en terskelverdi for å aktivere integralleddet er ikke en lett oppgave. I analoge kontrollere utføres betinget integrasjon ved hjelp av en Zener-diode (begrenser), som er koblet parallelt med en kondensator i tilbakemeldingskretsen til operasjonsforsterkeren i integreringsblokken til kontrolleren. Et slikt opplegg begrenser bidraget til det integrerte signalet.

I digitale PID-kontrollere er integrert metning lettere å unngå. Den integrerte delen justeres ved hvert samplingsintervall slik at kontrollerens utgang ikke overskrider en viss grense.

Kontrollsignalet beregnes først ved hjelp av en PI-kontrolleralgoritme og sjekkes deretter for å se om det overskrider de angitte grensene:

u = u min , hvis u d < u min ;

u = u d , hvis u min ≤ u d < u maks ;

u = u maks , hvis u d ≤ u maks ;

Etter å ha begrenset utgangssignalet, tilbakestilles den integrerte delen av regulatoren. Nedenfor er et eksempelprogram for en PI-kontroller med metningsbeskyttelse.

Så lenge styresignalet holder seg innenfor de fastsatte grensene, påvirker ikke den siste setningen i programteksten den integrerte delen av kontrolleren.

(*initialisering*) c1:=K*taus/Ti;

(*regulator*)

Ipart:= Ipart + c1*e;

ud:=K*e+Ipart; (*kontrollsignalberegning*)

hvis (ud

annet hvis (ud< umax) then u:= ud

Ipart:=u-K*e; (* "anti-metning" integrert delkorreksjon *)

En illustrasjon av problemet med integrert metning for en posisjoneringsdrivenhet med en PI-kontroller er videre i fig. 30.4.

Jevn veksling av driftsmoduser. Når du bytter fra manuell til automatisk modus, kan kontrollutgangen hoppe selv om kontrollfeilen er null. Årsaken er at integralleddet i kontrolleralgoritmen ikke alltid er lik null. Kontrolleren er et dynamisk system, og den integrerte delen er et av elementene i den interne tilstanden, som må være kjent når du endrer kontrollmodus.

Hoppet i utgangsverdien til kontrolleren kan forhindres, og modusendringen i dette tilfellet kalles en støtløs overgang (støtløs overføring).

To situasjoner er mulige: a) overgang fra manuell til automatisk modus eller omvendt; b) endre regulatorens parametere.

En jevn overgang i tilfelle a) for en analog kontroller oppnås ved å bringe prosessen manuelt til en tilstand der den målte utgangsverdien er lik referanseverdien.

Prosessen opprettholdes i denne tilstanden så lenge kontrollerutgangen er null. I dette tilfellet er den integrerte delen også null, og siden feilen er null, oppnås en jevn overgang. Denne prosedyren er også gyldig for digitale kontrollere.

En annen metode er å sakte bringe referanseverdien til den nødvendige sluttverdien.

Først settes referanseverdien lik gjeldende måling, og justeres deretter gradvis manuelt til ønsket verdi.

Hvis denne prosedyren utføres sakte nok, forblir den integrerte delen av kontrollsignalet så liten at en jevn overgang sikres. Ulempen med denne metoden er at den krever ganske lang tid, noe som avhenger av prosessens art.

Begrenser endringshastigheten til styresignalet . I mange kontrollsystemer er det nødvendig å begrense både amplituden og endringshastigheten til styresignalet. For dette brukes spesielle beskyttelseskretser, koblet etter kanalen for manuelt å legge inn referanseverdien. u c (t) og overføre det filtrerte signalet til kontrolleren u L (t), som vist i fig. 30.5.

Som et resultat "ser" prosessen dette kontrollsignalet i stedet for det manuelt angitte. Denne metoden brukes vanligvis i reguleringen av elektriske stasjoner. Begrensning av endringshastigheten til signalet kan oppnås med en enkel tilbakemeldingssløyfe.

Håndkontrollsignal u c (t), som fungerer som en referanse, sammenlignes med et gyldig styresignal u L (t). For det første er forskjellen deres begrenset av grensene uemin og uemÅh.

Den resulterende verdien blir deretter integrert, med integralet tilnærmet med en endelig sum.

Algoritmen for å begrense endringshastigheten er som følger:

hvis (ue< uemin) then uelim:= uemin (*функция ограничения*) else if (ue < uemax) then uelim:= ue

annet uelim:= uemax;

uL = uL_gammel + taus*uelim;

Beregningsfunksjoner til PID-kontrolleralgoritmen. Den digitale implementeringen av PID-kontrolleren, på grunn av den sekvensielle karakteren til beregningene, fører til forsinkelser som ikke finnes i analog teknologi. I tillegg krever noen begrensninger (metningsbeskyttelse og myke overgangsalgoritmer) at regulatorutgangen og MI-pickupen skjer samtidig. Derfor må beregningsforsinkelser holdes på et minimum. For å gjøre dette, beregnes noen elementer i den digitale regulatoren før prøvetakingstiden.

For en regulator med metningsbeskyttelse kan den integrerte delen beregnes på forhånd ved å bruke foroverforskjeller

u Jeg (k + 1) =u Jeg (k)+c 1 · e (k) + c 2 · [u (k) – u d (k) ] ,

hvor u – begrenset verdi u d ;

T t er en koeffisient som kalles sporingstidskonstanten.

Differensialdelen ser ut som

c 3 = (1– b) · K· T d /t s ;

x (k- 1) = b· u D (k- 1)+c 3 · y (k- 1).

variabel x kan oppdateres umiddelbart etter tidspunktet k

x (k) = b· x(k- 1)+c 3 (1 – b) · y (k).

På denne måten, u D (k + 1) kan beregnes fra (24.2) så snart måleresultatet er oppnådd y(k + 1).

Optimalisering av beregningene er nødvendig, siden den digitale regulatoren noen ganger må utføre flere tusen kontrolloperasjoner per sekund. Under disse forholdene er det viktig at noen koeffisienter er tilgjengelig umiddelbart, i stedet for å beregnes på nytt hver gang. I tillegg har ikke industrielle regulatorer de raskeste prosessorene ( Jeg 386, 486). Derfor påvirker rekkefølgen og typen av beregninger i stor grad hastigheten på kontrolloperasjoner.

PID-algoritme . Et eksempel på et PID-kontrollerprogram i Pascal. Beregning av koeffisienter c 1 ,c 2 og c 3 må bare gjøres hvis regulatorens parametere endres K, T Jeg , T d og T f. Kontrolleralgoritmen kjøres på tidspunktet for hver prøve. Programmet har beskyttelse mot metning av den integrerte komponenten.

(*Forberegning av koeffisienter*)

c1:=K*taus / Ti; (* Ligning 23,7 *)

с2:= taus / Tt; (* ligning 24.1 *)

beta:=Td / (Td+taus*N); (* ligning 24.1 *)

c3:= K*Td*(l-beta) / taus; (* ligning 24.2 *)

c4:= c3*(1 - beta); (* lokal konstant*)

(* Kontrollalgoritme *)

uc:=ADinput(ch1); (* referanseverdiinngang, analog inngang *)

y:= AD_input(ch2); (* måleinngang, analog inngang *)

e:= uc-y; (* kontrollfeilberegning *)

ppart:= K*e; (*proporsjonal del*)

dpart:= x - (c3*y); (* differensialdel, *)

ud:=uO+ppart+ipart+dpart; (* regulatorutgang før klipping*)if(ud

Send ditt gode arbeid i kunnskapsbasen er enkelt. Bruk skjemaet nedenfor

Studenter, hovedfagsstudenter, unge forskere som bruker kunnskapsbasen i studiene og arbeidet vil være deg veldig takknemlig.

Vert på http://www.allbest.ru

Utdannings- og vitenskapsdepartementet i Den russiske føderasjonen

Federal State Budgetary Education Institution

høyere profesjonsutdanning

"KUBAN STATE UNIVERSITY"

(FGBOU VPO "KubGU")

BACHELORS AVSLUTTENDE KVALIFIKASJONSARBEID

Utvikling og design av PID-kontrollere

Arbeidet ble utført av Roman Valerievich Presnyakov

veileder

dr. Fysisk.-Matte. vitenskap, professor

E.N. Tumaev

Kontrollør

cand. Fysisk.-Matte. Sciences, førsteamanuensis A. A. Martynov

Krasnodar 2015

Avsluttende kvalifiserende arbeid 83 sider, 29 bilder, 42 kilder.

PID-KONTROLL, EMBEDDED SYSTEMS, MICROCONTROLLERS, SOFTWARE MODULES, MSP430, INTERRUPT

Studieobjektet for det endelige kvalifiseringsarbeidet er studiet av de generelle prinsippene for å bygge proporsjonale-integral-differensielle teknologiske kontrollere og designe en algoritme for temperaturkontrollere basert på billige MSP430 mikrokontrollere (Texas Instruments). Oppgaven gir en oversikt over midlene til moderne mikrokontrollere og prinsippene for deres drift.

Analysen av problemene med maskinvare- og programvareimplementering av teknologiske mikroprosessorkontrollere utføres. Det gis anbefalinger for design av mikroprosessorbaserte måle- og kontrollinstrumenter og oppretting av programvare for innebygde systemer. En variant av implementeringen av PID-kontrolleralgoritmen er foreslått. Et særtrekk er bruken av algoritmer som utelukker bruken av flyttall.

Betegnelser og forkortelser

Introduksjon

2. Følsomhetsfunksjoner. Digital Pid-ligning

2.2 Diskret utforming av kontrolleren. Digital PID-ligning

3. Regulatorisk kvalitet

3.1 Svekkelse av påvirkning av ytre forstyrrelser. Kvalitetskriterier

4. Stille inn kontrollerparametere. grunnleggende prinsipper

4.1 Valg av regulatorparametere. Manuelle og automatiske innstillinger

5. Programmering av innebygde systemer

5.1 Generelle prinsipper for utvikling av innebygde systemer

5.2 Stadier for å lage programvare for innebygde systemer

5.3 Hierarki av kjørbar kode i innebygde systemer

6. Algoritme for den opprettede programvaren

6.1 Beskrivelse av operasjonsalgoritmen til PID-temperaturkontrolleren basert på MSP430F149 mikrokontrolleren

Konklusjon

Liste over kilder som er brukt

Betegnelser og forkortelser

temperaturkontroll mikrokontroller

	mikrokontroller
PID-algoritme	Proporsjonal-integral-differensial-algoritme
	maskinvareabstraksjonslag (maskinvareabstraksjonslag)
	Integrert utviklingsmiljø (integrert utviklingsmiljø)
	pulsbreddemodulasjon
	programmerbar logisk kontroller
	tilsynskontroll og datainnsamling (tilsynskontroll og datainnsamling)
	serielt perifert grensesnitt (serielt perifert grensesnitt)
	appli(applikasjonsprogrammeringsgrensesnitt)
	automatisert arbeidsplass
	programvare

INTRODUKSJON

Kontrollen av teknologiske prosesser ved hjelp av kontrollere som opererer i henhold til proporsjonal-integral-differensialloven (PID-kontrollere) gjør det mulig å opprettholde den nødvendige teknologiske verdien med tilstrekkelig høy nøyaktighet og akseptabel støyimmunitet mot eksterne forstyrrende påvirkninger. Moderne PID-kontrollere er implementert både som en programvaremodul til et SCADA-system som kjøres på en automatisert arbeidsstasjon (AWS) eller en programmerbar logisk kontroller (PLC), og som separate prosesskontrollere plassert på lokale og sentrale styreskap. Som de grunnleggende elementene i informasjonsbehandling og kontroll, brukes ofte mikroprosessorer med begrenset funksjonalitet, noe som reiser problemet med mangel på maskinvareressurser og en økning i kostnadene til systemet.

Formålet med dette arbeidet er å gjennomgå prinsippene for å bygge proporsjonal-integral-deriverte regulatorer og å utvikle, på bakgrunn av gjennomgangen, prinsippene for å lage en temperatur PID-regulator.

Ved opprettelse av en temperatur PID-kontroller ble det brukt en programmerbar mikroprosessor teknologisk målerregulator F0303.2 basert på MSP430F149 mikrokontroller, MSP-FET430UIF programmerer, P3003 spenningskomparator med et spenningsutgangsområde fra 10 nV til 11.111110 V og en nøyaktighetsklasse på 50. . Mikrokontrollerprogrammet ble opprettet i det integrerte utviklingsmiljøet IAR Embedded Workbench for MSP430 6. Den tekniske dokumentasjonen ble hentet fra nettsiden til mikrokontrollerprodusenten.

For full implementering av PID-kontroll i en mikroprosessorenhet, er det nødvendig å implementere følgende undersystemer:

Måling delsystem

PID-algoritmebehandlingsundersystem

Management User Interface Subsystem

Regulatorisk påvirkningsutgang undersystem

1. Prinsipper for å lage PID-kontrollere

1.1 Generelle spørsmål om implementering av PID-kontrollere

For praktisk implementering er det nødvendig å ta hensyn til funksjonene generert av de virkelige betingelsene for applikasjon og teknisk implementering. Disse funksjonene inkluderer:

Finitt dynamisk område av endringer i fysiske variabler i systemet (f.eks. begrenset varmeeffekt, begrenset ventilkapasitet);

Det er ikke alltid mulig å endre tegnet på kontrollhandlingen (for eksempel er det ofte ikke noe kjøleskap i temperaturvedlikeholdssystemet, motoren har kanskje ikke et reversslag, ikke alle fly har et negativt skyvesystem);

Begrenset målenøyaktighet, som krever spesielle tiltak for å utføre differensieringsoperasjonen med en akseptabel feil;

Tilstedeværelsen av typiske ikke-lineariteter i nesten alle systemer: metning (begrenser det dynamiske området for variable endringer), begrenser svinghastigheten, hysterese og tilbakeslag;

Teknologisk spredning og tilfeldige variasjoner av parametrene til kontrolleren og objektet;

Diskret implementering av kontrolleren;

Behovet for jevn (støtfri) veksling av kontrollmoduser;

1.2 PID-derivatmontering

Problemet med numerisk differensiering er ganske gammelt og vanlig i både digitale og analoge kontrollere. Dens essens ligger i det faktum at den deriverte vanligvis beregnes som forskjellen mellom to variabler av nær størrelse, så den relative feilen til den deriverte viser seg alltid å være større enn den relative feilen til den numeriske representasjonen av den differensierbare variabelen.

Spesielt hvis inngangen til differensiatoren mottar et sinusformet signal A * sin (sht), får vi ved utgangen A * w * cos (sht), det vil si med økende frekvens w, amplituden til signalet ved utgangen til differensiatoren øker. Differensiatoren forsterker med andre ord høyfrekvent interferens, korte serier og støy.

Hvis interferensen forsterket av differensiatoren ligger utenfor driftsfrekvensområdet til PID-kontrolleren, kan de dempes ved hjelp av et høypassfilter. Den strukturelle implementeringen av en differensiator med filter er vist i figur 1. Her

det vil si at overføringsfunksjonen til den resulterende differensiatoren D(s) kan representeres som produktet av overføringsfunksjonen til en ideell differensiator og overføringsfunksjonen til et førsteordens filter:

hvor koeffisienten N setter grensefrekvensen til filteret og vanligvis velges lik 2…20;

T/N -- filtertidskonstant;

s er den komplekse frekvensen.

Større høyfrekvent støydemping kan oppnås med et separat filter som kobles i serie med PID-regulatoren. Vanligvis brukes et andreordens filter med overføringsfunksjon

Filtertidskonstanten velges lik TF = Ti/N, hvor N = 2…20, Ti er integrasjonskonstanten til PID-regulatoren. Det er tilrådelig å ikke velge grensefrekvensen til filteret under frekvensen 1/Ti, siden dette kompliserer beregningen av regulatorparametrene og stabilitetsmarginen.

Figur 1 - Strukturell implementering av differensialleddet til PID-kontrolleren

I tillegg til differensieringsstøy, påvirkes ytelsen til PID-regulatoren av målestøy. Gjennom tilbakemeldingssløyfen kommer disse lydene inn i systeminngangen og vises deretter som spredningen av kontrollvariabelen u. Høyfrekvent støy er skadelig fordi det forårsaker akselerert slitasje på rørledninger og elektriske motorer.

Fordi kontrollobjektet vanligvis er et lavpassfilter, går målestøy sjelden gjennom kontrollsløyfen til systemutgangen. Imidlertid øker de målefeilen y(t) og reduserer reguleringsnøyaktigheten.

I PID-kontrollere, støy med et spektrum i lavfrekvensområdet, forårsaket av ytre påvirkninger på kontrollobjektet, og høyfrekvent støy forbundet med elektromagnetisk interferens, støy på strøm- og jordbussen, med sampling av det målte signalet, og andre årsaker skilles ut. Lavfrekvent støy er modellert som en ekstern forstyrrelse d(s), høyfrekvent støy er modellert som målestøy n(s).

1.3 Integrert node av PID-kontrolleren. integrert metning

Ved stabil drift og med små forstyrrelser er de fleste systemer med PID-regulatorer lineære. Imidlertid krever prosessen med å gå inn i regimet nesten alltid å ta hensyn til ikke-lineariteten til typen "begrensning". Denne ikke-lineariteten skyldes naturlige begrensninger på effekt, hastighet, rpm, rotasjonsvinkel, ventiltverrsnittsareal, dynamisk område, etc. Kontrollsløyfen i et system som er i metning (når variabelen har nådd grensen) viser seg å være åpen, siden når variabelen ved inngangen til koblingen med grensen endres, forblir dens utgangsvariabel uendret.

Den mest typiske manifestasjonen av begrensningsmodusen er den såkalte "integrerte metningen", som oppstår når systemet når modusen i kontrollere med en integrasjonskonstant Ti? 0. Integrert metning fører til en forsinkelse i transientprosessen (figur 2 og 3). En lignende effekt oppstår på grunn av begrensningen av proporsjonal og integrert ledd for PID-kontrolleren (figur 4 og 5). Imidlertid blir integrert metning ofte forstått som et sett med effekter assosiert med en ikke-linearitet av typen "begrensning".

Ti = 0,1 s; T2 = 0,05 s; L = 0,02 s; K = 2; Ti = 0,06 s; Td = 0

Figur 2 - Responsen til utgangsvariabelen y(t) på hoppet i inngangshandlingen r(t) for PI-kontrolleren under betingelsen om å begrense effekten ved inngangen til objektet u(t) og uten begrensning (andre bestille objekt)

T1 = 0,1 s; T2 = 0,05 s; L = 0,02 s; K = 2; Ti = 0,06 s; Td = 0

Figur 3 - Signal ved inngangen til objektet u(t) med og uten effektbegrensning (andre ordens objekt)

K = 10; Ti = 0,014 s; Td = 0,3 s; T1 = 0,1 s; T2 = 0,05 s; L = 0,02 s

Figur 4 - Responsen til utgangsvariabelen y(t) på hoppet i inngangshandlingen r(t) for PID-kontrolleren under betingelsen om å begrense effekten ved inngangen til objektet u(t) og uten begrensning (andre bestille objekt)

T1 = 0,1 s; T2 = 0,05 s; L = 0,02 s; K = 10; Ti = 0,014 s; Td = 0,3 s

Figur 5 - Signalet ved inngangen til objektet u(t) i sløyfen med PID-kontrolleren under betingelse av effektbegrensning og uten (andre ordens objekt)

og andre orden

hvor Kp er overføringskoeffisienten i stabil tilstand;

T, T1, T2 - tidskonstanter;

L - transportforsinkelse.

Essensen av problemet med integralmetning er at hvis signalet ved inngangen til kontrollobjektet u(t) har gått inn i metnings(begrensnings)sonen, og mistilpasningssignalet r(t) - y(t) ikke er lik med null, integratoren fortsetter å integrere, det vil si at signalet øker ved utgangen, men dette signalet deltar ikke i reguleringsprosessen og påvirker ikke objektet på grunn av metningseffekten. Kontrollsystemet blir i dette tilfellet ekvivalent med et åpent system, hvis inngangssignal er lik metningsnivået til styresignalet u(t).

For termiske systemer er den nedre grensen vanligvis null varmeeffekt, mens PID-kontrolleren krever at en "negativ varmeeffekt" påføres objektet, det vil si kjøling av objektet. Effekten av integrert metning har vært kjent i lang tid. I analoge regulatorer var elimineringen ganske vanskelig, siden problemet ikke kunne løses algoritmisk, men bare ble løst av maskinvare.

Med bruk av mikroprosessorer kan problemet løses mye mer effektivt. Metoder for å eliminere integrert metning er vanligvis gjenstand for oppfinnelser, tilhører forretningshemmeligheten til produksjonsbedrifter og er beskyttet av patenter.

Begrenser slew rate for inndatahandlingen. Siden den maksimale verdien av inngangshandlingen på kontrollobjektet u(t) avtar med en reduksjon i differansen r(t) - y(t), for å eliminere begrensningseffekten, kan du ganske enkelt redusere slew rate for settpunktsignalet r(t), for eksempel ved å bruke et filter. Ulempen med denne metoden er reduksjonen i systemhastighet, samt manglende evne til å eliminere den integrerte metningen forårsaket av eksterne forstyrrelser, og ikke av settpunktsignalet.

Når kontrollhandlingen på objektet når metning, bryter tilbakemeldingen og den integrerte komponenten fortsetter å vokse, selv om den skulle ha falt i fravær av metning. Derfor er en av metodene for å eliminere den integrerte metningen at kontrolleren overvåker størrelsen på kontrollhandlingen på objektet, og så snart den når metning, går kontrolleren inn i et programvareforbud for integrasjon for den integrerte komponenten.

Metningskompensasjon med ekstra tilbakemelding. Effekten av integrert metning kan svekkes ved å overvåke tilstanden til aktuatoren som går inn i metning og kompensere signalet som tilføres inngangen til integratoren. Strukturen til et system med en slik kompensator er vist i figur 6.

Figur 6 - Kompensasjon for effekten av integralmetning ved hjelp av ekstra tilbakemelding for overføring av feilsignalet es til inngangen til integratoren

Prinsippet for arbeidet er som følger. Systemet genererer et misforholdssignal mellom inngangen og utgangen til aktuatoren es = u - v. Signalet ved utgangen til aktuatoren måles eller beregnes ved hjelp av en matematisk modell (Figur 6). Hvis es = 0, tilsvarer dette ingen kompensator og vi får en normal PID-regulator. Hvis utøvende enhet metter, deretter v > u og es< 0. При этом сигнал на входе интегратора уменьшается на величину ошибки es, что приводит к замедлению роста сигнала на выходе интегратора, уменьшению сигнала рассогласования и величины выброса на переходной характеристике системы (рисунки 7 и 8). Постоянная времени Ts определяет степень компенсации сигнала рассогласования.

Figur 7 - Systemrespons på et enkelt hopp r(t) for forskjellige verdier av tidskonstanten Ts

K = 7; Ti = 0,01 s; Td = 0,1 s, T1 = 0,1 s; T2 = 0,05 s; L = 0,01 s

Figur 8 - Systemrespons på feilsignalet es (andreordens objekt, kontrollerparametere:

I noen kontrollere er inngangen u til sammenligningsenheten es skilt ut som en separat inngang - "sporingsinngangen", noe som er praktisk når du bygger komplekse kontrollsystemer og når du kaster flere kontrollere.

Betinget integrasjon. Denne metoden er en generalisering av det algoritmiske forbudet mot integrasjon. Etter utbruddet av forbudet forblir integreringskomponenten konstant, på samme nivå som den hadde i det øyeblikket integreringsforbudet dukket opp. Generaliseringen er at forbudet mot integrering skjer ikke bare når metning er nådd, men også under visse andre forhold.

En slik betingelse kan for eksempel være oppnåelse av feilsignalet e eller utgangsvariabelen y av en viss spesifisert verdi. Når du slår av integrasjonsprosessen, er det nødvendig å overvåke tilstanden til integratoren i det øyeblikket den slås av. Hvis det akkumuleres en feil og metningsgraden øker, blir integrasjonen slått av. Hvis metningsgraden synker i det øyeblikket den slås av, forblir integratoren på.

Figur 9 viser et eksempel på en transient prosess i et system med integratoren slått av når utgangsverdien y(t) når en gitt verdi (y = 0, y = 0,2, y = 0,8).

Figur 9 - Respons på et enkelt hopp r(t) av et system med aktuatormetning ved forskjellige integratoravstengningsnivåer y

Begrenset integrator. I en variant av implementeringen av PI-kontrolleren ble det presentert en integrator i tilbakemeldingssløyfen. Hvis denne kretsen er supplert med en limiter (Figur 10), vil signalet u ved utgangen aldri gå utover grensene satt av limiter-terskelverdiene, noe som reduserer oversvinget i systemets transiente respons (Figur 12). Figur 11 viser en modifikasjon av en slik begrenser.

Modellen av klippeeffekten kan forbedres hvis, etter å ha overskredet nivået der klippingen skjer, reduseres signalet ved utgangen til modellen (Figur 13). Dette akselererer gjenopprettingen av systemet fra metningsmodus.

Figur 10 - Modifikasjon av integratoren med begrenser (parallell)

Figur 11 - Modifikasjon av integratoren med en begrenser (i serie)

Figur 12 - Respons på et enkelt hopp r(t) av et system som inneholder

integrator med øvre begrensning Uup

Figur 13 - Forbedret overføringsfunksjon av klippeeffektmodell

1.4 Stabilitetsmargin for systemet. Nyquist-kriterium

Muligheten for tap av stabilitet er den største ulempen med tilbakemeldingssystemer. Derfor er å sikre den nødvendige stabilitetsmarginen det viktigste trinnet i utviklingen og innstillingen av PID-kontrolleren.

Stabiliteten til et system med en PID-kontroller er systemets evne til å gå tilbake til å spore settpunktet etter opphør av ytre påvirkninger. I sammenheng med denne definisjonen betyr ytre påvirkninger ikke bare ytre forstyrrelser som virker på objektet, men alle forstyrrelser som virker på noen del av det lukkede systemet, inkludert målestøy, tidsmessig settpunkt-ustabilitet, prøvetakings- og kvantiseringsstøy, støy og beregningsfeil. Alle disse forstyrrelsene forårsaker avvik i systemet fra likevektsposisjonen. Hvis

etter at deres innflytelse er avsluttet, går systemet tilbake til likevektsposisjonen, da anses det som stabilt. Ved analyse av stabiliteten til PID-regulatorer er det vanligvis begrenset til å studere systemets respons på en trinnvis endring i settpunktet r(t), målestøy n(t) og eksterne forstyrrelser d(t). Tapet av stabilitet manifesterer seg som en ubegrenset økning i den kontrollerte variabelen til objektet eller som dets oscillasjon med økende amplitude.

Under produksjonsforhold fører forsøk på å oppnå stabiliteten til et system med en PID-kontroller empirisk, uten identifisering, ikke alltid til suksess (for det første gjelder dette systemer med et eller flere objekter av høy orden som er vanskelige å identifisere , samt systemer med stor transportforsinkelse). Det ser ut til at stabilitet er en mystisk egenskap som ikke alltid kan kontrolleres. Men hvis prosessen identifiseres nøyaktig nok, forsvinner mystikken og stabilitetsanalysen reduseres til analysen av en differensialligning som beskriver en lukket sløyfe med tilbakemelding. Av praktisk interesse er analysen av stabilitetsmarginen, det vil si bestemmelsen av de numeriske verdiene til kriteriene som lar deg indikere hvor langt systemet er fra ustabiliteten.

Den mest komplette informasjonen om stabilitetsmarginen til systemet kan fås ved å løse en differensialligning som beskriver et lukket system under ytre forstyrrelser. Imidlertid er denne prosessen for tidkrevende, derfor brukes forenklede metoder for lineære systemer for å estimere stabilitetsmarginen uten å løse ligninger. Vi vil vurdere to estimeringsmetoder: bruk av hodografen til den komplekse åpne sløyfefrekvensresponsen (Nyquist-kriteriet) og bruk av logaritmisk frekvensrespons og faserespons (Bode-plott).

Et stabilt system kan bli ustabilt med små endringer i parameterne, for eksempel på grunn av deres teknologiske spredning. Derfor vil vi videre analysere følsomhetsfunksjonen til et system med en PID-kontroller, som lar oss identifisere forholdene under hvilke systemet blir grovt (ufølsomt for endringer i parameterne). Et system som opprettholder en gitt stabilitetsmargin over hele spekteret av parameterendringer på grunn av deres teknologiske variasjon, aldring, driftsforhold, over hele spekteret av lastparameterendringer, så vel som over hele spekteret av forstyrrelser som virker på systemet i virkeligheten driftsforhold, kalles robuste. Noen ganger brukes robusthet og frekkhet som likeverdige begreper.

Nyquist-kriterium. Tenk på et system som består av en kontroller R og et kontrollobjekt P (Figur 14), som oppnås ved å eliminere settpunktsignalkretsen fra et klassisk system med en PID-kontroller. Vi vil anta at tilbakemeldingen er åpen, og for å lukke den er det nok å koble sammen punktene x og y. La oss nå anta at inngangen x får et signal

Deretter, etter å ha gått gjennom kontrolleren og kontrollobjektet, vil dette signalet vises på utgangen y med en endret amplitude og fase i formen:

y(t) = ? |G(jw0)|sin(w0t + ?), (4)

hvor G(jsh) = R(jsh)P(jsh) er den komplekse frekvensresponsen (CFC) til systemet, ? = arg(G(jш0)) - CCH-argument, |G(jш0)| - CFC-modul ved frekvens w0. Således, når du passerer gjennom regulatoren og objektet, vil signalamplituden endres proporsjonalt med modulen, og fasen - med verdien av CFC-argumentet.

Figur 14 - Struktur av et åpent sløyfe-kontrollsystem med en PID-kontroller for stabilitetsanalyse

Hvis vi nå lukker punktene x og y, så vil signalet sirkulere i en lukket sløyfe, og betingelsen y(t) = x(t) vil være oppfylt. Hvis i tillegg |G(jш0)| ? 1 og? \u003d 180 °, det vil si etter å ha passert gjennom sløyfen, kommer signalet inn i kontrollerinngangen i samme fase som i forrige syklus, og etter hver passasje gjennom sløyfen vil amplituden til det sinusformede signalet øke til det når grensen til systemets linearitetsområde, hvoretter oscillasjonsformen blir forskjellig fra sinusformet. I dette tilfellet kan den harmoniske lineariseringsmetoden brukes til å analysere stabiliteten, når bare den første harmoniske av det forvrengte signalet vurderes. I stabil tilstand, etter at oscillasjonsamplituden er begrenset, på grunn av likheten y(t) = x(t), vil følgende betingelse være oppfylt:

|G(jw0)|=1, dvs. G(jw0)= - 1 (5)

Ved å løse likningen G(jw0) = -1, kan du finne frekvensen av svingninger w0 i et lukket system.

Den komplekse frekvensresponsen G(jш) er grafisk avbildet i form av en hodograf (Nyquist-diagram) - en graf i koordinatene Re og Im (Figur 15). Pilen på hodograflinjen indikerer bevegelsesretningen til "blyanten" med økende frekvens. Punktet G(jw0) = -1, som tilsvarer betingelsen for eksistensen av udempede oscillasjoner i systemet, har på denne grafen koordinatene Re = -1 og Im = 0. Derfor er Nyquists stabilitetskriterie formulert som følger : en krets som er stabil i åpen tilstand vil forbli stabil og etter lukking, hvis CFC i åpen tilstand ikke dekker punktet med koordinater [-1, j0]. Mer strengt, når du beveger deg langs hodografbanen i retning av økende frekvens, må punktet [-1, j0] forbli til venstre slik at den lukkede sløyfen er stabil.

K=6; T1 = T2 = 0,1 s; L = 0,01 s

Figur 15 - Tre hodografer av CFC til et åpent system G(jw) for et andreordens objekt

Figur 16 viser responsene til et lukket system med tre forskjellige hodografer (Figur 15) på et enkelt settpunkttrinn. I alle tre tilfellene er systemet stabilt, men dempingshastigheten for svingninger og formen på overgangen

prosessen deres er annerledes. Det er intuitivt klart at et system med parametere Ti = 0,01 s, Td = 0,1 s er nærmest å gå inn i en tilstand av udempede oscillasjoner med en liten endring i parameterne. derfor

når du designer en PID-kontroller, er det viktig å sikre ikke så mye stabilitet som dens reserve, som er nødvendig for normal funksjon av systemet under reelle forhold.

Stabilitetsmarginen er estimert som graden av avstand til CFC fra det kritiske punktet [-1, j0]. Hvis |G(jш0)|< 1, то можно найти, во сколько раз осталось увеличить передаточную функцию, чтобы результирующее усиление вывело систему в колебательный режим: gm|G(jщ0)| = 1, откуда

Forsterkningsmarginen gm er verdien som overføringsfunksjonen til et åpent sløyfesystem G(jsh180) må multipliseres med slik at modulen ved en faseforskyvningsfrekvens på 180 ° (sh180) blir lik 1. Hvis ved en frekvens på w180 den åpne sløyfeforsterkningen er G(jsh180) = -1/gm (fig. 15), så vil en ekstra forsterkning på gm bringe systemet til punktet [-1, j0], siden (-1/gm) gm = -1. Konseptet med fasemargin introduseres på samme måte: dette er minimumsverdien m som det er nødvendig å øke faseforskyvningen med i et åpent system arg(G(jw)) slik at den totale faseforskyvningen når 180°, dvs.

"+"-tegnet før arg(G(jш1)) er fordi arg(G(jш1))< 0. Для оценки запаса устойчивости используют также минимальное расстояние sm от кривой годографа до точки [-1, j0] (рисунок 15).

I praksis anses verdiene gm = 2...5,m = 30...60°, sm = 0,5...0,8 som akseptable. For grafen i figur 15 har disse kriteriene følgende verdier:

Gml = 12,1; ml = 15°; sm1 = 0,303 (for tilfellet Ti = 0,01 s,

Gm2 = 11,8; m2 = 47,6°; sm2 = 0,663 (for tilfellet Ti = 0,05 s,

Gm3 = 1,5; m3 = 35,2°; sm3 = 0,251 (for tilfellet Ti = 0,05 s,

Hvis hodografkurven skjærer den reelle aksen på flere punkter, så for å vurdere stabilitetsmarginen, ta den som er nærmest punktet [-1, j0]. Med en mer kompleks hodograf kan et estimat av stabilitetsmarginen som en forsinkelsesmargin brukes. Forsinkelsesmarginen er minimumsforsinkelsen som legges til løkken for å gjøre den ustabil. Oftest brukes dette kriteriet til å vurdere stabilitetsmarginen til systemer med Smith-prediktoren.

Frekvensstabilitetskriterium.For en grafisk representasjon av overføringsfunksjonen til et åpent system og en vurdering av stabilitetsmarginen kan logaritmisk frekvensrespons og faserespons brukes (Figur 17). For å vurdere fasemarginen, først, ved å bruke frekvensresponsen, blir frekvensen u1 (grensefrekvens, eller enhetsforsterkningsfrekvens) funnet, ved hvilken G(ju1) = 1, deretter blir den tilsvarende fasemarginen funnet fra PFC. For å estimere forsterkningsmarginen, ved å bruke PFC, finn først frekvensen w180, hvor faseforskyvningen er 180 °, og finn deretter forsterkningsmarginen fra frekvensresponsen. Figur 17 viser eksempler på grafiske konstruksjoner for å estimere forsterkningen og fasemarginen for systemet, hvor hodografene er vist i figur 15.

Hvis fasemarginen for åpen sløyfe er 0° eller forsterkningsmarginen er 1, vil systemet være ustabilt etter at tilbakemeldingssløyfen er lukket.

Figur 16 - Transient respons av et lukket system, som

har hodografer vist i figur 15

2. Følsomhetsfunksjoner. digital PID-kontrollerligning

2.1 Følsomhetsfunksjoner. robusthet. Støtfri veksling av kontrollmoduser

Overføringsfunksjonen til et virkelig objekt P(er) kan endres under drift med verdien DP(er), for eksempel på grunn av endringer i belastningen på motorakselen, antall egg i inkubatoren, nivået eller sammensetningen av væsken i autoklaven, på grunn av aldring og slitasje på materialet, utseende av tilbakeslag, smøreendringer osv. Et riktig utformet automatisk kontrollsystem bør opprettholde kvalitetsindikatorene ikke bare under ideelle forhold, men også i nærvær av de oppførte skadelige faktorene. For å vurdere påvirkningen av en relativ endring i overføringsfunksjonen til objektet DP / P på overføringsfunksjonen til det lukkede systemet Gcl

y(s) = r(s), Gcl(s) = (8)

finn differensialen dGcl:

Ved å dele begge sider av denne likheten med Gcl og erstatte Gcl = PR/(1+PR) på høyre side, får vi:

Figur 17 - Evaluering av forsterkningen og fasemarginen for et system med en hodograf vist i figur 15

Fra (10) er betydningen av koeffisienten S synlig - den karakteriserer graden av påvirkning av den relative endringen i overføringsfunksjonen til objektet på den relative endringen i overføringsfunksjonen til den lukkede sløyfen, det vil si at S er koeffisienten av følsomheten til den lukkede sløyfen for variasjonen i objektets overføringsfunksjon. Siden koeffisienten S \u003d S (jsh) er frekvensavhengig, kalles den følsomhetsfunksjonen.

Som følger av (10),

La oss introdusere notasjonen:

Verdien T kalles den komplementære (ekstra) sensitivitetsfunksjonen, siden S + T = 1. Følsomhetsfunksjonen lar deg evaluere endringen i egenskapene til systemet etter at tilbakemeldingen er lukket. Siden overføringsfunksjonen til et åpent system er lik G = PR, og til et lukket system Gcl = PR/(1+PR), så er forholdet deres Gcl/G = S. På samme måte, for et åpent system, er overføringsfunksjonen fra inngangen til forstyrrelser d til utgangen av et lukket system er (se ) P(s)/(1 + P(s)R(s)), og åpen sløyfe er P(s), så deres forhold er også S. For overføringsfunksjonen fra målestøyinngangen n til systemutgangen kan samme forhold oppnås S.

Ved å kjenne til formen til funksjonen S(jw) (for eksempel figur 18), kan vi si hvordan undertrykkelsen av ytre påvirkninger på systemet vil endre seg for forskjellige frekvenser etter at tilbakekoblingssløyfen er lukket. Det er klart at støyene ligger i frekvensområdet der |S(jш)| > 1, etter lukking vil tilbakemeldingen øke, og støyen med frekvenser der |S(jш)|< 1, после замыкания обратной связи будут ослаблены.

Det verste tilfellet (den største forsterkningen av ytre påvirkninger) vil bli observert ved den maksimale frekvensen Ms av modulen til følsomhetsfunksjonen (Figur 18):

Maksimum av sensitivitetsfunksjonen kan relateres til stabilitetsmarginen sm (Figur 15). For dette tar vi hensyn til at |1 + G(jш)| representerer avstanden fra punktet [-1, j0] til gjeldende punkt på hodografen til funksjonen G(jш). Derfor er minimumsavstanden fra punktet [-1, j0] til

funksjon G(jш) er lik:

Ved å sammenligne (13) og (14), kan vi konkludere med at sm = 1/Ms. Hvis modulen G(jsh) avtar med økende frekvens, vil (1-sm) ? 1/g. Ved å erstatte forholdet sm = 1/Ms her, får vi et estimat av forsterkningsmarginen uttrykt som maksimum av følsomhetsfunksjonen:

På samme måte, men med grovere forutsetninger, kan vi skrive fasemarginestimatet i form av maksimum av følsomhetsfunksjonen:

For eksempel, for Ms = 2 får vi gm ? 2 og? 29°.

Figur 18 - Følsomhetsfunksjoner for systemet med hodografer vist i figur 13

Robusthet er et systems evne til å opprettholde en gitt stabilitetsmargin med variasjoner i parametere forårsaket av en endring i belastning (for eksempel når ovnsbelastningen endres, endres tidskonstantene), teknologisk spredning av parametere og deres aldring, ytre påvirkninger , regnefeil og objektmodellfeil. Ved å bruke begrepet sensitivitet kan vi si at robusthet er en lav følsomhet av stabilitetsmarginen for variasjoner i parametrene til et objekt.

Hvis parametrene til objektet endres innenfor små grenser, når det er mulig å bruke erstatning av differensialen med et begrenset inkrement, kan effekten av endringer i parametrene til objektet på overføringsfunksjonen til det lukkede systemet estimeres ved å bruke følsomhetsfunksjon (10). Spesielt kan det konkluderes med at ved de frekvensene hvor modulen til følsomhetsfunksjonen er liten, vil effekten av endringer i objektparametrene på overføringsfunksjonen til et lukket system og følgelig på stabilitetsmarginen være liten.

For å vurdere virkningen av store endringer i parametrene til objektet, representerer vi overføringsfunksjonen til objektet i form av to termer:

P = P0 + DP, (17)

hvor P0 er den beregnede overføringsfunksjonen, er DP avviket fra P0, som må være en stabil overføringsfunksjon. Da kan sløyfeforsterkningen til et åpent system representeres som G = RP0 + RDP = G0 + RDP. Siden avstanden fra punktet [-1, j0] til det nåværende punktet A på hodografen til det uforstyrrede systemet (hvor DP = 0) er lik |1 + G0| (Figur 19), stabilitetsbetingelsen for et system med sløyfeforsterkningsavvik RDP kan representeres som:

|RDP|< |1+G0|,

hvor T er en ekstra sensitivitetsfunksjon (12). Til slutt kan vi skrive forholdet:

som må oppfylles for at systemet skal forbli stabilt når prosessparametrene endres med verdien av DP(jsh).

Reduksjon av nuller og poler. Siden overføringsfunksjonen med åpen sløyfe G = RP er produktet av to overføringsfunksjoner, som i generell sak har både en teller og en nevner, så er det mulig å annullere polene som ligger i høyre halvplan eller er nærme det. Siden under reelle forhold, når det er spredning av parametere, utføres en slik reduksjon unøyaktig, kan det oppstå en situasjon når en teoretisk analyse fører til konklusjonen at systemet er stabilt, men faktisk med et lite avvik i prosessparametrene fra de beregnede verdiene blir den ustabil.

Derfor, hver gang når polene reduseres, er det nødvendig å sjekke stabiliteten til systemet med en reell spredning av objektets parametere.

Figur 19 - Forklaring av utledningen av forholdet (18)

Den andre effekten av forkortningen av polene er utseendet til en betydelig forskjell mellom innreguleringstiden for den forbigående prosessen i et lukket system under påvirkning av et settpunktsignal og eksterne forstyrrelser. Derfor er det nødvendig å kontrollere responsen til den syntetiserte kontrolleren under påvirkning av ikke bare settpunktsignalet, men også eksterne forstyrrelser.

Støtfri veksling av kontrollmoduser. I PID-kontrollere kan det være moduser når parametrene deres endres brått. For eksempel når det er nødvendig å endre integrasjonskonstanten i et kjørende system eller når det etter manuell kontroll av systemet er nødvendig å bytte til automatisk modus. I de beskrevne tilfellene kan det oppstå uønskede overskridelser av den kontrollerte variabelen dersom spesielle tiltak ikke iverksettes. Derfor oppstår problemet med jevn (“støtfri”) bytting av driftsmoduser eller kontrollerparametere. Hovedmetoden for å løse problemet er å bygge en slik kontrollerstruktur, når parameterendringen utføres før integrasjonsstadiet. For eksempel, med en skiftende parameter Ti = Ti (t), kan integralleddet skrives i to former:

I(t) = eller I(t) = .

I det første tilfellet, når Ti (t) endres brått, vil integralleddet endres brått, i det andre tilfellet vil det endre seg jevnt, siden Ti (t) er under integraltegnet, hvis verdi ikke kan endres brått.

En lignende metode er implementert i den inkrementelle formen til PID-kontrolleren (se avsnittet "Inkrementell form for den digitale PID-kontrolleren") og i serieformen til PID-kontrolleren, hvor integrasjonen utføres i sluttfasen av kontrollberegningen.

2.2 Diskret kontroller fra digital PID-kontrollerligning

Kontinuerlige variabler er praktiske å bruke for analyse og syntese av PID-kontrollere. For teknisk implementering er det nødvendig å bytte til en diskret form for ligninger, siden grunnlaget for alle kontrollere er en mikrokontroller, kontroller eller datamaskin som opererer med variabler hentet fra analoge signaler etter deres tidskvantisering og nivåsampling.

På grunn av den endelige tiden for beregning av kontrollhandlingen i mikrokontrolleren og forsinkelsen i analog-til-digital konvertering mellom øyeblikket det analoge signalet kommer til inngangen til kontrolleren og utseendet til kontrollhandlingen ved utgangen, en uønsket forsinkelse vises, noe som øker den totale forsinkelsen i kontrollsløyfen og reduserer stabilitetsmarginen.

Hovedeffekten som vises under sampling og som ofte "gjenoppdages" er utseendet til aliasfrekvenser i spekteret til det kvantiserte signalet i tilfellet når kvantiseringsfrekvensen ikke er høy nok.

En lignende effekt oppstår når du filmer et spinnende bilhjul. Frekvensen til aliassignalet er lik forskjellen mellom interferensfrekvensen og kvantiseringsfrekvensen. I dette tilfellet blir høyfrekvente interferenssignalet forskjøvet til lavfrekvente regionen, hvor det legges over det nyttige signalet og skaper store problemer, siden det er umulig å filtrere det på dette stadiet.

For å eliminere aliaseffekten er det nødvendig å installere et analogt filter før inngangen til analog-til-digital-omformeren, som vil dempe støyen med minst en størrelsesorden ved en frekvens som tilsvarer halvparten av kvantiseringsfrekvensen. Vanligvis brukes et Butterworth-filter av andre eller høyere orden. Den andre løsningen på problemet er å øke kvantiseringsfrekvensen slik at den er minst 2 ganger (ifølge Kotelnikov-teoremet) høyere enn den maksimale frekvensen til støyspekteret. Dette gjør at et digitalt lavpassfilter kan brukes etter kvantisering. Med en slik samplingshastighet er det mottatte digitale signalet helt ekvivalent med det analoge når det gjelder mengden informasjon, og alle egenskapene til den analoge kontrolleren kan utvides til den digitale.

Overgang til endelige forskjellsligninger. Overgangen til diskrete variabler i de analoge kontrollerlikningene utføres ved å erstatte derivater og integraler med deres diskrete motstykker. Hvis ligningen er skrevet i operatorform, blir det først gjort en overgang fra bildeområdet til det opprinnelige området. I dette tilfellet erstattes differensieringsoperatoren med en derivert, integrasjonsoperatoren erstattes av en integral.

Det er mange måter å tilnærme derivater og integraler etter deres diskrete motstykker, som er skissert i kursene om numeriske metoder for å løse differensialligninger. I PID-kontrollere er de mest vanlige de enkleste typene tilnærming av den deriverte med en endelig forskjell og integralet med en endelig sum. Tenk på integreringsleddet til PID-kontrolleren:

Å skille begge deler med hensyn til tid, får vi

Ved å erstatte differensialene i dette uttrykket med endelige forskjeller (venstre forskjeller), får vi

der indeksen i betyr at den gitte verdien ble tatt på tidspunkt ti (merk at her og under indeksen i i Ti angir ikke nummeret på tidstrinnet, men integral koeffisient PID-kontroller). Fra det siste uttrykket får vi:

Dermed kan neste verdi av integralet beregnes ved å kjenne den forrige og verdien av feilen ved forrige gang. En slik formel har imidlertid en tendens til å akkumulere en regnefeil over tid hvis forholdet Dt/Ti ikke er lite nok. En annen integrasjonsformel er mer stabil - med riktige forskjeller, når feilverdien tas samtidig med det beregnede integralet:

Tenk på differensialbegrepet til en PID-kontroller med et filter:

Ved å overføre denne formelen fra bilder til originaler får vi:

Ved å erstatte differensialene med endelige inkrementer får vi differanseligningen:

Merk at for konvergensen av den iterative prosessen (21) er det nødvendig at

Når Dt > Td/N, blir den iterative prosessen (21) oscillerende, noe som er uakseptabelt for PID-kontrolleren. Differanseligningen oppnådd ved å bruke de riktige forskjellene har de beste egenskapene:

Her er konvergensbetingelsen oppfylt for alle Dt, og ingen svingninger forekommer for noen verdier av parameterne. I tillegg lar den siste formelen deg "slå av" differensialkomponenten i PID-regulatoren ved å sette Td = 0, noe som ikke kan gjøres i uttrykk (21), siden deling med null forekommer i dette tilfellet. Du kan bruke enda mer presise formler for numerisk differensiering og integrasjon, kjent fra løpet av numeriske metoder for å løse likninger. Verdien av kvantiseringssyklusen Dt velges så liten som mulig, dette forbedrer kvaliteten på reguleringen. For å sikre god reguleringskvalitet bør den ikke være mer enn 1/15...1/6 av tidspunktet for etablering av objektets transiente respons på nivået 0,95 eller 1/4...1/6 av verdien av transportforsinkelsen. Imidlertid, med en økning i kvantiseringsfrekvensen med mer enn 2 ganger sammenlignet med den øvre frekvensen av spekteret av forstyrrende signaler (i henhold til Kotelnikov-teoremet), er det ingen ytterligere forbedring i reguleringskvaliteten.

Hvis det ikke er et anti-aliasfilter ved regulatorinngangen, velges kvantiseringsfrekvensen 2 ganger høyere enn den øvre grensefrekvensen til støyspekteret for å bruke digital filtrering. Det bør også tas i betraktning at den utøvende enheten må ha tid til å trene i løpet av tiden Dt.

Hvis kontrolleren ikke bare brukes til regulering, men også for alarmsignalering, kan ikke kvantiseringssyklusen være mindre enn den tillatte forsinkelsen for driften av alarmsignalet.

Med en liten kvantiseringssyklus øker feilen ved beregning av den deriverte. For å redusere det, kan du bruke utjevningen av de mottatte dataene på flere innsamlede punkter før differensieringsstadiet.

Digital PID-kontrollerligning. Basert på ovenstående kan den diskrete PID-kontrollerligningen skrives som:

hvor i er nummeret på tidstrinnet.

For å starte algoritmen velger vi vanligvis uD0 = 0, I0 = 0, e0 = 0, men det kan være andre Innledende forhold, avhengig av betydningen av et spesifikt kontrollproblem.

Merk at algoritmen oppnådd ved ganske enkelt å erstatte differensierings- og integrasjonsoperatørene i den klassiske PID-kontrollerligningen

sluttdifferanser og sluttsummer

har dårlig stabilitet og lav nøyaktighet, som vist tidligere. Men etter hvert som samplingsfrekvensen øker, slettes forskjellen mellom de to ovennevnte algoritmene.

Inkrementell form av en digital PID-kontroller. Ganske ofte, spesielt i nevrale nettverk og fuzzy-kontrollere, brukes PID-kontrollerligningen i form av en avhengighet av inkrementet til kontrollvariabelen på kontrollfeilen og dens deriverte (uten en integrert term). Denne representasjonen er praktisk når en ekstern enhet spiller rollen som en integrator, for eksempel en konvensjonell eller trinnmotor . Rotasjonsvinkelen til dens akse er proporsjonal med verdien av kontrollsignalet og tiden. I fuzzy-kontrollere, når en ekspert formulerer uklare regler, kan en ekspert formulere avhengigheten til kontrollvariabelen av den deriverte verdien, men han kan ikke formulere avhengigheten av integralverdien, siden integralet "husker" hele historien til feilendringen, som en person kan ikke huske.

Den inkrementelle formen til PID-kontrolleren oppnås ved å differensiere ligningen (25):

For å oppnå en null kontrollfeil, må en integrator installeres ved utgangen til den inkrementelle kontrolleren (Figur 20):

Figur 20 - Inkrementell form av PID-kontrolleren

Ved å sende inn de oppnådde uttrykkene til endelige forskjeller, får vi den diskrete formen til den inkrementelle PID-kontrolleren:

hvor Dui+1 = ui+1 - ui;

Dei = ei - ei-1.

En mer stabil og nøyaktig differanseligning kan oppnås ved å erstatte uttrykk for ui+1 og ui fra (24) i formelen Dui+1 = ui+1 - ui.

Den inkrementelle formen til kontrolleren er praktisk for bruk i mikrokontrollere, siden hoveddelen av beregningene i den utføres i trinn, som kan representeres av et ord med et lite antall binære sifre. For å få ut verdien av kontrollvariabelen kan du utføre kumulativ summering på sluttfasen av beregningene: ui+1 = ui + Dui+1.

Før du beregner parametrene til kontrolleren, er det nødvendig å formulere målet og kriteriene for kvaliteten på reguleringen, samt begrensninger på størrelsen og endringshastigheten til variabler i systemet. Tradisjonelt er hovedkvalitetsindikatorene formulert ut fra kravene til formen for responsen til et lukket system på en trinnendring i settpunktet. Dette kriteriet er imidlertid svært begrenset. Spesielt sier det ikke noe om mengden av demping av målestøy eller påvirkning av eksterne forstyrrelser; det kan gi en feilaktig ide om systemets robusthet.

Derfor, for å fullstendig beskrive eller teste et system med en PID-kontroller, er det nødvendig med en rekke ekstra kvalitetsindikatorer, som vil bli diskutert senere.

I det generelle tilfellet kan valget av kvalitetsindikatorer ikke formaliseres fullstendig og må utføres basert på betydningen av problemet som skal løses.

3. Regulatorisk kvalitet

3.1 Ytelseskriterier Dempning av påvirkning av ytre forstyrrelser

Valget av kontrollkvalitetskriterium avhenger av formålet regulatoren brukes til. Målet kan være:

Opprettholde en konstant verdi av en parameter (for eksempel temperatur);

Settpunktsporing eller programvarekontroll;

Spjeldstyring i væsketank o.l.

For en bestemt oppgave kan den viktigste faktoren være:

Form for respons på eksterne forstyrrelser (avgjørelsestid, overskridelse, responstid osv.);

Form av respons på målestøy;

Form for respons på settpunktsignalet;

Robusthet i forhold til spredningen av parametrene til kontrollobjektet;

Spare energi i et kontrollert system;

Minimering av målestøy.

For en klassisk PID-regulator er parametrene som er best for å overvåke settpunktet generelt forskjellige fra parametrene som er best for å dempe påvirkningen av eksterne forstyrrelser. For at begge parameterne skal være optimale samtidig, er det nødvendig å bruke PID-regulatorer med to frihetsgrader.

Nøyaktig sporing av settpunktsendringer er nødvendig i bevegelseskontrollsystemer, i robotikk; i prosesskontrollsystemer, hvor settpunktet vanligvis forblir uendret i lang tid, kreves maksimal dempning av påvirkningen fra lasten (eksterne forstyrrelser); i væskereservoarkontrollsystemer er det nødvendig å sikre den laminære strømningen (minimering av variansen til utgangsvariabelen til regulatoren), etc.

Som vist i underavsnittet, svekker tilbakemelding påvirkningen av ytre forstyrrelser i |S(jш)| ganger, bortsett fra de frekvensene der |S(jw)|. Eksterne forstyrrelser kan påføres et objekt i mange forskjellige deler av det, men når den spesifikke plasseringen er ukjent, anses forstyrrelsen å virke på objektets inngang. I dette tilfellet bestemmes systemets respons på eksterne forstyrrelser av overføringsfunksjonen fra inngangen til eksterne forstyrrelser til systemutgangen:

Siden ytre forstyrrelser vanligvis ligger i den lavfrekvente delen av spekteret, hvor |S(jш)| og, følgelig, T, så kan uttrykk (28) forenkles:

For å svekke påvirkningen av ytre forstyrrelser (spesielt påvirkningen av belastningen), kan man redusere integrasjonskonstanten Ti.

I tidsdomenet estimeres responsen på eksterne forstyrrelser fra responsen på et enkelt hopp d(t). Redusere effekten av målestøy: Overføringsfunksjonen fra punktet for påføring av støy til systemutgangen er:

På grunn av nedgangen i frekvensresponsen til objektet med høye frekvenser sensitivitetsfunksjonen har en tendens til 1 (Figur 18). Derfor er det umulig å redusere effekten av målestøy ved hjelp av tilbakemelding. Imidlertid elimineres disse støyene lett ved bruk av lavpassfiltre og riktig skjerming og jording.

Det lukkede systemet forblir stabilt når objektparametrene endres med verdien av DP(jw), hvis betingelsen (18) er oppfylt.

Kvalitetskriterier i tidsdomenet. For å vurdere kvaliteten på reguleringen i et lukket system med en PID-kontroller, brukes vanligvis en trinnvis inngangshandling og en rekke kriterier for å beskrive formen på den forbigående prosessen (Figur 21):

Maksimal kontrollfeil

og tidspunktet Tmax da feilen når dette maksimum;

Integrert absolutt feil

Integral av kvadratfeil

Reduser d (dette er forholdet mellom det første maksimumet og det andre, typiske verdien d=4 eller mer)

vi legger merke til at andre definisjoner av dempingsreduksjonen også finnes i litteraturen, spesielt, som eller som b/a-koeffisienten i eksponenten til eksponenten som beskriver omhyllingen av dempede oscillasjoner;

Statisk feil e0 (dette er en konstant feil i likevekten, det vil si i den jevne eller statiske modusen til systemet);

Settingstid Te med en gitt feil es (dette er tiden etter hvilken kontrollfeilen ikke overskrider den innstilte verdien es; vanligvis es = 1 %, sjeldnere 2 % eller 5 % - henholdsvis utligningstiden er betegnet med T0. 01, T0,02, T0,05);

Overshoot emax (dette er overskuddet av den første toppen over steady state-verdien til variabelen, vanligvis uttrykt som en prosentandel av steady state-verdien);

Stigetid Tr (dette er tidsintervallet der utgangsvariabelen stiger fra 10 til 90 % av dens stabile verdi);

Perioden med dempede svingninger Tcl (strengt tatt er dempede svingninger ikke periodiske, derfor forstås her perioden som avstanden mellom to tilstøtende maksima av transientkarakteristikken).

Figur 21 - Kriterier for reguleringskvalitet i tidsdomenet

For bevegelseskontrollsystemer brukes rampefunksjonen oftere som et testsignal enn hoppfunksjonen, siden elektromekaniske systemer vanligvis har en begrenset svinghastighet på utgangsverdien.

Kriteriene ovenfor brukes for å vurdere kvaliteten på responsen både på settpunktsendringer og påvirkningen av eksterne forstyrrelser og målestøy.

Kvalitetskriterier for frekvens. I frekvensdomenet brukes vanligvis følgende kriterier, hentet fra plottet av amplitude-frekvensresponsen til et lukket system y (u) (Figur 22):

Båndbredde u-3dB (eller u0.7) på nivået -3 dB (eller på nivået 1/ = 0.7) - frekvensbånd fra 0 til u-3dB = u0.7, innenfor hvilket frekvensresponskurven synker med ingen mer enn 3 dB i forhold til verdien ved null frekvens y(0);

Oscillation M - forholdet mellom den maksimale (topp) verdien av frekvensresponsen ymax og dens verdi ved null frekvens y(0), det vil si i stabil tilstand

typiske verdier er M = 1,5...1,6;

Resonansfrekvensen til systemet wp er frekvensen som frekvensresponsen når sin maksimale ymax = y(wp).

Frekvenskriteriene til reelle regulatorer kan ikke entydig relateres til tidskriteriene på grunn av ikke-lineariteter (vanligvis er disse "begrensende" ikke-lineariteter) og algoritmer for å eliminere den integrerte metningseffekten. Det er imidlertid tilnærmet mulig å etablere følgende sammenhenger mellom kriteriene i frekvens- og tidsdomenene:

Frekvensen til den maksimale overføringskarakteristikken til et lukket system tilsvarer omtrent perioden med dempede oscillasjoner av responsen til den trinnvise inngangen - h;

Jo langsommere vibrasjonene avtar, desto større er oscillerende indeks M.

Valg av kontrollerparametere. PÅ generell teori automatisk kontroll strukturen til kontrolleren velges basert på modellen til kontrollobjektet. I dette tilfellet tilsvarer mer komplekse kontrollobjekter mer komplekse kontroller. I vårt tilfelle er kontrollerstrukturen allerede satt - vi vurderer en PID-kontroller. Denne strukturen er veldig enkel, så PID-regulatoren kan ikke alltid gi god kvalitet kontroll, selv om PID-kontrollere brukes i de aller fleste industrielle applikasjoner.

Lignende dokumenter

Typer og bruk av sensorer automatisk kontroll regimeparametre for teknologiske prosesser kjemisk produksjon. Prinsippet for drift av målte sensorer, temperaturkontrollere, modulære brytere. Midler for beskyttelse av elektriske installasjoner.

avhandling, lagt til 26.04.2014


Bekjentskap med stadiene for å beregne innstillingene til typiske regulatorer i et enkeltsløyfe automatisk responssystem. Funksjoner ved valg av type industriell regulator. Metoder for å konstruere stabilitetsregionen i planet for kontrollerens innstillingsparametere.

avhandling, lagt til 17.06.2013


Analyse av reguleringsobjektets egenskaper, typiske regulatorer og valg av type regulator. Beregning av optimale parametere for kontrollerinnstillinger. Avhengighet av den regulatoriske handlingen av avviket til den kontrollerte verdien. Integrerte og proporsjonale regulatorer.

semesteroppgave, lagt til 02.11.2014


Designe en enhet som måler temperaturen i et rom. Valg av temperatursensor, mikrokontroller og feilsøkingstavle. Studerer driften av den innebygde temperatursensoren. Programvare utvikling. Funksjonell organisering av programmet.

semesteroppgave, lagt til 26.12.2013


Designe en elektrisk motormodell med beregnede parametere i Simulink-miljøet. Simulering av motordrift med ulike belastninger (forstyrrende dreiemoment). Beregning av parametere og optimale kontrollere og kvalitetsindikatorer for en rekke egenskaper.

semesteroppgave, lagt til 24.06.2012


Beregning av den komplekse frekvensresponsen til objektet i det nødvendige frekvensområdet. Bestemmelse av stabilitetsmarginen til en lukket automatisk system regulering. Evaluering av kontrollkvaliteten ved bruk av PI- og PID-regulatorer og valg av den beste.

semesteroppgave, lagt til 04.12.2014


Akselererende karakteristikk av objektet for regulering og bestemmelse av parametere som karakteriserer treghetsegenskapene til objektet. Beregning av innstillingene til regulatorer i henhold til amplitude-fasekarakteristikken til det regulerte objektet. Beregning av ATS kvalitetsindikatorer.

semesteroppgave, lagt til 22.10.2012


Syntese av en proporsjonal-integral-differensialkontroller som gir indikatorer på nøyaktighet og kontrollkvalitet for et lukket system. Amplitude-frekvenskarakteristikk, dynamisk analyse og den forbigående prosessen til det justerte systemet.

semesteroppgave, lagt til 08.06.2013


Beregning av PI-kontroller tuning parametere for et andre-ordens objekt. Analytisk beregning og implementering av programmet i MatLab-miljøet, som bestemmer parametrene til kontrolleren og transienten. Kriterier for kvaliteten på den forbigående prosessen i et lukket system.

laboratoriearbeid, lagt til 29.09.2016


Klassifisering av elektromagnetiske suspensjoner. Bygge en matematisk modell av stativet. Programvareimplementering av en proporsjonal-integral-differensialkontroller. Beskrivelse av ATmega 328-mikrokontrolleren og Arduino-kortet. Montering og igangkjøring av stand.

• opplæringen

PID-kontrolleren er den enkleste kontrolleren som har effektive analoge maskinvareimplementeringer og er derfor den mest brukte. For arbeidet krever det å sette 3 koeffisienter for et spesifikt objekt, slik at du kan velge reguleringsprosessen i henhold til kravene. Med en enkel fysisk betydning og en enkel matematisk notasjon, er den mye og ofte brukt i temperaturregulatorer, gassstrømregulatorer og andre systemer der det er nødvendig å opprettholde en viss parameter på et gitt nivå, med mulige overganger mellom forskjellige forhåndsinnstilte nivåer. Selvfølgelig er det mer komplekse kontrollere som lar deg nå de innstilte parametrene mer nøyaktig og raskere og med mindre oversving, i tillegg til å ta hensyn til ikke-lineariteten eller hysteresen til det kontrollerte objektet, men de har større beregningskompleksitet og er vanskeligere å sette opp.

Til tross for sin enkelhet med både fysisk betydning og matematisk notasjon:

I programvareimplementeringen av PID-kontrolleren gjøres det ofte feil som oppstår selv i verifiserte automatiseringsenheter.

Dessuten er det ekstremt enkelt å kontrollere kvaliteten på implementeringen av PID-kontrolleren.

Ta i betraktning det enkleste eksempelet: termostat. For å teste kvaliteten er et raskt objekt med lav treghet og lavt strømforbruk best egnet. En klassiker av sjangeren: en vanlig 100W lyspære med et tynt termoelement (XA) skrudd fast. Og den første tingen å sjekke PID-kontrolleren er degraderingen av PID til bare en P-kontroller. Det vil si at vi setter integral- og differensialkoeffisienten til null, og setter proporsjonalen til maksimum.

Vi slår på regulatoren, sjekk: gjeldende temperatur er 22 grader, innstillingen er 16 grader. Lampen lyser ikke. Vi begynner å begynne å øke innstillingen: 16.1, 16.3, 16.7, 18 ... 19 ... lyset er på. Som?! Hvor?! Vi stopper - slått av. Så vi møttes første klassiske feil implementering av PID-kontrolleren.

En liten matematisk digresjon: la oss igjen huske integralnotasjonen angitt ovenfor. Vi implementerer det programmatisk, som betyr diskret. Det vil si at vi med misunnelsesverdig regularitet måler inngangsverdien, sammenligner den med settpunktet, beregner effekten, utsteder, gjentar. Så det er nødvendig å gå fra den integrerte formen til den endelige forskjellsordningen. Ved overgang brukes vanligvis en front-mot-overgang:

hvor E(n) = X(n) - X0(n) - det vil si størrelsen på misforholdet mellom gjeldende og innstilte verdi for den kontrollerte parameteren.

Bruken av en direkte formel vil for det første kreve å beregne og lagre integralet av mistilpasninger over en lang periode, og for det andre vil det kreve flytepunktarbeid med høy presisjon (siden integralkoeffisienten Ki er alltid< 1), либо операции деления (представляя коэффициент в форме 1/Ki) большой разрядности. Всё это требует вычислительных ресурсов, коих в embedded как правило сильно ограничено… Поэтому, вместо реализации прямой схемы, реализуют рекуррентную формулу:

bruken av en rekursiv formel gjør det mulig å redusere mengden av beregninger og bitdybden til mellomverdier.

Så tilbake til kontrolleren vår. Så det er et justerbart objekt: en lyspære. For å kontrollere strømmen som leveres til den, brukes en enkel tilnærming: strømforsyningen (220V 50Hz) mates gjennom triacen til lasten. Triacen slår seg av i det øyeblikket halvbølgen passerer gjennom null, og forblir av til et signal tilføres kontrollelektroden. Jo tidligere etter begynnelsen av halvbølgen vi gir et kontrollsignal, jo mer energi fra denne halvbølgen vil nå det kontrollerte objektet. Ved riktig timing av lineariteten til halvbølgeområdet fra tid X til slutten av halvbølgen, er vi i stand til å gi ut effekt fra 0 til 100 % med nøyaktigheten som vi beregnet lineariseringstabellen med.

Så vi kan gi effekt fra 0 til 100%. I virkelige gjenstander er det ofte umulig å gi ut 100% strøm - for eksempel er dette full av utbrenthet av varmeelementet. Derfor har alle enheter en innstilling for minimum og maksimum utgangseffekt per objekt.

Så, etter å ha beregnet U(n) i henhold til formelen ovenfor, legges en annen begrensning av resultatet til:
hvis Un< Umin then Un:= Umin; if Un>Umax deretter Un:= Umax;
Etter det er den beregnede Un den nødvendige utgangseffekten for øyeblikket. Ta-dam! Det er denne implementeringen som skaper feilen beskrevet ovenfor.

Årsaken er banal: i overgangsøyeblikket fra et diskret til et endelig forskjellsskjema, "braketter" vi operasjonen for å beregne integralet, og ved hvert trinn legger vi den deriverte til den akkumulerte summen U(n-1) . Etter å ha pålagt en begrensning på det, annullerer vi faktisk hele det beregnede integralet. (Vel, ikke hvor mye vi tilbakestiller, hvor mye vi bringer til området 0-100, som i dette tilfellet ikke er signifikant). Dermed differensierer vi PID-kontrolleren, og differensialakseleratoren forblir. Det som faktisk ser ut som en enkel differensialregulator - kraften tilføres proporsjonalt med endringen i settpunktet eller den kontrollerte variabelen, og ikke proporsjonalt med differansen mellom settpunktet og den kontrollerte variabelen.

Konklusjon #1: Beregningen av U(n) kan ikke begrenses. For å begrense strømtilførselen til utgangsenheten, bør en egen variabel stilles inn.

Nå som vi har fått Urn, for begrenset kraft, laster vi opp på nytt, vi fortsetter å teste.
Vi slår på regulatoren, sjekk: gjeldende temperatur er 22 grader, innstillingen er 16 grader. Lampen lyser ikke.
Vi begynner å legge til innstillingen: 16.1, 16.4, 17, 18, 20, 22, 24 (oops! lyser opp! hurra!), 28, 30, 40, 60 ... Skjønnhet! Arbeider!
Vi følger med på prosessen – det viste seg å være rundt 60, det dingler litt frem og tilbake, men det holder. Det ser ut til at alt er vakkert. Vi puster ut, vi sjekker kontrollen fra PC-en: vi setter 600 grader. Og... Lyset slår seg av. Hvordan det? Settpunkt 600, strøm 60, men lyset er av?

Mens vi venter og sakte innser at vi tydelig har vært borti noen "Classic Joint #2"™ lyspæren blusser sakte opp, går til 100 % effekt, og forblir slik - den kan ikke gi ut 600 grader.

Vi går tilbake til forskjellsordningen vår. U(n) = U(n-1) + Kp*(dE + ...) . Restdifferansen multiplisert med proporsjonalitetskoeffisienten legges til den nåværende beregnede verdien av påvirkningen. Vi hadde et settpunkt på 60, ​​en temperatur på 60, ​​det vil si null avvik. Utgangseffekten var også null. Og på en gang, brått, ble settpunktet økt til 600 grader. avviket ble kraftig 540 grader, de multipliserte det også med proporsjonalitetsfaktoren ... og fløy ut av U (n) lagringskapasiteten. Ikke le, bruk fastpunktmatematikk i stedet for flytende komma. Med en forskjell på 540 grader og arbeid gjennom 1/16, med en proporsjonalitetsfaktor på 20, får vi ... 540 * 20 * 16 = 172800, og hvis vi har en 16-bit U (n), og til og med et fortegn en, så faktisk, som et resultat av beregningen, fikk vi A300h = -8960. Opachki. I stedet for et stort pluss - et håndgripelig slikt minus.

Konklusjon #2: Beregninger må gjøres med korrekt overløpsstøtte. Overfylt? Begrens grensetallet, absolutt ikke pakk inn.

Så vi økte bitdybden U (n), oversatte på nytt, sydde opp, vi lanserer. Lyspæren er ikke helt avkjølt enda, det er 80 grader der, innstillingen er fortsatt den samme 600. Lyspæren lyser ... og slukker. Den lyser og slukker. Hvordan det? Innstillingen er 600, lyspæren er 80 - og den holder sine egne 80 ganske bra! Hvordan er det?! Klart vi kom oss ut Feil #3.

Og igjen, en lyrisk-matematisk digresjon. Så, det er vårt forskjellsskjema: U(n) = G(U(n-1), dE(n)) . Nok en gang: den nye verdien av påvirkningen er summen av tidligere påvirkning og en viss påvirkning, avhengig av forskjellen mellom gjenværende på det nåværende tidspunkt og den forrige. Hva er forrige øyeblikk? Og hva er det forrige øyeblikket til det forrige? Vel, husk skolen. Bevis ved induksjon. Hvis det er mulig å konstruere et bevis for K+1, forutsatt at beviset for K er riktig, Og bevis separat hva som er sant for K=0, så er beviset sant. Så hvordan beregner vi U(0)?

En vanlig løsning: tilbakestill alt, les settpunktet fra flashminnet og settpunktene, vent på 1 pollingsyklus og les X(0). Her er null klar, nå jobber vi. Og... Og ikke riktig. Hvorfor? Fordi den tilbakevendende formelen frastøtes av endringer i residuet. Og etter å ha initialisert med null og lastet inn gjeldende verdier, har vi mistet startbetingelsene. Det er det - i stedet for å holde den absolutte temperaturverdien på et nivå lik det absolutte settpunktet, begynner regulatoren å holde temperaturen lik starttemperaturen pluss settpunktdifferansen. Det vil si at det var 80 grader og innstillingen var 200, slått på enheten - den holder 80. Endret innstillingen til 240 - den begynte å holde 120.

Riktig initialisering av differanseskjemaet: sett _alt_ til null. Det er
X(0) = 0, X0(0) = 0. U(0) = 0. E(0)=X(0)-X0(0)=0.
Og på den aller første syklusen med beregninger, vises settpunktet og gjeldende verdi, som det var, brått:
X(1) = 80. X0(1)=200. U(1) = U(0)+Kp*(E(1)-E(0)) = U(0)+Kp*(X(1)-X0(1)-E(0)) = 0 + 20*(200 - 80 - 0) = 2400
Nå fungerer kretsen som den skal.

Konklusjon #3: initialiser startforholdene på riktig måte.

Er det riktig? Vel, vel, vel ... Nok en gang ... Vi setter innstillingen til 20. Vi venter på avkjøling ... Vi slår den av. Slå på. Så skjønnhet: strøm 20, settpunkt 20. Sett hopp 600. La oss bli varme. 100, 120 ... satt innstillingen til 20. Den slo seg av, den ble avkjølt. Vi venter litt (120… 110… 100… 90… 80…) og setter innstillingen til 100. La oss bli varme… 105 grader, slått av. Stoppe. Og hvorfor holder den 105? For oss er det nå bare den proporsjonale komponenten som fungerer. Med riktig implementering fra den fysiske betydningen av prosessen, kan ikke den oscillerende prosessen holde innstillingen høyere enn den er satt. strengt tatt under. Og den holder 5 grader mer enn spurt. Det er observert Prank #4.

Så la oss huske hva vi hadde ovenfor: Konklusjon #2: U(n) kan ikke begrenses. Og konklusjon nr. 3: ved overløp må du fortsatt begrense. Ja Ja. Ellers forskyves "arbeidspunktet" med et begrenset øyeblikk. Hva å gjøre? Øke rangeringen? Vel, hvis det er nok datakraft. Er det nødvendig? Hva er egentlig galt med å ha U(n) = 9999,99 og ikke 29999,99? Generelt bare at vi mistet 20 000. Men nå, for å jobbe, trenger vi bare å falle inn 100 % av kraften uansett, ikke sant? Riktig. Det betyr at det ikke er noe problem med restriksjonen i regimentet, så lenge vi ikke går bort fra grensen. I tilfelle overløp må det derfor settes et flagg, og når for eksempel halvparten av området (det vil si ettersom U(n) etter 9999.9 falt under 5000.00) når man når for eksempel, må kretsen startes på nytt. Det vil si forkast historikk, si at n=0 og se konklusjon nr. 3 ovenfor. Et nysgjerrig sinn har allerede innsett det i saken komplett opplegg, når alle tre komponentene ikke er lik null, og nullstiller den iterative prosessen i prosessen, nulliserer vi også det akkumulerte integralet til integralkomponenten. Men på grunn av det faktum at vi tilbakestiller til null mye på forhånd, vil det ha tid til å samle seg i løpet av tiden for ekstra produksjon av resten. Og det er ikke helt riktig å akkumulere integralet på "store" trinn, siden hensikten med integralkomponenten er å "velge" avviket at proporsjonalkomponenten ikke kan løses separat.

Konklusjon #4: hvis U(n) av en eller annen grunn var begrenset, bør kretsen initialiseres på nytt så snart kretsen så ut til å være normal igjen.

I neste nummer: er det nødvendig å implementere en differanseordning? En detaljert implementering av en direkte diskret krets med enkle og forståelige justerbare koeffisienter, med en direkte fysisk betydning, som enkelt beregner kontrollhandlingen ved en frekvens på 25Hz på ADuC847-prosessoren (rask 8-bits kontroller, med 8051-kjernen), og forlater mye CPU-tid for andre prosesser.

(Bilder som viser formler er hentet fra artikkelen