Gauss-metoden, også kalt metoden for suksessiv eliminering av ukjente, består i følgende. Ved å bruke elementære transformasjoner bringes systemet med lineære ligninger til en slik form at matrisen av koeffisienter viser seg å være trapesformet (samme som trekantet eller trinnformet) eller nær trapesformet (det direkte forløpet til Gauss-metoden, da - bare et direkte trekk). Et eksempel på et slikt system og dets løsning er vist i figuren ovenfor.

I et slikt system inneholder den siste ligningen bare én variabel, og verdien kan finnes unikt. Deretter erstattes verdien av denne variabelen i den forrige ligningen ( Gaussisk revers , deretter - bare et omvendt trekk), hvorfra den forrige variabelen er funnet, og så videre.

I et trapesformet (trekantet) system, som vi ser, inneholder ikke lenger den tredje ligningen variabler y og x, og den andre ligningen - variabel x .

Etter at matrisen til systemet har fått en trapesformet form, er det ikke lenger vanskelig å sortere ut spørsmålet om systemets kompatibilitet, bestemme antall løsninger og finne løsningene selv.

Fordeler med metoden:

1. når man løser systemer med lineære ligninger med mer enn tre ligninger og ukjente, er Gauss-metoden ikke like tungvint som Cramer-metoden, siden det kreves færre beregninger når man løser Gauss-metoden;
2. ved hjelp av Gauss-metoden kan du løse ubestemte systemer av lineære ligninger, det vil si å ha en felles løsning (og vi vil analysere dem i denne leksjonen), og ved å bruke Cramer-metoden kan du bare konstatere at systemet er usikkert;
3. du kan løse systemer med lineære ligninger der antall ukjente ikke er lik antall ligninger (vi vil også analysere dem i denne leksjonen);
4. metoden er basert på elementære (skole) metoder - metoden for substitusjon av ukjente og metoden for å legge til ligninger, som vi berørte i den tilsvarende artikkelen.

For at alle skal være gjennomsyret av enkelheten som trapesformede (triangulære, trinn) systemer av lineære ligninger løses med, presenterer vi løsningen av et slikt system ved å bruke det omvendte slaget. En rask løsning på dette systemet ble vist på bildet i begynnelsen av leksjonen.

Eksempel 1 Løs et system med lineære ligninger ved å bruke det motsatte trekket:

Løsning. I dette trapesformede systemet er variabelen z er unikt funnet fra den tredje ligningen. Vi erstatter verdien av den i den andre ligningen og får verdien av variabelen y:

Nå vet vi verdiene til to variabler - z og y. Vi erstatter dem i den første ligningen og får verdien av variabelen x:

Fra de foregående trinnene skriver vi ut løsningen av ligningssystemet:

For å oppnå et slikt trapesformet system av lineære ligninger, som vi løste veldig enkelt, er det nødvendig å bruke en direkte bevegelse assosiert med elementære transformasjoner av systemet med lineære ligninger. Det er heller ikke veldig vanskelig.

Elementære transformasjoner av et system av lineære ligninger

Ved å gjenta skolemetoden for algebraisk addisjon av likningene til systemet fant vi ut at en annen likning av systemet kan legges til en av likningene i systemet, og hver av likningene kan multipliseres med noen tall. Som et resultat får vi et system med lineære ligninger som tilsvarer den gitte. I den inneholdt en ligning allerede bare én variabel, og erstatter verdien av denne med andre ligninger, vi kommer til en løsning. Slik tillegg er en av typene elementær transformasjon av systemet. Ved bruk av Gauss-metoden kan vi bruke flere typer transformasjoner.

Animasjonen ovenfor viser hvordan ligningssystemet gradvis blir til et trapesformet. Det vil si den du så ved den aller første animasjonen og sørget for at det er enkelt å finne verdiene til alle ukjente fra den. Hvordan utføre en slik transformasjon og selvfølgelig eksempler, vil bli diskutert videre.

Når du løser systemer av lineære ligninger med et hvilket som helst antall ligninger og ukjente i ligningssystemet og i den utvidede matrisen til systemet kan:

1. bytte linjer (dette ble nevnt helt i begynnelsen av denne artikkelen);
2. hvis det dukket opp like eller proporsjonale linjer som et resultat av andre transformasjoner, kan de slettes, bortsett fra en;
3. slett "null" rader, der alle koeffisienter er lik null;
4. multiplisere eller dele en streng med et tall;
5. legg til en linje på en linje multiplisert med et tall.

Som et resultat av transformasjonene får vi et system av lineære ligninger tilsvarende den gitte.

Algoritme og eksempler på løsning ved hjelp av Gauss-metoden et system av lineære ligninger med en kvadratisk matrise av systemet

Tenk først på løsningen av systemer med lineære ligninger der antall ukjente er lik antall ligninger. Matrisen til et slikt system er kvadratisk, det vil si at antall rader i det er lik antall kolonner.

Eksempel 2 Løs et system med lineære ligninger ved å bruke Gauss-metoden

Ved å løse systemer av lineære ligninger ved hjelp av skolemetoder multipliserte vi ledd for ledd en av ligningene med et visst tall, slik at koeffisientene til den første variabelen i de to ligningene var motsatte tall. Når man legger til ligninger, elimineres denne variabelen. Gauss-metoden fungerer på lignende måte.

For å forenkle utseende løsninger komponere den utvidede matrisen til systemet:

I denne matrisen er koeffisientene til de ukjente plassert til venstre før den vertikale stolpen, og de frie elementene er til høyre etter den vertikale stolpen.

For enkelhets skyld å dele koeffisientene til variablene (for å få en divisjon med en) bytt den første og andre raden i systemmatrisen. Vi får et system som tilsvarer det gitte, siden man i systemet med lineære ligninger kan omorganisere ligningene:

Med den nye første ligningen eliminere variabelen x fra den andre og alle påfølgende ligninger. For å gjøre dette legger du den første raden multiplisert med (i vårt tilfelle med ) til den andre raden i matrisen, og den første raden multiplisert med (i vårt tilfelle med ) til den tredje raden.

Dette er mulig pga

Hvis det var mer enn tre ligninger i systemet vårt, bør den første linjen legges til alle påfølgende ligninger, multiplisert med forholdet mellom de tilsvarende koeffisientene, tatt med et minustegn.

Som et resultat får vi en matrise som tilsvarer det gitte systemet til et nytt ligningssystem, der alle ligninger, fra den andre inneholder ikke en variabel x :

For å forenkle den andre raden i det resulterende systemet, multipliserer vi den med og får igjen matrisen til ligningssystemet som tilsvarer dette systemet:

Nå, holder den første ligningen til det resulterende systemet uendret, ved å bruke den andre ligningen, eliminerer vi variabelen y fra alle påfølgende ligninger. For å gjøre dette, legg til den andre raden multiplisert med (i vårt tilfelle med ) til den tredje raden i systemmatrisen.

Hvis det var mer enn tre ligninger i systemet vårt, bør den andre linjen legges til alle påfølgende ligninger, multiplisert med forholdet mellom de tilsvarende koeffisientene, tatt med et minustegn.

Som et resultat får vi igjen matrisen til systemet som tilsvarer det gitte systemet med lineære ligninger:

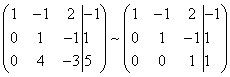
Vi har fått et trapesformet system av lineære ligninger som tilsvarer den gitte:

Hvis antallet ligninger og variabler er større enn i vårt eksempel, fortsetter prosessen med sekvensiell eliminering av variabler til systemmatrisen blir trapesformet, som i vårt demoeksempel.

Vi finner løsningen "fra slutten" - omvendt. For dette fra den siste ligningen vi bestemmer z:
.
Sette denne verdien inn i forrige ligning, finne y:

Fra den første ligningen finne x:

Svar: løsningen av dette ligningssystemet - .

: i dette tilfellet vil det samme svaret bli gitt hvis systemet har en unik løsning. Hvis systemet har et uendelig antall løsninger, vil svaret også gjøre det, og dette er temaet i den femte delen av denne leksjonen.

Løs et system med lineære ligninger ved hjelp av Gauss-metoden selv, og se så på løsningen

Foran oss er igjen et eksempel på et konsistent og bestemt system av lineære ligninger, der antall ligninger er lik antall ukjente. Forskjellen fra vårt demoeksempel fra algoritmen er at det allerede er fire ligninger og fire ukjente.

Eksempel 4 Løs et system med lineære ligninger ved å bruke Gauss-metoden:

Nå må du bruke den andre ligningen for å ekskludere variabelen fra de påfølgende ligningene. La oss bruke forberedende arbeid. For å gjøre det mer praktisk med forholdet mellom koeffisienter, må du få en enhet i den andre kolonnen i den andre raden. For å gjøre dette, trekk den tredje raden fra den andre raden, og multipliser den resulterende andre raden med -1.

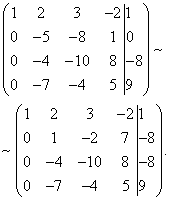
La oss nå utføre den faktiske elimineringen av variabelen fra den tredje og fjerde ligningen. For å gjøre dette legger du den andre, multiplisert med , til den tredje linjen, og den andre, multiplisert med , til den fjerde.

Nå, ved å bruke den tredje ligningen, eliminerer vi variabelen fra den fjerde ligningen. For å gjøre dette, til den fjerde linjen, legg til den tredje, multiplisert med . Vi får en utvidet matrise med en trapesformet form.

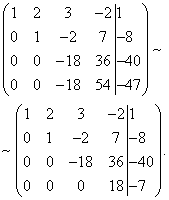
Vi har fått et ligningssystem, som tilsvarer det gitte systemet:

Derfor er de resulterende og gitte systemene konsistente og bestemte. Vi finner den endelige løsningen «fra slutten». Fra den fjerde ligningen kan vi direkte uttrykke verdien av variabelen "x fjerde":

Vi erstatter denne verdien i den tredje ligningen i systemet og får

,

,

Til slutt, verdisubstitusjon

I den første ligningen gir

,

hvor vi finner "x først":

Svar: Dette ligningssystemet har en unik løsning. .

Du kan også sjekke løsningen til systemet på en kalkulator som løser etter Cramers metode: i dette tilfellet vil det samme svaret bli gitt hvis systemet har en unik løsning.

Løsning ved Gauss-metoden for anvendte problemer på eksemplet med et problem for legeringer

Systemer med lineære ligninger brukes til å modellere virkelige objekter i den fysiske verden. La oss løse ett av disse problemene - for legeringer. Lignende oppgaver - oppgaver for blandinger, kostnad eller egenvekt av individuelle varer i en varegruppe og lignende.

Eksempel 5 Tre stykker legering har en totalmasse på 150 kg. Den første legeringen inneholder 60% kobber, den andre - 30%, den tredje - 10%. Samtidig, i den andre og tredje legeringen samlet, er kobber 28,4 kg mindre enn i den første legeringen, og i den tredje legeringen er kobber 6,2 kg mindre enn i den andre. Finn massen til hvert stykke legering.

Løsning. Vi lager et system med lineære ligninger:

Ved å multiplisere den andre og tredje ligningen med 10 får vi et ekvivalent system med lineære ligninger:

Vi komponerer den utvidede matrisen til systemet:

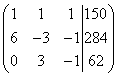
Oppmerksomhet, direkte bevegelse. Ved å legge til (i vårt tilfelle, subtrahere) en rad, multiplisert med et tall (vi bruker det to ganger), skjer følgende transformasjoner med den utvidede matrisen til systemet:

Rettløpet er over. Vi fikk en utvidet matrise med en trapesformet form.

La oss bruke det motsatte. Vi finner en løsning fra slutten. Det ser vi.

Fra den andre ligningen finner vi

Fra den tredje ligningen -

Du kan også sjekke løsningen til systemet på en kalkulator som løser etter Cramers metode: i dette tilfellet vil det samme svaret bli gitt hvis systemet har en unik løsning.

Enkelheten til Gauss-metoden er bevist av det faktum at den tyske matematikeren Carl Friedrich Gauss brukte bare 15 minutter på å finne den opp. I tillegg til metoden for navnet hans, fra Gauss arbeid, er diktet "Vi bør ikke forveksle det som virker utrolig og unaturlig for oss med det absolutt umulige" en slags kort instruksjon for å gjøre funn.

I mange anvendte problemer er det kanskje ikke en tredje begrensning, det vil si en tredje ligning, da er det nødvendig å løse et system med to ligninger med tre ukjente ved hjelp av Gauss-metoden, eller omvendt er det færre ukjente enn ligninger. Vi begynner nå å løse slike ligningssystemer.

Ved å bruke Gauss-metoden kan du finne ut om et system er konsistent eller inkonsekvent n lineære ligninger med n variabler.

Gauss-metode og systemer av lineære ligninger med et uendelig antall løsninger

Følgende eksempel er felles, men ubestemt system lineære ligninger, det vil si å ha et uendelig antall løsninger.

Etter å ha utført transformasjoner i den utvidede matrisen til systemet (permutere rader, multiplisere og dele rader med et visst antall, legge til en rad til en annen), rader av skjemaet

Hvis i alle ligninger har formen

De frie medlemmene er lik null, dette betyr at systemet er ubestemt, det vil si at det har et uendelig antall løsninger, og ligninger av denne typen er "overflødige" og ekskluderes fra systemet.

Eksempel 6

Løsning. La oss komponere den utvidede matrisen til systemet. Deretter, ved å bruke den første ligningen, eliminerer vi variabelen fra de påfølgende ligningene. For å gjøre dette, til den andre, tredje og fjerde linjen, legg til den første, multiplisert med henholdsvis:

La oss nå legge den andre raden til den tredje og fjerde.

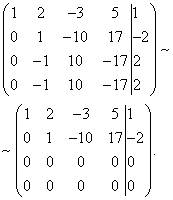
Som et resultat kommer vi til systemet

De to siste likningene har blitt likninger av formen . Disse ligningene er oppfylt for alle verdier av ukjente og kan forkastes.

For å tilfredsstille den andre ligningen, kan vi velge vilkårlige verdier for og , da vil verdien for bli bestemt entydig: . Fra den første ligningen er verdien for også unikt funnet: .

Både de gitte og de siste systemene er kompatible, men ubestemte, og formlene

for vilkårlig og gi oss alle løsninger av det gitte systemet.

Gauss-metoden og systemer av lineære ligninger som ikke har noen løsninger

Følgende eksempel er et inkonsekvent system av lineære ligninger, det vil si at det ikke har noen løsninger. Svaret på slike problemer er formulert som følger: systemet har ingen løsninger.

Som allerede nevnt i forbindelse med det første eksemplet, etter å ha utført transformasjoner i den utvidede matrisen til systemet, linjer i skjemaet

tilsvarende en ligning av formen

Hvis det blant dem er minst én ligning med en fri term som ikke er null (dvs. ), så er dette likningssystemet inkonsekvent, det vil si at det ikke har noen løsninger, og dette fullfører løsningen.

Eksempel 7 Løs systemet med lineære ligninger ved å bruke Gauss-metoden:

Løsning. Vi komponerer den utvidede matrisen til systemet. Ved å bruke den første ligningen ekskluderer vi variabelen fra de påfølgende ligningene. For å gjøre dette, legg til den første multiplisert med til den andre raden, den første multiplisert med den tredje raden, og den første multiplisert med den fjerde raden.

Nå må du bruke den andre ligningen for å ekskludere variabelen fra de påfølgende ligningene. For å oppnå heltallsforhold av koeffisientene, bytter vi andre og tredje rad i den utvidede matrisen til systemet.

For å ekskludere fra den tredje og fjerde ligningen legger du den andre, multiplisert med , til den tredje raden, og den andre, multiplisert med , til den fjerde.

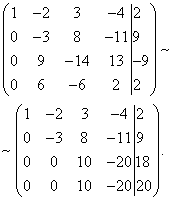
Nå, ved å bruke den tredje ligningen, eliminerer vi variabelen fra den fjerde ligningen. For å gjøre dette, til den fjerde linjen, legg til den tredje, multiplisert med .

Det gitte systemet tilsvarer dermed følgende:

Det resulterende systemet er inkonsekvent, siden dets siste ligning ikke kan tilfredsstilles av noen verdier av de ukjente. Derfor har dette systemet ingen løsninger.

Vi fortsetter å vurdere systemer med lineære ligninger. Denne leksjonen er den tredje om emnet. Hvis du har en vag idé om hva et system med lineære ligninger er generelt, føler du deg som en tekanne, så anbefaler jeg å starte med det grunnleggende på neste side, det er nyttig å studere leksjonen.

Gauss-metoden er enkel! Hvorfor? Den berømte tyske matematikeren Johann Carl Friedrich Gauss fikk i løpet av sin levetid anerkjennelse som den største matematikeren gjennom tidene, et geni og til og med kallenavnet "Kongen av matematikk". Og alt genialt, som du vet, er enkelt! Forresten, ikke bare suckers, men også genier faller inn i pengene - portrettet av Gauss ble flauntet på en seddel på 10 tyske mark (før innføringen av euroen), og Gauss smiler fortsatt mystisk til tyskerne fra vanlige frimerker.

Gauss-metoden er enkel ved at det ER NOK KUNNSKAP TIL EN FEMTE-KLASSE-ELEV til å mestre den. Må kunne addere og multiplisere! Det er ingen tilfeldighet at metoden for suksessiv eliminering av ukjente ofte vurderes av lærere ved skolens matematiske valgfag. Det er et paradoks, men Gauss-metoden forårsaker de største vanskelighetene for elevene. Ikke noe overraskende – alt handler om metodikken, og jeg skal prøve å fortelle i en tilgjengelig form om algoritmen til metoden.

Først systematiserer vi kunnskapen om systemer av lineære ligninger litt. Et system med lineære ligninger kan:

1) Ha en unik løsning. 2) Har uendelig mange løsninger. 3) Har ingen løsninger (vær uforenlig).

Gauss-metoden er det kraftigste og mest allsidige verktøyet for å finne en løsning noen systemer av lineære ligninger. Som vi husker Cramers regel og matrisemetode er uegnet i tilfeller hvor systemet har uendelig mange løsninger eller er inkonsekvent. En metode for suksessiv eliminering av ukjente uansett lede oss til svaret! I denne leksjonen vil vi igjen vurdere Gauss-metoden for sak nr. 1 (den eneste løsningen på systemet), en artikkel er reservert for situasjonene i punkt nr. 2-3. Jeg legger merke til at selve metodealgoritmen fungerer på samme måte i alle tre tilfellene.

La oss gå tilbake til det enkleste systemet fra leksjonen Hvordan løse et system med lineære ligninger? og løse det ved hjelp av Gauss-metoden.

Det første trinnet er å skrive utvidet matrisesystem: . Etter hvilket prinsipp koeffisientene registreres, tror jeg alle kan se. Den vertikale linjen inne i matrisen har ingen matematisk betydning - det er bare en gjennomstreking for enkel design.

Referanse : Jeg anbefaler å huske vilkår lineær algebra. Systemmatrise er en matrise som kun består av koeffisienter for ukjente, i dette eksemplet, matrisen til systemet: . Utvidet systemmatrise er den samme matrisen til systemet pluss en kolonne med gratis medlemmer, i dette tilfellet: . Enhver av matrisene kan ganske enkelt kalles en matrise for korthets skyld.

Etter at den utvidede matrisen til systemet er skrevet, er det nødvendig å utføre noen handlinger med den, som også kalles elementære transformasjoner.

Det er følgende elementære transformasjoner:

1) Strenger matriser kan omorganisere steder. For eksempel, i matrisen under vurdering, kan du trygt omorganisere den første og andre raden:

2) Hvis det er (eller dukket opp) proporsjonale (som et spesialtilfelle - identiske) rader i matrisen, følger det slette fra matrisen, alle disse radene unntatt én. Tenk for eksempel på matrisen . I denne matrisen er de tre siste radene proporsjonale, så det er nok å forlate bare en av dem: .

3) Hvis en null-rad dukket opp i matrisen under transformasjonene, følger den også slette. Jeg vil ikke tegne, selvfølgelig, nulllinjen er linjen der bare nuller.

4) Rekken av matrisen kan være multiplisere (dividere) for et hvilket som helst nummer ikke-null. Tenk for eksempel på matrisen . Her er det tilrådelig å dele den første linjen med -3, og multiplisere den andre linjen med 2: . Denne handlingen er veldig nyttig, siden den forenkler ytterligere transformasjoner av matrisen.

5) Denne transformasjonen forårsaker de fleste vanskelighetene, men faktisk er det heller ikke noe komplisert. Til raden i matrisen kan du legg til en annen streng multiplisert med et tall, forskjellig fra null. Tenk på matrisen vår fra et praktisk eksempel: . Først vil jeg beskrive transformasjonen i detalj. Multipliser den første raden med -2: , og til den andre linjen legger vi den første linjen multiplisert med -2: . Nå kan den første linjen deles "tilbake" med -2: . Som du kan se, er linjen som legges til LI – har ikke endret seg. Er alltid linjen endres, SOM LEGGES TIL UT.

I praksis maler de selvfølgelig ikke så detaljert, men skriver kortere: Nok en gang: til andre linje lagt til den første raden multiplisert med -2. Linjen multipliseres vanligvis muntlig eller på et utkast, mens det mentale forløpet av beregninger er noe sånt som dette:

"Jeg skriver om matrisen og skriver om den første raden: »

Første kolonne først. Nedenfor må jeg få null. Derfor multipliserer jeg enheten ovenfor med -2:, og legger den første til den andre linjen: 2 + (-2) = 0. Jeg skriver resultatet i den andre linjen: »

«Nå den andre kolonnen. Over -1 ganger -2: . Jeg legger den første til den andre linjen: 1 + 2 = 3. Jeg skriver resultatet til den andre linjen: »

«Og den tredje kolonnen. Over -5 ganger -2: . Jeg legger den første linjen til den andre linjen: -7 + 10 = 3. Jeg skriver resultatet i den andre linjen: »

Vennligst tenk nøye over dette eksemplet og forstå sekvensiell beregningsalgoritme, hvis du forstår dette, så er Gauss-metoden praktisk talt "i lommen". Men vi jobber selvfølgelig fortsatt med denne transformasjonen.

Elementære transformasjoner endrer ikke løsningen av ligningssystemet

! MERK FØLGENDE: betraktet som manipulasjoner kan ikke bruke, hvis du får tilbud om en oppgave hvor matrisene er gitt «av seg selv». For eksempel med "klassisk" matriser ikke i noe tilfelle bør du omorganisere noe inne i matrisene! La oss gå tilbake til systemet vårt. Hun er praktisk talt brutt i stykker.

La oss skrive den utvidede matrisen til systemet og ved å bruke elementære transformasjoner redusere den til trinnvis utsikt:

(1) Den første raden ble lagt til den andre raden, multiplisert med -2. Og igjen: hvorfor multipliserer vi den første raden med -2? For å få null nederst, som betyr å bli kvitt en variabel i den andre linjen.

(2) Del den andre raden med 3.

Formålet med elementære transformasjoner – konverter matrisen til trinnform: . I utformingen av oppgaven trekker de direkte ut "stigen" med en enkel blyant, og sirkler også tallene som er plassert på "trinnene". Selve begrepet "trinnsyn" er ikke helt teoretisk; i vitenskapelig og pedagogisk litteratur kalles det ofte trapesformet utsikt eller trekantet utsikt.

Som et resultat av elementære transformasjoner har vi oppnådd tilsvarende opprinnelige ligningssystem:

Nå må systemet "utvinnes" i motsatt retning - fra bunnen og opp kalles denne prosessen omvendt Gauss-metode.

I den nedre ligningen har vi allerede det ferdige resultatet: .

Vurder den første ligningen til systemet og bytt inn den allerede kjente verdien av "y" i den:

La oss vurdere den vanligste situasjonen når Gauss-metoden er nødvendig for å løse et system med tre lineære ligninger med tre ukjente.

Eksempel 1

Løs ligningssystemet ved å bruke Gauss-metoden:

La oss skrive den utvidede matrisen til systemet:

Nå vil jeg umiddelbart tegne resultatet som vi kommer til i løpet av løsningen: Og jeg gjentar, målet vårt er å bringe matrisen til en trinnvis form ved hjelp av elementære transformasjoner. Hvor skal man begynne å ta grep?

Se først på nummeret øverst til venstre: Burde nesten alltid være her enhet. Generelt sett vil -1 (og noen ganger andre tall) også passe, men på en eller annen måte har det tradisjonelt skjedd at en enhet vanligvis plasseres der. Hvordan organisere en enhet? Vi ser på den første kolonnen - vi har en ferdig enhet! Transformasjon én: bytt første og tredje linje:

Nå vil den første linjen forbli uendret til slutten av løsningen. Nå fint.

Enheten øverst til venstre er organisert. Nå må du få nuller på disse stedene:

Nuller oppnås bare ved hjelp av en "vanskelig" transformasjon. Først tar vi for oss den andre linjen (2, -1, 3, 13). Hva må gjøres for å få null i første posisjon? Trenge til den andre linjen legg til den første linjen multiplisert med -2. Mentalt eller på et utkast multipliserer vi den første linjen med -2: (-2, -4, 2, -18). Og vi utfører konsekvent (igjen mentalt eller på et utkast) tillegg, til den andre linjen legger vi til den første linjen, allerede multiplisert med -2:

Resultatet er skrevet i andre linje:

På samme måte tar vi for oss den tredje linjen (3, 2, -5, -1). For å få null i første posisjon, trenger du til den tredje linjen legg til den første linjen multiplisert med -3. Mentalt eller på et utkast multipliserer vi den første linjen med -3: (-3, -6, 3, -27). Og til den tredje linjen legger vi den første linjen multiplisert med -3:

Resultatet er skrevet i tredje linje:

I praksis blir disse handlingene vanligvis utført muntlig og skrevet ned i ett trinn:

Du trenger ikke å telle alt på en gang og samtidig. Rekkefølgen på beregninger og "innsetting" av resultater konsistent og vanligvis slik: først omskriver vi den første linjen, og puster oss stille - KONSEKVENT og NØYE:
Og jeg har allerede vurdert det mentale forløpet til selve beregningene ovenfor.

I dette eksemplet er dette enkelt å gjøre, vi deler den andre linjen med -5 (siden alle tallene der er delbare med 5 uten en rest). Samtidig deler vi den tredje linjen med -2, fordi jo mindre tall, jo enklere er løsningen:

På sluttstadiet av elementære transformasjoner må en mer null oppnås her:

For dette til den tredje linjen legger vi den andre linjen, multiplisert med -2:
Prøv å analysere denne handlingen selv - multipliser den andre linjen mentalt med -2 ​​og utfør addisjonen.

Den siste handlingen som utføres er frisyren til resultatet, del den tredje linjen med 3.

Som et resultat av elementære transformasjoner ble et ekvivalent innledende system av lineære ligninger oppnådd: Kul.

Nå kommer den omvendte kursen til Gauss-metoden inn. Ligningene "slapper av" fra bunnen og opp.

I den tredje ligningen har vi allerede det ferdige resultatet:

La oss se på den andre ligningen: . Betydningen av "z" er allerede kjent, således:

Og til slutt, den første ligningen: . "Y" og "Z" er kjent, saken er liten:

Svar:

Som det har blitt bemerket gjentatte ganger, for ethvert ligningssystem er det mulig og nødvendig å sjekke den funnet løsningen, heldigvis er dette ikke vanskelig og raskt.

Eksempel 2

Dette er et eksempel for selvløsning, et eksempel på etterbehandling og et svar på slutten av leksjonen.

Det skal bemerkes at din handlingsforløp faller kanskje ikke sammen med min handling, og dette er et trekk ved Gauss-metoden. Men svarene må være de samme!

Eksempel 3

Løs et system med lineære ligninger ved å bruke Gauss-metoden

Vi ser på øvre venstre "trinn". Der burde vi ha en enhet. Problemet er at det ikke er noen i den første kolonnen i det hele tatt, så ingenting kan løses ved å omorganisere radene. I slike tilfeller må enheten organiseres ved hjelp av en elementær transformasjon. Dette kan vanligvis gjøres på flere måter. Jeg gjorde dette: (1) Til den første linjen legger vi den andre linjen, multiplisert med -1. Det vil si at vi mentalt multipliserte den andre linjen med -1 og utførte addisjonen av den første og andre linjen, mens den andre linjen ikke endret seg.

Nå øverst til venstre "minus en", som passer oss perfekt. Hvem som ønsker å få +1 kan utføre en ekstra gest: multipliser den første linjen med -1 (endre fortegn).

(2) Den første raden multiplisert med 5 ble lagt til den andre raden. Den første raden multiplisert med 3 ble lagt til den tredje raden.

(3) Den første linjen ble multiplisert med -1, i prinsippet er dette for skjønnhet. Tegnet på den tredje linjen ble også endret og flyttet til andreplassen, og på det andre trinnet hadde vi den ønskede enheten.

(4) Den andre linjen multiplisert med 2 ble lagt til den tredje linjen.

(5) Den tredje raden ble delt med 3.

Et dårlig tegn som indikerer en regnefeil (sjeldnere en skrivefeil) er en "dårlig" bunnlinje. Det vil si, hvis vi fikk noe som nedenfor, og følgelig, , så kan det med høy grad av sannsynlighet hevdes at det ble gjort en feil i løpet av elementære transformasjoner.

Vi belaster det motsatte trekket, i utformingen av eksempler blir selve systemet ofte ikke skrevet om, og ligningene er "tatt direkte fra den gitte matrisen". Det omvendte trekket, minner jeg deg på, fungerer fra bunnen og opp. Ja, her er en gave:

Svar: .

Eksempel 4

Løs et system med lineære ligninger ved å bruke Gauss-metoden

Dette er et eksempel på en uavhengig løsning, det er noe mer komplisert. Det er greit hvis noen blir forvirret. Full løsning og designeksempel på slutten av leksjonen. Din løsning kan avvike fra min.

I den siste delen tar vi for oss noen funksjoner i Gauss-algoritmen. Den første funksjonen er at noen ganger mangler noen variabler i systemets likninger, for eksempel: Hvordan skrive den utvidede matrisen til systemet riktig? Jeg snakket allerede om dette øyeblikket i leksjonen. Cramers regel. Matrisemetode. I den utvidede matrisen til systemet setter vi nuller i stedet for de manglende variablene: Forresten, dette er et ganske enkelt eksempel, siden det allerede er en null i den første kolonnen, og det er færre elementære transformasjoner å utføre.

Den andre funksjonen er denne. I alle eksemplene som ble vurdert, plasserte vi enten -1 eller +1 på "trinnene". Kan det være andre tall? I noen tilfeller kan de. Tenk på systemet: .

Her på øvre venstre "trinn" har vi en toer. Men vi legger merke til det faktum at alle tallene i den første kolonnen er delbare med 2 uten en rest - og ytterligere to og seks. Og toeren øverst til venstre vil passe oss! På det første trinnet må du utføre følgende transformasjoner: legg til den første linjen multiplisert med -1 til den andre linjen; til den tredje linjen legg til den første linjen multiplisert med -3. Dermed vil vi få de ønskede nullene i den første kolonnen.

Eller et annet hypotetisk eksempel: . Her passer også trippelen på det andre "trinnet", siden 12 (stedet der vi må få null) er delelig med 3 uten en rest. Det er nødvendig å utføre følgende transformasjon: til den tredje linjen, legg til den andre linjen, multiplisert med -4, som et resultat av at null vi trenger vil bli oppnådd.

Gauss-metoden er universell, men det er en særegenhet. Du kan trygt lære hvordan du løser systemer med andre metoder (Cramers metode, matrisemetode) bokstavelig talt fra første gang - det er en veldig rigid algoritme. Men for å føle deg trygg på Gauss-metoden, bør du "fylle hånden" og løse minst 5-10 ti systemer. Derfor kan det til å begynne med være forvirring, feil i beregninger, og det er ikke noe uvanlig eller tragisk i dette.

Regnfullt høstvær utenfor vinduet .... Derfor, for alle, et mer komplekst eksempel for en uavhengig løsning:

Eksempel 5

Løs et system med 4 lineære ligninger med fire ukjente ved hjelp av Gauss-metoden.

En slik oppgave i praksis er ikke så sjelden. Jeg tror at selv en tekanne som har studert denne siden i detalj forstår algoritmen for å løse et slikt system intuitivt. I utgangspunktet det samme - bare mer action.

De tilfellene hvor systemet ikke har noen løsninger (inkonsekvente) eller har uendelig mange løsninger vurderes i timen. Inkompatible systemer og systemer med felles løsning. Der kan du fikse den betraktede algoritmen til Gauss-metoden.

Ønsker deg suksess!

Løsninger og svar:

Eksempel 2: Løsning : La oss skrive ned den utvidede matrisen til systemet og, ved hjelp av elementære transformasjoner, bringe den til en trinnvis form.
Utførte elementære transformasjoner: (1) Den første raden ble lagt til den andre raden, multiplisert med -2. Den første linjen ble lagt til den tredje linjen, multiplisert med -1. Merk følgende! Her kan det være fristende å trekke den første fra den tredje linjen, jeg anbefaler på det sterkeste ikke å trekke fra - risikoen for feil øker betraktelig. Vi bare bretter! (2) Tegnet til den andre linjen ble endret (multiplisert med -1). Den andre og tredje linjen er byttet. Merk at vi på "trinnene" ikke bare er fornøyd med en, men også med -1, noe som er enda mer praktisk. (3) Til den tredje linjen legger du til den andre linjen, multiplisert med 5. (4) Tegnet til den andre linjen ble endret (multiplisert med -1). Den tredje linjen ble delt med 14.

Omvendt trekk:

Svar : .

Eksempel 4: Løsning : Vi skriver den utvidede matrisen til systemet og, ved hjelp av elementære transformasjoner, bringer det til en trinnform:

Utførte konverteringer: (1) Den andre linjen ble lagt til den første linjen. Dermed er den ønskede enheten organisert på øvre venstre "trinn". (2) Den første raden multiplisert med 7 ble lagt til den andre raden. Den første raden multiplisert med 6 ble lagt til den tredje raden.

Med det andre "steget" er alt verre , "kandidatene" for det er tallene 17 og 23, og vi trenger enten en eller -1. Transformasjoner (3) og (4) vil være rettet mot å oppnå ønsket enhet (3) Den andre linjen ble lagt til den tredje linjen, multiplisert med -1. (4) Den tredje linjen, multiplisert med -3, ble lagt til den andre linjen. Det nødvendige på det andre trinnet er mottatt . (5) Til den tredje linjen legges den andre, multiplisert med 6. (6) Den andre raden ble multiplisert med -1, den tredje raden ble delt med -83.

Omvendt trekk:

Svar :

Eksempel 5: Løsning : La oss skrive ned matrisen til systemet og, ved hjelp av elementære transformasjoner, bringe den til en trinnvis form:

Utførte konverteringer: (1) Første og andre linje er byttet. (2) Den første raden ble lagt til den andre raden, multiplisert med -2. Den første linjen ble lagt til den tredje linjen, multiplisert med -2. Den første linjen ble lagt til den fjerde linjen, multiplisert med -3. (3) Den andre linjen multiplisert med 4 ble lagt til den tredje linjen. Den andre linjen multiplisert med -1 ble lagt til den fjerde linjen. (4) Tegnet til den andre linjen er endret. Den fjerde linjen ble delt med 3 og plassert i stedet for den tredje linjen. (5) Den tredje linjen ble lagt til den fjerde linjen, multiplisert med -5.

Omvendt trekk:

Svar :

Helt siden begynnelsen av 1500- og 1700-tallet begynte matematikere å intensivt studere funksjonene, takket være at så mye har endret seg i livene våre. Datateknologi uten denne kunnskapen ville rett og slett ikke eksistert. For å løse komplekse problemer, lineære ligninger og funksjoner er det laget ulike konsepter, teoremer og løsningsteknikker. En av slike universelle og rasjonelle metoder og teknikker for å løse lineære ligninger og deres systemer var Gauss-metoden. Matriser, deres rangering, determinant - alt kan beregnes uten å bruke komplekse operasjoner.

Hva er SLAU

I matematikk er det konseptet SLAE - et lineært system algebraiske ligninger. Hva representerer hun? Dette er et sett med m likninger med de nødvendige n ukjente, vanligvis betegnet som x, y, z eller x 1, x 2 ... x n, eller andre symboler. Løs etter Gauss-metoden dette systemet- betyr å finne alle nødvendige ukjente. Hvis systemet har samme nummer ukjente og ligninger, da kalles det et n-te ordenssystem.

De mest populære metodene for å løse SLAE

PÅ utdanningsinstitusjoner videregående opplæring studerer ulike teknikker for å løse slike systemer. Oftest er dette enkle ligninger som består av to ukjente, så alle eksisterende metode det vil ikke ta lang tid å finne svar på dem. Det kan være som en substitusjonsmetode, når en annen ligning er avledet fra en ligning og erstattet med den opprinnelige. Eller ledd for ledd subtraksjon og addisjon. Men Gauss-metoden regnes som den enkleste og mest universelle. Det gjør det mulig å løse ligninger med et hvilket som helst antall ukjente. Hvorfor anses denne teknikken som rasjonell? Alt er enkelt. Matrisemetoden er god fordi den ikke krever flere ganger å omskrive unødvendige tegn i form av ukjente, det er nok å gjøre aritmetiske operasjoner på koeffisientene - og du vil få et pålitelig resultat.

Hvor brukes SLAE-er i praksis?

Løsningen til SLAE er skjæringspunktene for linjer på grafene til funksjoner. I vår høyteknologiske datamaskinalder trenger folk som er tett involvert i utviklingen av spill og andre programmer å vite hvordan de løser slike systemer, hva de representerer og hvordan de kan kontrollere riktigheten av det resulterende resultatet. Oftest utvikler programmerere spesielle lineære algebrakalkulatorer, dette inkluderer et system med lineære ligninger. Gauss-metoden lar deg beregne alle eksisterende løsninger. Andre forenklede formler og teknikker brukes også.

SLAE-kompatibilitetskriterium

Et slikt system kan bare løses hvis det er kompatibelt. For klarhetens skyld presenterer vi SLAE i formen Ax=b. Den har en løsning hvis rang(A) er lik rang(A,b). I dette tilfellet er (A,b) en utvidet formmatrise som kan hentes fra matrise A ved å omskrive den med frie termer. Det viser seg at det er ganske enkelt å løse lineære ligninger ved hjelp av Gauss-metoden.

Kanskje noen notasjon ikke er helt klar, så det er nødvendig å vurdere alt med et eksempel. La oss si at det er et system: x+y=1; 2x-3y=6. Den består av bare to ligninger der det er 2 ukjente. Systemet vil bare ha en løsning hvis rangeringen til matrisen er lik rangeringen til den utvidede matrisen. Hva er en rangering? Dette er antallet uavhengige linjer i systemet. I vårt tilfelle er rangeringen av matrisen 2. Matrise A vil bestå av koeffisientene som ligger nær de ukjente, og koeffisientene bak tegnet "=" vil også passe inn i den utvidede matrisen.

Hvorfor SLAE kan representeres i matriseform

Basert på kompatibilitetskriteriet i henhold til det påviste Kronecker-Capelli-teoremet, kan systemet med lineære algebraiske ligninger representeres i matriseform. Ved å bruke den Gaussiske kaskademetoden kan du løse matrisen og få det eneste pålitelige svaret for hele systemet. Hvis rangeringen til en vanlig matrise er lik rangeringen av dens utvidede matrise, men mindre enn antallet ukjente, har systemet et uendelig antall svar.

Matrisetransformasjoner

Før du går videre til å løse matriser, er det nødvendig å vite hvilke handlinger som kan utføres på elementene deres. Det er flere elementære transformasjoner:

• Ved å omskrive systemet til en matriseform og utføre dets løsning, er det mulig å multiplisere alle elementene i serien med samme koeffisient.
• For å konvertere en matrise til kanonisk form, kan to parallelle rader byttes. Den kanoniske formen innebærer at alle elementene i matrisen som er plassert langs hoveddiagonalen blir enere, og de resterende blir nuller.
• De tilsvarende elementene i de parallelle radene i matrisen kan legges til hverandre.

Jordan-Gauss-metoden

Essensen av å løse systemer med lineære homogene og inhomogene ligninger ved Gauss-metoden er å gradvis eliminere de ukjente. La oss si at vi har et system med to ligninger der det er to ukjente. For å finne dem må du sjekke systemet for kompatibilitet. Gaussligningen er løst veldig enkelt. Det er nødvendig å skrive ut koeffisientene som ligger nær hver ukjent i en matriseform. For å løse systemet må du skrive ut den utvidede matrisen. Hvis en av ligningene inneholder et mindre antall ukjente, må "0" settes i stedet for det manglende elementet. Alle kjente transformasjonsmetoder brukes på matrisen: multiplikasjon, divisjon med et tall, legge til de tilsvarende elementene i radene til hverandre og andre. Det viser seg at i hver rad er det nødvendig å forlate en variabel med verdien "1", resten skal reduseres til null. For en mer nøyaktig forståelse er det nødvendig å vurdere Gauss-metoden med eksempler.

Et enkelt eksempel på løsning av et 2x2-system

Til å begynne med, la oss ta et enkelt system med algebraiske ligninger, der det vil være 2 ukjente.

La oss omskrive det i en utvidet matrise.

For å løse dette systemet med lineære ligninger, kreves det bare to operasjoner. Vi må bringe matrisen til den kanoniske formen slik at det er enheter langs hoveddiagonalen. Så oversetter vi fra matriseformen tilbake til systemet, får vi ligningene: 1x+0y=b1 og 0x+1y=b2, der b1 og b2 er svarene som er oppnådd i prosessen med å løse.

1. Det første trinnet i å løse den utvidede matrisen vil være som følger: den første raden må multipliseres med -7 og de tilsvarende elementene legges til henholdsvis den andre raden for å bli kvitt en ukjent i den andre ligningen.
2. Siden løsningen av ligninger ved Gauss-metoden innebærer å bringe matrisen til den kanoniske formen, er det nødvendig å gjøre de samme operasjonene med den første ligningen og fjerne den andre variabelen. For å gjøre dette trekker vi den andre linjen fra den første og får det nødvendige svaret - løsningen av SLAE. Eller, som vist i figuren, multipliserer vi den andre raden med en faktor på -1 og legger til elementene i den andre raden til den første raden. Dette er det samme.

Som du kan se, er systemet vårt løst etter Jordan-Gauss-metoden. Vi omskriver den i den nødvendige formen: x=-5, y=7.

Et eksempel på løsning av SLAE 3x3

Anta at vi har et mer komplekst system av lineære ligninger. Gauss-metoden gjør det mulig å beregne svaret selv for det mest tilsynelatende forvirrende systemet. Derfor, for å gå dypere inn i beregningsmetodikken, kan vi gå videre til et mer komplekst eksempel med tre ukjente.

Som i forrige eksempel, omskriver vi systemet i form av en utvidet matrise og begynner å bringe det til den kanoniske formen.

For å løse dette systemet, må du utføre mye flere handlinger enn i forrige eksempel.

1. Først må du lage ett enkelt element i den første kolonnen og resten nuller. For å gjøre dette, multipliser den første ligningen med -1 og legg den andre ligningen til den. Det er viktig å huske at vi omskriver den første linjen i sin opprinnelige form, og den andre - allerede i modifisert form.
2. Deretter fjerner vi den samme første ukjente fra den tredje ligningen. For å gjøre dette, multipliserer vi elementene i den første raden med -2 ​​og legger dem til den tredje raden. Nå er den første og andre linjen skrevet om i sin opprinnelige form, og den tredje - allerede med endringer. Som du kan se av resultatet, fikk vi den første i begynnelsen av hoveddiagonalen til matrisen, og resten er null. Noen flere handlinger, og ligningssystemet ved Gauss-metoden vil bli løst pålitelig.
3. Nå må du gjøre operasjoner på andre elementer i radene. Tredje og fjerde trinn kan kombineres til ett. Vi må dele den andre og tredje linjen med -1 for å bli kvitt de negative på diagonalen. Vi har allerede brakt den tredje linjen til ønsket form.
4. Deretter kanoniserer vi den andre linjen. For å gjøre dette multipliserer vi elementene i den tredje raden med -3 og legger dem til den andre linjen i matrisen. Det kan ses av resultatet at den andre linjen også er redusert til den formen vi trenger. Det gjenstår å gjøre noen flere operasjoner og fjerne koeffisientene til de ukjente fra den første raden.
5. For å lage 0 fra det andre elementet i raden, må du multiplisere den tredje raden med -3 og legge den til den første raden.
6. Det neste avgjørende trinnet er å legge til den første linjen nødvendige elementer andre rad. Så vi får den kanoniske formen til matrisen, og følgelig svaret.

Som du kan se, er løsningen av ligninger ved Gauss-metoden ganske enkel.

Et eksempel på løsning av et 4x4 ligningssystem

Noen mer komplekse ligningssystemer kan løses ved hjelp av Gauss-metoden ved hjelp av dataprogrammer. Det er nødvendig å kjøre koeffisienter for ukjente inn i eksisterende tomme celler, og programmet vil beregne det nødvendige resultatet trinn for trinn, og beskrive hver handling i detalj.

Beskrevet nedenfor trinn-for-trinn instruksjon løsninger på dette eksemplet.

I det første trinnet legges frie koeffisienter og tall for ukjente inn i tomme celler. Dermed får vi den samme utvidede matrisen som vi skriver for hånd.

Og alle nødvendige aritmetiske operasjoner utføres for å bringe den utvidede matrisen til den kanoniske formen. Det må forstås at svaret på et ligningssystem ikke alltid er heltall. Noen ganger kan løsningen være fra brøktall.

Kontroller at løsningen er riktig

Jordan-Gauss-metoden sørger for å kontrollere riktigheten av resultatet. For å finne ut om koeffisientene er beregnet riktig, trenger du bare å erstatte resultatet i det opprinnelige ligningssystemet. Venstre side av ligningen må samsvare med høyre side, som er bak likhetstegnet. Hvis svarene ikke stemmer overens, må du beregne systemet på nytt eller prøve å bruke en annen metode for å løse SLAE kjent for deg, for eksempel subtraksjon eller termin-for-term subtraksjon og addisjon. Tross alt er matematikk en vitenskap som har et stort antall forskjellige metoder for å løse. Men husk: resultatet skal alltid være det samme, uansett hvilken løsningsmetode du brukte.

Gauss-metoden: de vanligste feilene ved å løse SLAE

Under avgjørelsen lineære systemer ligninger, feil som feil overføring av koeffisienter til matriseform forekommer oftest. Det er systemer der noen ukjente mangler i en av ligningene, og ved å overføre dataene til den utvidede matrisen kan de gå tapt. Som et resultat, når du løser dette systemet, kan det hende at resultatet ikke samsvarer med det virkelige.

En annen av hovedfeilene kan være feil å skrive ut det endelige resultatet. Det må være klart forstått at den første koeffisienten vil tilsvare den første ukjente fra systemet, den andre - til den andre, og så videre.

Gauss-metoden beskriver i detalj løsningen av lineære ligninger. Takket være ham er det enkelt å utføre de nødvendige operasjonene og finne det riktige resultatet. I tillegg er dette et universelt verktøy for å finne et pålitelig svar på ligninger av enhver kompleksitet. Kanskje det er derfor det brukes så ofte for å løse SLAE.

I dag tar vi for oss Gauss-metoden for å løse systemer av lineære algebraiske ligninger. Du kan lese om hva disse systemene er i den forrige artikkelen viet til å løse den samme SLAE ved Cramer-metoden. Gauss-metoden krever ingen spesifikk kunnskap, kun omsorg og konsistens er nødvendig. Til tross for at fra et matematikksynspunkt er skoleforberedelse nok for anvendelsen, fører det ofte til vanskeligheter for elevene å mestre denne metoden. I denne artikkelen vil vi prøve å redusere dem til ingenting!

Gauss metode

M Gauss metode er den mest universelle metoden for å løse SLAE (med unntak av, vel, veldig store systemer). I motsetning til den som ble diskutert tidligere, passer den ikke bare for systemer som har en unik løsning, men også for systemer som har et uendelig antall løsninger. Det er tre alternativer her.

1. Systemet har en unik løsning (determinanten for hovedmatrisen til systemet er ikke lik null);
2. Systemet har et uendelig antall løsninger;
3. Det finnes ingen løsninger, systemet er inkonsekvent.

Så vi har et system (la det ha én løsning), og vi skal løse det ved å bruke Gauss-metoden. Hvordan det fungerer?

Gaussmetoden består av to stadier - direkte og invers.

Direkte Gauss-metoden

Først skriver vi den utvidede matrisen til systemet. For å gjøre dette legger vi til en kolonne med gratis medlemmer til hovedmatrisen.

Hele essensen av Gauss-metoden er å redusere denne matrisen til en trinnvis (eller, som de sier, trekantet) form ved hjelp av elementære transformasjoner. I denne formen skal det bare være nuller under (eller over) hoveddiagonalen til matrisen.

Hva kan bli gjort:

1. Du kan omorganisere radene i matrisen;
2. Hvis det er identiske (eller proporsjonale) rader i matrisen, kan du slette alle unntatt én av dem;
3. Du kan multiplisere eller dele en streng med et hvilket som helst tall (unntatt null);
4. Null linjer fjernes;
5. Du kan legge til en streng multiplisert med et tall som ikke er null, til en streng.

Omvendt Gauss-metode

Etter at vi har transformert systemet på denne måten, en ukjent xn blir kjent, og det er mulig å finne alle de gjenværende ukjente i omvendt rekkefølge, og erstatte de allerede kjente x-ene i systemets likninger, opp til den første.

Når Internett alltid er tilgjengelig, kan du løse ligningssystemet ved hjelp av Gauss-metoden på nett . Alt du trenger å gjøre er å legge inn oddsen i den elektroniske kalkulatoren. Men du må innrømme, det er mye mer behagelig å innse at eksemplet ikke ble løst av et dataprogram, men av din egen hjerne.

Et eksempel på løsning av et ligningssystem ved hjelp av Gauss-metoden

Og nå - et eksempel, slik at alt blir klart og forståelig. La et system med lineære ligninger gis, og det er nødvendig å løse det ved Gauss-metoden:

Først, la oss skrive den utvidede matrisen:

La oss nå ta en titt på transformasjonene. Husk at vi må oppnå en trekantet form av matrisen. Multipliser den første raden med (3). Multipliser den andre raden med (-1). La oss legge til den andre raden til den første og få:

Multipliser så den tredje raden med (-1). La oss legge til den tredje linjen til den andre:

Multipliser den første raden med (6). Multipliser den andre raden med (13). La oss legge til den andre linjen til den første:

Voila - systemet bringes til riktig form. Det gjenstår å finne de ukjente:

Systemet i dette eksemplet har en unik løsning. Vi vil vurdere løsningen av systemer med et uendelig sett med løsninger i en egen artikkel. Kanskje du til å begynne med ikke vet hvor du skal begynne med matrisetransformasjoner, men etter passende øvelse vil du få tak i det og klikke på Gaussisk SLAE som nøtter. Og hvis du plutselig kommer over en SLAU, som viser seg å være en for tøff nøtt å knekke, ta kontakt med våre forfattere! du kan ved å legge igjen en søknad i korrespondansen. Sammen vil vi løse ethvert problem!

La oss vurdere nøyaktige metoder for å løse systemet; her er dimensjonsmatrisen

En metode for å løse et problem klassifiseres som eksakt hvis den, under forutsetning av at det ikke er noen avrundinger, gir en nøyaktig løsning på problemet etter et begrenset antall aritmetiske og logiske operasjoner. Hvis antallet ikke-null-elementer i matrisen til systemet er i størrelsesorden , så for de fleste av de for tiden brukte eksakte metodene for å løse slike systemer, er det nødvendige antallet operasjoner i størrelsesorden . Derfor, for anvendeligheten av eksakte metoder, er det nødvendig at en slik rekkefølge av antall operasjoner er akseptabel for en gitt datamaskin; andre begrensninger pålegges av volumet og strukturen til datamaskinminnet.

Klausulen om "metoder som er i bruk" har følgende betydning. Det finnes metoder for å løse slike systemer med et lavere antall operasjoner, men de brukes ikke aktivt på grunn av den sterke følsomheten til resultatet for beregningsfeilen.

Den mest kjente av de eksakte metodene for å løse systemer med lineære ligninger er Gauss-elimineringsmetoden. La oss vurdere en av dens mulige implementeringer. Forutsatt at , den første ligningen av systemet

del på koeffisienten , som et resultat får vi ligningen

Så, fra hver av de gjenværende ligningene, trekkes den første ligningen, multiplisert med den riktige koeffisienten. Som et resultat blir disse ligningene transformert til formen

Den første ukjente viste seg å være ekskludert fra alle ligninger bortsett fra den første. Videre, under forutsetningen at , deler vi den andre ligningen med koeffisienten og ekskluderer det ukjente fra alle ligninger, med start fra den andre osv. Som et resultat av suksessiv eliminering av ukjente, transformeres ligningssystemet til et system av ligninger med en trekantet matrise

Settet med beregninger som ble utført, hvor det opprinnelige problemet ble transformert til formen (2), kalles det direkte forløpet til Gauss-metoden.

Fra likningen til system (2) bestemmer vi , fra , osv. opp til . Helheten av slike beregninger kalles det omvendte forløpet til Gauss-metoden.

Det er lett å sjekke at implementeringen av fremføringen av Gauss-metoden krever aritmetiske operasjoner, og den omvendte kjøringen krever aritmetiske operasjoner.

Unntaket oppstår som et resultat av følgende operasjoner: 1) å dele ligningen med , 2) subtrahere ligningen oppnådd etter slik divisjon, multiplisert med , fra ligninger med tall k . Den første operasjonen tilsvarer å multiplisere ligningssystemet til venstre med den diagonale matrisen

den andre operasjonen tilsvarer multiplikasjon til venstre med matrisen

Dermed kan system (2) oppnådd som et resultat av disse transformasjonene skrives som

Produktet av venstre (høyre) trekantet matrise er en venstre (høyre) trekantet matrise, så C er en venstre trekantet matrise. Fra formelen for elementene i den inverse matrisen

det følger at matrisen invers til en venstre (høyre) trekantet en er en venstre (høyre) trekantet. Derfor er matrisen trekantet.

La oss introdusere notasjonen. I følge konstruksjonen er alt og matrisen D rett trekantet. Herfra får vi representasjonen av matrisen A som et produkt av venstre og høyre trekantmatriser:

Likhet, sammen med betingelsen , danner et system av ligninger med hensyn til elementene i de trekantede matrisene B og : . Siden for og for , kan dette systemet skrives som

(3)

eller, som er det samme,

Ved å bruke betingelsen om at alt får vi et system med tilbakefallsrelasjoner for å bestemme elementene og:

Beregninger utføres sekvensielt for sett. Her og nedenfor, i tilfellet når den øvre summeringsgrensen er mindre enn den nedre, antas det at hele summen er lik null.

I stedet for suksessive transformasjoner av systemet (1) til formen (2), kan man altså direkte beregne matrisene B og bruke formler (4). Disse beregningene kan bare utføres hvis alle elementene er forskjellige fra null. La være matriser av hovedminorer av rekkefølgen av matrisene A, B, D. I henhold til (3) . Fordi da. Følgelig

Så, for å utføre beregninger i henhold til formlene (4), er det nødvendig og tilstrekkelig å oppfylle betingelsene

I noen tilfeller er det kjent på forhånd at betingelse (5) er oppfylt. For eksempel er mange problemer innen matematisk fysikk redusert til å løse systemer med en positiv bestemt matrise A. Men i generell sak dette kan ikke sies på forhånd. Et slikt tilfelle er også mulig: alt, men blant mengdene er det veldig små, og når de er delt på dem, vil store tall med store absolutte feil bli oppnådd. Som et resultat vil løsningen bli sterkt forvrengt.

La oss betegne . Siden og , så holder likestillingene. Etter å ha dekomponert matrisen til det opprinnelige systemet til produktet av venstre og høyre trekantede matriser, reduseres løsningen av det opprinnelige systemet til den sekvensielle løsningen av to systemer med trekantede matriser; dette vil kreve aritmetiske operasjoner.

Det er ofte praktisk å kombinere sekvensen av operasjoner for å dekomponere matrisen A til produktet av trekantede matriser og for å bestemme vektoren d. Ligninger

systemer kan skrives som

Derfor kan verdiene beregnes samtidig med resten av verdiene ved å bruke formler (4).

Ved løsning av praktiske problemer blir det ofte nødvendig å løse likningssystemer med en matrise som inneholder et stort antall nullelementer.

Vanligvis har disse matrisene en såkalt båndstruktur. Mer presist kalles matrisen A -diagonal eller har en båndstruktur, hvis den er ved . Tallet kalles båndets bredde. Det viser seg at når man løser et ligningssystem med en båndmatrise ved Gauss-metoden, kan antall aritmetiske operasjoner og den nødvendige mengden dataminne reduseres betydelig.

Oppgave 1. Undersøk egenskapene til Gauss-metoden og metoden for å løse systemet ved å bruke dekomponering av båndmatrisen A til produktet av venstre og høyre trekantmatrise. Vis at det kreves aritmetiske operasjoner for å finne løsningen (for ). Finn det ledende medlemmet av antall operasjoner under betingelsen.

Oppgave 2. Estimer mengden lastet datamaskinminne i Gauss-metoden for båndmatriser.

Når man regner uten hjelp av en datamaskin, er det stor sannsynlighet tilfeldige feil. For å eliminere slike feil introduseres noen ganger et kontrollsystem som består av kontrollelementer i systemets ligninger

Ved transformering av ligninger utføres de samme operasjonene på kontrollelementene som på de frie medlemmene av ligningene. Som et resultat må kontrollelementet til hver nye ligning være lik summen av koeffisientene til denne ligningen. Et stort avvik mellom dem indikerer feil i beregningene eller ustabiliteten til beregningsalgoritmen i forhold til beregningsfeilen.

For eksempel, i tilfellet å bringe likningssystemet til form ved bruk av formler (4), beregnes kontrollelementet til hver av likningene i systemet ved å bruke de samme formlene (4). Etter å ha beregnet alle elementene ved en fast kontroll utføres ved å kontrollere likheten

Det omvendte forløpet til Gauss-metoden er også ledsaget av beregningen av kontrollelementene til systemradene.

For å unngå den katastrofale påvirkningen av beregningsfeilen, brukes Gauss-metoden med valg av hovedelementet.

Forskjellen fra skjemaet til den Gaussiske metoden beskrevet ovenfor er som følger. La, i løpet av å eliminere de ukjente, likningssystemet

La oss finne slikt at og ombetegne og ; da vil vi eliminere det ukjente fra alle ligninger, og starter med . En slik redesignering fører til en endring i rekkefølgen for eliminering av ukjente og reduserer i mange tilfeller vesentlig løsningens følsomhet for avrundingsfeil i beregninger.

Ofte er det nødvendig å løse flere ligningssystemer , med samme matrise A. Det er praktisk å gå frem som følger: ved å introdusere notasjonen

La oss utføre beregninger ved å bruke formler (4), og regne ut elementene ved . Som et resultat vil p-likningssystemer med en trekantet matrise oppnås, tilsvarende det opprinnelige problemet

Vi løser disse systemene hver for seg. Det viser seg at det totale antallet aritmetiske operasjoner ved å løse p ligningssystemer på denne måten er .

Teknikken beskrevet ovenfor brukes noen ganger for å få en vurdering av feilen i løsningen, som er en konsekvens av avrundingsfeil i beregninger, uten vesentlige merkostnader. De er gitt av vektoren z med komponenter som om mulig har samme rekkefølge og fortegn som komponentene i den ønskede løsningen; ofte på grunn av mangel på tilstrekkelig informasjon de tar. Vektoren beregnes, og sammen med det opprinnelige ligningssystemet løses systemet.

La og z være faktisk oppnådd løsninger av disse systemene. Bedømmelse av feilen til den ønskede løsningen kan oppnås basert på hypotesen: de relative feilene ved å løse ved eliminasjonsmetoden for systemer med samme matrise og forskjellige høyresider, som er henholdsvis verdiene og , forskjellige ikke et veldig stort antall ganger.

En annen teknikk for å få en vurdering om den reelle verdien av feilen som oppstår ved avrunding i beregninger er å endre skalaen, som endrer bildet av akkumuleringen av beregningsfeilen.

Sammen med det originale systemet løses systemet med samme metode

For og , som ikke er heltallskrefter av to, sammenligningen av vektorene og gir en ide om størrelsen på beregningsfeilen. For eksempel kan du ta .

Studiet av mange problemer fører til behovet for å løse systemer av lineære ligninger med en symmetrisk positiv bestemt matrise. Slike systemer oppstår for eksempel ved løsning differensiallikninger endelige elementmetode eller endelige forskjellsmetoder. I disse tilfellene har systemets matrise også en båndstruktur.

Metoden kvadratrot(Cholesky-metoden). Matrise A er representert som

hvor S er en rettvinklet trekantet matrise, er dens konjugat, dvs.

hvor alle er en diagonal matrise med elementer lik eller -1. Matriselikhet (6) danner et system av ligninger

Lignende ligninger for forkastes, siden ligningene som tilsvarer parene og er ekvivalente. Herfra får vi tilbakevendende formler for å bestemme elementene og:

Matrisen S er rett triangulær, og dermed, etter å ha oppnådd representasjon (6), reduseres løsningen til det opprinnelige systemet også til sekvensiell løsning av to systemer med trekantede matriser. Merk at i tilfellet med alle og .

Oppgave 3. Estimer antall aritmetiske operasjoner og datamaskinens minnebelastning (forutsatt at mengden minne som kreves for å lagre matrisen A reduseres) når du løser et system med en reell positiv bestemt matrise A ved hjelp av kvadratrotmetoden.

Mange programvarepakker for å løse grenseverdiproblemer i matematisk fysikk ved hjelp av endelige elementmetoden er organisert i henhold til følgende skjema. Etter at matrisen til system A er dannet ved å omorganisere rader og kolonner (både rader og kolonner omorganiseres samtidig), konverteres systemet til formen med den minste tapebredden. Deretter brukes kvadratrotmetoden. Samtidig, for å redusere mengden beregninger ved løsning av et system med andre høyresider, lagres matrisen S.