Modeller beskrevet av systemer av to autonome differensiallikninger.

faseplan. Faseportrett. isoklin metode. hovedisokliner. Stabilitet i stabil tilstand. Lineære systemer. Hovedpunkttyper: node, sal, fokus, senter. Eksempel: kjemiske reaksjoner første orden.

De mest interessante resultatene på kvalitativ modellering av egenskapene til biologiske systemer ble oppnådd på modeller av to differensialligninger, som tillater en kvalitativ studie ved hjelp av metoden faseplan. Tenk på et system med to autonome ordinære differensialligninger av den generelle formen

(4.1)

P(x,y), Q(x,y)- kontinuerlige funksjoner definert i noen domene G Euklidisk fly ( x,y- Kartesiske koordinater) og har i dette området kontinuerlige derivater av orden ikke lavere enn den første.

Region G kan enten være ubegrenset eller begrenset. Hvis variabler x, y har en spesifikk biologisk betydning (konsentrasjoner av stoffer, overflod av arter), oftest området G er den positive kvadranten til høyre halvplan:

0 £ x< ¥ ,0 £ y< ¥ .

Konsentrasjonene av stoffer eller mengden av arter kan også begrenses ovenfra av volumet til fartøyet eller av habitatområdet. Deretter har utvalget av variabler formen:

0 £ x< x 0 , 0 £ y< y 0 .

Variabler x, y endring i tid i samsvar med ligningssystemet (4.1), slik at hver tilstand av systemet tilsvarer et par verdier av variabler ( x, y).

Omvendt, for hvert par av variabler ( x, y) tilsvarer en viss tilstand av systemet.

Tenk på et plan med koordinatakser der verdiene til variabler er plottet x,y. Hvert punkt M dette planet tilsvarer en viss tilstand av systemet. Et slikt plan kalles faseplanet og viser helheten av alle tilstander i systemet. Punktet M(x, y) kalles det avbildende eller representerende punktet.

La på første gang t=t 0 som representerer punktkoordinater M 0 (x(t 0),y(t 0)). Ved hvert neste øyeblikk i tid t visningspunktet vil bevege seg i henhold til endringer i verdiene til variablene x(t),y(t). Sett med poeng M(x(t), y(t)) på faseplanet, hvis posisjon tilsvarer tilstandene til systemet i ferd med å endre variabler over tid x(t), y(t) ifølge ligning (4.1), kalles fasebane.

Settet med fasebaner for forskjellige startverdier av variablene gir et lett synlig "portrett" av systemet. Bygning faseportrett lar deg trekke konklusjoner om arten av endringer i variabler x, y uten å kjenne de analytiske løsningene til det opprinnelige ligningssystemet(4.1).

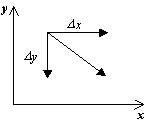
For å skildre et faseportrett, er det nødvendig å konstruere et vektorfelt med retninger for systembanene ved hvert punkt i faseplanet. Ved å spesifisere en økningD t>0,vi får de tilsvarende økningene D x og D y fra uttrykk:

D x=P(x,y)D t,

D y=Q(x,y)D t.

vektor retning dy/dx på punktet ( x, y) avhenger av tegnet til funksjonene P(x, y), Q(x, y) og kan gis av en tabell:

P(x,y)>0,Q(x,y)>0
P(x,y)<0,Q(x,y)<0
P(x,y)>0,Q(x,y)<0
P(x,y)<0,Q(x,y)>0

.(4.2)

Løsning på denne ligningen y=y(x, c), eller implisitt F(x,y)=c, hvor Med er integrasjonskonstanten, gir familien av integralkurver av ligning (4.2) - fasebaner system (4.1) på flyet x, y.

Isoklin metode

For å konstruere et faseportrett bruker man isoklin metode - linjer tegnes på faseplanet som skjærer integralkurvene i en bestemt vinkel. Den isokline ligningen er lett å få fra (4.2). La oss sette

hvor MEN– en viss konstant. Betydning MEN representerer tangenten til hellingen av tangenten til fasebanen og kan ta verdier fra -¥ til + ¥ . Erstatter i stedet for dy/dx i (4.2) mengden MEN vi får den isokline ligningen:

.(4.3)

Ligning (4.3) bestemmer ved hvert punkt i planet den eneste tangenten til den tilsvarende integralkurven, bortsett fra punktet hvor P(x,y)= 0, Q (x,y) = 0 , der retningen til tangenten blir ubestemt, siden verdien av den deriverte blir ubestemt:

.

Dette punktet er skjæringspunktet for alle isokliner - spesielt poeng. Den forsvinner samtidig tidsderivatene til variablene x og y.

Således, ved entallspunktet, er endringshastighetene for variabler lik null. Derfor tilsvarer entallspunktet til differensialligningene til fasebaner (4.2) til stasjonær tilstand av systemet(4.1), og dens koordinater er de stasjonære verdiene til variablene x, y.

Av spesiell interesse er hovedisokliner:

dy/dx=0, P(x,y)=0 – isoklin av horisontale tangenter og

dy/dx=¥ , Q(x,y)=0 – isoklin av vertikale tangenter.

Ved å konstruere hovedisoklinene og finne skjæringspunktet (x,y), hvis koordinater tilfredsstiller vilkårene:

vi vil dermed finne skjæringspunktet for alle isokliner i faseplanet, hvor retningen til tangentene til fasebanene er ubestemt. det - enkeltpunkt, som tilsvarer stasjonær tilstand av systemet(Fig. 4.2).

System (4.1) har like mange stasjonære tilstander som det er skjæringspunkter for hovedisoklinene på faseplanet.

Hver fasebane tilsvarer et sett med bevegelser til et dynamisk system som går gjennom de samme tilstandene og skiller seg fra hverandre bare ved begynnelsen av tidsreferansen.

Hvis betingelsene for Cauchy-teoremet er oppfylt, så gjennom hvert punkt i rommet x, y, t går gjennom en enkelt integrert kurve. Det samme gjelder, takket være autonomi, for fasebaner: en unik fasebane går gjennom hvert punkt i faseplanet.

Stabilitet i stabil tilstand

La systemet være i likevekt.

Deretter er det representative punktet plassert på et av de entallspunktene i systemet, der, per definisjon:

.

Hvorvidt et entallspunkt er stabilt eller ikke avgjøres av om det representative punktet forlater eller ikke med et lite avvik fra den stasjonære tilstanden. Som brukt på et system med to ligninger, definisjonen av stabilitet i språkete, dfølgende.

Likevektstilstanden er stabil hvis for et gitt område med avvik fra likevektstilstanden (e )område kan spesifiseres d (e ), som omgir tilstanden av likevekt og har egenskapen at ingen bane som starter inne i regionen d , vil aldri nå grensen e . (Fig. 4.4)

For en stor klasse systemer - røffe systemer – arten av oppførselen som ikke endres med en liten endring i typen ligninger, informasjon om typen oppførsel i nærheten av den stasjonære tilstanden kan fås ved å studere ikke originalen, men den forenklede linearisert system.

Lineære systemer.

Tenk på et system med to lineære ligninger:

.(4.4)

Her a, b, c, d- konstanter, x, y- Kartesiske koordinater på faseplanet.

Den generelle løsningen vil bli søkt i formen:

.(4.5)

Erstatt disse uttrykkene i (4.4) og reduser med e l t:

(4.6)

Algebraisk ligningssystem (4.6) med ukjente A, B har en løsning som ikke er null bare hvis determinanten, sammensatt av koeffisientene til de ukjente, er lik null:

.

Ved å utvide denne determinanten får vi den karakteristiske ligningen til systemet:

.(4.7)

Løsningen av denne ligningen gir verdiene til indikatorenl 1,2 , under hvilke verdier som ikke er null er mulig for EN og B løsninger av ligning (4.6). Disse verdiene er

.(4.8)

Hvis det radikale uttrykket er negativt, dal 1,2 komplekse konjugerte tall. Anta at begge røttene til ligningen (4.7) har reelle deler som ikke er null og at det ikke er flere røtter. Da kan den generelle løsningen av system (4.4) representeres som en lineær kombinasjon av eksponenter med eksponenterl 1 , l 2 :

(4.9)

For å analysere arten av de mulige banene til systemet på faseplanet bruker vi lineær homogen koordinattransformasjon, som vil bringe systemet til kanonisk form:

,(4.10)

som tillater en mer praktisk representasjon på faseplanet sammenlignet med det opprinnelige systemet (4.4). La oss introdusere nye koordinaterξ , η i henhold til formlene:

(4.1)

Det er kjent fra løpet av lineær algebra at hvis de reelle delene ikke er lik nulll 1 , l 2 det opprinnelige systemet (4.4) ved hjelp av transformasjoner (4.11) kan alltid transformeres til den kanoniske formen (4.10) og dets oppførsel på faseplanet kan studeresξ , η . Vurder de ulike sakene som kan dukke opp her.

Røtter λ 1 , λ 2 – gyldig og av samme tegn

I dette tilfellet er transformasjonskoeffisientene reelle, vi beveger oss fra det virkelige planetx,ytil det virkelige planet ξ, η. Ved å dele den andre av ligningene (4.10) med den første, får vi:

.(4.12)

Ved å integrere denne ligningen finner vi:

Hvor .(4.13)

La oss bli enige om å forstå med λ 2 roten til den karakteristiske ligningen med stor modul, som ikke bryter med allmennheten i resonnementet vårt. Da, siden i tilfellet under vurdering røttene λ 1 , λ2 – gyldig og av samme tegn,en>1 , og vi har å gjøre med integralkurver av parabolsk type.

Alle integralkurver (bortsett fra aksen η , som tilsvarer ) berør ved aksens origo ξ, som også er en integralkurve av ligning (4.11). Opprinnelsen til koordinatene er et enkeltpunkt.

La oss nå finne ut bevegelsesretningen til det representative punktet langs fasebanene. Hvis λ 1, λ 2 er negative, som det fremgår av ligningene (4.10), |ξ|, |η| avta over tid. Det representerende punktet nærmer seg opphavet, men når det aldri. Ellers vil dette være i strid med Cauchys teorem, som sier at bare én fasebane går gjennom hvert punkt i faseplanet.

Et så enkelt punkt som integralkurver passerer, akkurat som en familie av parabler går gjennom origo, kalles en node (fig. 4.5)

Knot-type likevektstilstand ved λ 1, λ 2 < 0 er stabil ifølge Lyapunov, siden det representerende punktet beveger seg langs alle integralkurver mot koordinatenes opprinnelse. den stabil knute. Hvis λ 1, λ 2 > 0, da |ξ|, |η| øke med tiden og det representative punktet beveger seg bort fra origo. I dette tilfellet entallspunktet– ustabil knute .

På faseplanet x, y den generelle kvalitative karakteren av oppførselen til integralkurvene vil forbli, men tangentene til integralkurvene vil ikke falle sammen med koordinataksene. Hellingsvinkelen til disse tangentene vil bli bestemt av forholdet mellom koeffisientene α , β , γ , δ i ligninger (4.11).

Røtter λ 1 , λ 2 er gyldige og har forskjellige tegn.

Konverter fra koordinater x,y til koordinater ξ, η igjen ekte. Ligningene for de kanoniske variablene har igjen formen (4.10), men nå tegnene λ 1, λ 2 forskjellig. Fasebaneligningen har formen:

Hvor , (4.14)

Integrering (4.14), finner vi

(4.15)

den ligningen definerer en familie av kurver av hyperbolsk type, hvor begge koordinatakser er asymptotene (kl en=1 vi ville ha en familie av likebenede hyperbler). Koordinataksene er også integrerte kurver i dette tilfellet– disse vil være de eneste integrerte kurvene som går gjennom origo. Hversom består av trefasebaner: av to bevegelser mot en tilstand av likevekt (eller bort fra en tilstand av likevekt) og fra en tilstand av likevekt. Alle andre integralkurver– er hyperbler som ikke passerer gjennom origo (fig. 4.6) Dette entallspunktet kalles "sal ». Nivålinjene nær fjellsadlen oppfører seg som fasebaner i nærheten av salen.

La oss vurdere arten av bevegelsen til det representative punktet langs fasebaner nær likevektstilstanden. La f.eks.λ 1 > 0 , λ 2<0 . Deretter det representative punktet plassert på aksen ξ , vil bevege seg bort fra origo, og plasseres på aksen η – vil på ubestemt tid nærme seg opprinnelsen til koordinatene, uten å nå det på begrenset tid. Uansett hvor det representerende punktet er i det første øyeblikket (med unntak av entallspunktet og punkter på asymptoten η =0), den vil til slutt bevege seg bort fra likevektstilstanden, selv om den i begynnelsen beveger seg langs en av integralkurvene mot et enkeltpunkt.

Det er åpenbart det sadel-type singular punkt er alltid ustabil . Kun under spesielt valgte startbetingelser på asymptotenη =0 systemet vil nærme seg en tilstand av likevekt. Dette motsier imidlertid ikke påstanden om at systemet er ustabilt. Hvis du teller, at alle starttilstander i systemet på faseplanet er like sannsynlige, da er sannsynligheten for en slik starttilstand som tilsvarer bevegelse i retningen til entallspunkt er lik null. Derfor vil enhver reell bevegelse fjerne systemet fra likevektstilstanden.Går tilbake til koordinatenex,y,vi får det samme kvalitative bildet av arten av bevegelsen av baner rundt opprinnelsen.

Grensen mellom de vurderte tilfellene av en node og en sal er tilfellet når en av de karakteristiske indikatorene, for eksempel λ 1 , forsvinner, som oppstår når determinanten for systemet- uttrykk adbc=0(se formel 4.8 ). I dette tilfellet er koeffisientene til høyresiden av ligningene (4.4) proporsjonale med hverandre:

og systemet har for sine likevektstilstander alle punktene på linjen:

De resterende integrerte kurvene er en familie av parallelle linjer med en helning , langs hvilke de representative punktene enten nærmer seg likevektstilstanden eller beveger seg bort fra den, avhengig av tegnet til den andre roten av den karakteristiske ligningen λ 2 = a+d.(Fig.4.7 ) I dette tilfellet avhenger koordinatene til likevektstilstanden av startverdien til variablene.

Røtter λ 1 , λ 2 – komplekskonjugerer

I dette tilfellet, på ektex og y vi vil har komplekse konjugater ξ , η (4.10) . Men ved å innføre en mellomliggende transformasjon til, er det også i dette tilfellet mulig å redusere hensynet til en reell lineær homogen transformasjon. La oss sette:

(4.16)

hvor a, b, og u, v – reelle verdier. Det kan vises at transformasjonen frax,y til u, v er, under våre forutsetninger, reell, lineær, homogen med en ikke-null determinant. På grunn av ligningene(4.10, 4.16) vi har:

hvor

(4.17)

Dele den andre av ligningene med den første, vi får:

som er lettere å integrere, hvis vi bytter til det polare koordinatsystemet (r, φ ) . Etter bytte vi får fra hvor:

.(4.18)

Altså på faseplanetu, vvi har å gjøre med en familie av logaritmiske spiraler, som hver harasymptotisk punkt ved opprinnelsen.Enkeltpunkt som er det asymptotiske punktet for alle integrerte kurver i form av spiraler, nestet venn ivenn, ringte fokus ( fig.4.8 ) .

La oss vurdere arten av bevegelsen til det representerende punktet langs fasebanene. Multipliser den første av ligningene (4.17) medu, og den andre til v og legger til får vi:

Hvor

La en 1 < 0 (en 1 = Reλ ) . Det representerende punktet nærmer seg deretter origo kontinuerlig uten å nå det på en begrenset tid. Dette betyr at fasebanene er vridningsspiraler og tilsvarer dempede svingninger variabler. det - jevn fokus .

I tilfelle av et stabilt fokus, som i tilfellet med en stabil node, er ikke bare Lyapunov-betingelsen tilfredsstilt, men også et strengere krav. Nemlig for eventuelle innledende avvik vil systemet til slutt returnere så nært likevektsposisjonen som ønsket. Slik stabilitet, der de innledende avvikene ikke bare øker, men forfaller, som tenderer til null, kalles absolutt stabilitet .

Hvis i formelen (4.18) en 1 >0 , så beveger det representerende punktet seg bort fra origo, og vi har å gjøre med ustabilt fokus . Når du flytter fra et flyu, vtil faseplanetx, yspiraler vil også forbli spiraler, men vil bli deformert.

Vurder nå tilfellet nåren 1 =0 . Fasebaner på flyetu, vdet vil være sirkler som på flyetx,ypasse ellipser:

Dermed klen 1=0 gjennom et spesielt punktx= 0,y= 0 ingen integralkurve passerer. Et slikt isolert entallspunkt, i nærheten av hvilket integralkurvene er lukkede kurver, spesielt ellipser innebygd i hverandre og omslutter entallspunktet, kalles et senter.

Dermed er seks typer likevekt mulig, avhengig av arten av røttene til den karakteristiske ligningen (4.7). Utsikt over fasebaner på flyet x, y for disse seks tilfellene er vist i fig. 4.9.

Ris. 4.9.Typer faseportretter i nærheten av en stasjonær tilstand for systemet med lineære ligninger (4.4).

De fem typene likevektstilstander er grove, deres natur endres ikke med tilstrekkelig små endringer på høyresiden av ligninger (4.4). I dette tilfellet bør endringene være små, ikke bare på høyresiden, men også i deres førsteordens derivater. Den sjette likevektstilstanden - sentrum - er ikke grov. Med små endringer i parametrene til høyre side av ligningene, går det inn i et stabilt eller ustabilt fokus.

Bifurkasjonsdiagram

La oss introdusere notasjonen:

. (4.11)

Deretter kan den karakteristiske ligningen skrives på formen:

. (4.12)

Tenk på et plan med rektangulære kartesiske koordinater s , D og merk på den områdene som tilsvarer en eller annen type likevektstilstand, som bestemmes av naturen til røttene til den karakteristiske ligningen

.(4.13)

Betingelsen for stabiliteten til likevektstilstanden vil være tilstedeværelsen av en negativ reell del av yl 1 og l 2 . En nødvendig og tilstrekkelig betingelse for dette er oppfyllelse av ulikhetenes > 0, D > 0 . På diagrammet (4.15) tilsvarer denne tilstanden punktene som ligger i første kvartal av parameterplanet. Entallspunktet vil være fokus hvisl 1 og l 2 kompleks. Denne tilstanden tilsvarer de punktene på flyet som , de. punkter mellom to grener av en parabels 2 = 4 D. Halvaksepunkter s = 0, D>0, tilsvarer likevektstilstander av sentertypen. Like måte,l 1 og l 2 - gyldige, men forskjellige tegn, dvs. et entallspunkt vil være en sal hvis D<0, etc. Som et resultat får vi et partisjonsdiagram av parameterplanet s, D, inn i regioner som tilsvarer forskjellige typer likevektstilstander.

Ris. 4.10. Bifurkasjonsdiagram

for systemet med lineære ligninger 4.4

Hvis koeffisientene til det lineære systemet a, b, c, d avhenger av en parameter, så når denne parameteren endres, vil verdiene også endress , D . Når man passerer gjennom grensene, endres karakteren av faseportrettet kvalitativt. Derfor kalles slike grenser bifurkasjonsgrenser - på motsatte sider av grensen har systemet to topologisk forskjellige faseportretter og følgelig to forskjellige typer atferd.

Diagrammet viser hvordan slike endringer kan skje. Hvis vi ekskluderer spesielle tilfeller - opprinnelsen til koordinatene - så er det lett å se at salen kan gå inn i en node, stabil eller ustabil når den krysser y-aksen. En stabil node kan enten flytte til en sal eller et stabilt fokus, og så videre. Legg merke til at overgangene mellom stabil node-stabilt fokus og ustabil node-ustabil fokusoverganger ikke er bifurkasjonelle, siden topologien til faserommet ikke endres i dette tilfellet. Vi vil snakke mer detaljert om topologien til faserommet og bifurkasjonsovergangene i forelesning 6.

Under bifurkasjonsoverganger endres arten av stabiliteten til singularpunktet. For eksempel kan et stabilt fokus gjennom midten bli til et ustabilt fokus. Denne bifurkasjonen kalles Andronov-Hopf bifurkasjon etter navnene på forskerne som studerte det. Med denne bifurkasjonen i ikke-lineære systemer blir det født en grensesyklus, og systemet blir selvoscillerende (se forelesning 8).

Eksempel. System av lineære kjemiske reaksjoner

Substans X strømmer inn fra utsiden med konstant hastighet, blir til stoff Y og med en hastighet proporsjonal med konsentrasjonen av stoffet Y, tas ut av reaksjonssfæren. Alle reaksjoner er av første orden, med unntak av tilstrømningen av materie fra utsiden, som har null orden. Reaksjonsskjemaet ser slik ut:

(4.14)

og er beskrevet av ligningssystemet:

(4.15)

Vi får stasjonære konsentrasjoner ved å likestille høyresidene til null:

.(4.16)

Vurder faseportrettet av systemet. La oss dele den andre systemligningen (4.16) med den første. Vi får:

.(4.17)

Ligning (4.17) bestemmer oppførselen til variabler på faseplanet. La oss konstruere et faseportrett av dette systemet. Først tegner vi hovedisoklinene på faseplanet. Ligning av isoklinen til vertikale tangenter:

Ligning for isoklinen til horisontale tangenter:

Singularpunktet (stasjonær tilstand) ligger i skjæringspunktet mellom de viktigste isoklinene.

La oss nå bestemme i hvilken vinkel koordinataksene skjærer integralkurvene.

Hvis en x= 0, da.

Dermed er tangenten til hellingen til tangenten til integralkurvene y=y(x), krysser y-aksen x=0, er negativ i det øvre halvplanet (husk at variablene x, y har konsentrasjonsverdier, og derfor er vi kun interessert i øvre høyre kvadrant av faseplanet). I dette tilfellet øker verdien av tangenten til hellingsvinkelen til tangenten med avstanden fra origo.

Tenk på aksen y= 0. I skjæringspunktet mellom denne aksen er integralkurvene beskrevet av ligningen

På tangenten til helningen til integralkurvene som krysser abscisseaksen er positiv og øker fra null til uendelig med økende x.

kl.

Deretter, med en ytterligere økning, synker tangens av skråningen i absolutt verdi, forblir negativ og har en tendens til -1 ved x ® ¥ . Når du kjenner retningen til tangentene til integralkurvene på hovedisolinene og på koordinataksene, er det enkelt å konstruere hele bildet av fasebaner.

Arten av stabiliteten til entallspunktet vil bli etablert ved hjelp av Lyapunov-metoden. Den karakteristiske determinanten til systemet har formen:

.

Ved å utvide determinanten får vi den karakteristiske ligningen til systemet: , dvs. røttene til den karakteristiske ligningen er begge negative. Derfor er den stasjonære tilstanden til systemet en stabil node. Samtidig er konsentrasjonen av stoffet X tenderer til en stasjonær tilstand alltid monotont, konsentrasjonen av stoffet Y kan passere gjennom min eller maks. Oscillerende regimer i et slikt system er umulige.

La zq - entallspunkt for funksjonen f(z), t.s. f(z) men er analytisk på dette punktet (spesielt er det kanskje ikke definert på det). Hvis det eksisterer et slikt punktert nabolag av punktet zq (dvs. settet O z - zq f(z) er aliatisk, da zo kalt isolert entallspunkt funksjoner f(z). Denne definisjonen er også bevart i saken zn = oo, hvis jod er et punktert område av et punkt zq = oo forstår settet z > Jeg - utseendet til en sirkel sentrert ved opprinnelsen. Med andre ord, entallspunktet zq sies å være isolert hvis det finnes et nabolag til dette punktet der det er andre entallspunkter som er forskjellige fra zq. Overalt nedenfor vurderer vi bare entallspunkter med en karakter med én verdi (funksjonen f(z) antas å være unik).

Avhengig av funksjonen til funksjonen f(z) på z -> zq Det er tre typer entallspunkter. Isolert entallspunkt zq funksjoner f(z) kalt:

1) avtagbart entallspunkt hvis det er en begrenset grense

2) stang hvis det er en grense

3) viktig poeng, hvis f(z) har verken en endelig eller uendelig grense for z-> zq.

EKSEMPEL 26.1. La oss vise at alle tre typer entallspunkter er realisert. Ta i betraktning f(z)= punkt zq = 0 er isolert

singulære poeng av denne funksjonen. Ved å bruke formel (22.12) får vi utvidelsen

hvorfra det følger at det eksisterer lim fi(z)= 1. Derfor er zq = 0

er et flyttbart entallspunkt for funksjonen fi(z).

Funksjon f'j(z) =--- har en stang i et punkt zo= 1 fordi

2 r"X

Vurder nå funksjonen )z(z)= e 1 ^ r og vis det zo = O er et essensielt enkeltpunkt for denne funksjonen. Når man strever z til null langs den reelle aksen, venstre og høyre grense for funksjonen f (z) annerledes: lim Med 1 / 1 = 0, lim med 1 /* = os. Dette innebærer,

x->0-0 x->0+O

hva f:i(z) har verken en endelig eller uendelig grense for 2 -> Å, dvs. zq = 0 er et vesentlig entallspunkt for denne funksjonen. (Merk det som poenget pleier z-iy til null på den imaginære aksefunksjonen

har ingen grense i det hele tatt.)

Selvfølgelig er det også ikke-isolerte entallspunkter. For eksempel. funksjonen har poler på punkter z n = -, P= ±1, ±2,...

Følgelig Zq = 0 er et ikke-isolert entallspunkt for denne funksjonen: i et hvilket som helst (vilkårlig lite) nabolag til dette punktet er det andre entallspunkter g s.

La zo- siste isolerte entallspunkt for en funksjon f(z). Deretter f(z) er lik i noen punktert nabolag 0 Zo av punktet zo dette nabolaget kan betraktes som en ring med indre radius r = 0. Ved teorem 25.1, i nabolaget under vurdering, funksjonen f(z) kan utvides i en Laurent-serie (25.2). Vi vil vise at oppførselen til funksjonen for 2 -> zq (dvs. typen entallspunkt zo) avhenger av formen til hoveddelen av dekomponeringen (25.2); denne omstendigheten forklarer opprinnelsen til begrepet "hoveddel".

SETING 2G.2. Et isolert entallspunkt zo av en funksjon f(z) kan fjernes hvis og bare hvis Lorap-utvidelsen i et punktert nabolag til dette punktet har oid

de. består kun av den riktige delen, og alle koeffisientene til hoveddelen er lik kulen.

Bevis. 1. La zo er et avtagbart entallspunkt. La oss bevise at Laurent utvidelse av funksjonen f(z) har formen (26.1). Siden entallspunktet zo flyttbar, så er det en begrenset grense lim f(z) = A. Følgelig f(z) avgrenset i noe punktert nabolag 0 z - zq av punktet zo, de. )(z) for alle z fra dette nabolaget. Ta noen R. U р /?|, og bruk formlene (25.3) for koeffisientene til Laurent-serien:

For koeffisientene til hoveddelen av utvidelsen n =- 1,-2,... For slike verdier P vi har p~n-e 0 kl R-> 0. Siden verdien R kan velges vilkårlig liten, da Mr~" kan være vilkårlig liten. Siden |c t,| ^ Mr~n og cn er ikke avhengig av p, da cn = 0 for og= - 1, -2,..., som skulle bevises.

2. La oss nå anta at Laurent-utvidelsen har formen (26.1). Series (26.1) er en kraftserie og. derfor konvergerer ikke bare i punkterte, men også i hele nabolaget z-zq inkludert prikken zo; beløpet S(z) er analytisk for z og S(z) = )(z) på 0 z - zo R. Derfor er det en begrenset grense lim )(z)\u003d Pm 5 (r) \u003d 5 (r) - Derfor er entallspunktet zq

Z->Zo Z-*Zo

engangs. Teoremet er bevist.

Kommentar. Det følger av beviset for teoremet at i et punktert nabolag 0 z - zo av et fjernbart entallspunkt, er funksjonen f(z) sammenfaller med funksjonen S(r), som er analytisk i hele nabolaget z - zo . Derfor, hvis vi setter /(th) = S(zq), deretter, uten å endre verdiene til funksjonen f(z) når som helst i det punkterte nabolaget gjør vi denne funksjonen analytisk i r, dvs. "fjern" funksjonen. Dette forklarer begrepet "avtakbar singularitet". Det er naturlig å betrakte slike punkter som vanlige, og ikke som entallspunkter i funksjonen f(z).

Tenk for eksempel på funksjonen

I eksempel 26.1 ble det vist at Pm (n) = 1. dvs. enkeltpunkt

zq = 0 kan fjernes. Ved å sette /i(0) = 1, eliminerer vi dermed singulariteten og får en funksjon som er analytisk på punktet zq = 0 (og i hele planet C).

La oss nå karakterisere polene når det gjelder Laurent-utvidelser.

Teorem 26.3. Et isolert entallspunkt Zo for en funksjon f(z) er en pol hvis og bare hvis, når hoveddelen av Laurent-utvidelsen med sentrum Zq har bare et begrenset antall distinkte

fra null koeffisienter med n:

Bevis. 1. La zq - pol, dvs. lim /( z) = oo.

La oss bevise at Laurent utvidelse av funksjonen f(z) har formen (2G.2). Siden lim f(z)= oo. da eksisterer det et punktert nabolag til punktet

ki zq. hvori f(z) er analytisk og har ingen nuller. Deretter funksjonen g(z) = 1 /f(z) vil også være analytisk i dette punkterte nabolaget, og lim g(z)= 0. Derfor Zo er engangs *-? *0

entallspunktet for funksjonen g(z). La oss redefinere g(z) på punktet zo, sette g(zo)= 0. Så g(z) blir analytisk i hele området rundt det (ikke punkterte) punktet z 0 , og z0 vil være dens isolerte null. Angi med N multiplisitet (rekkefølge) av denne null. Som det ble vist i §23, i nærheten av punktet zq funksjon g(z) representert i formen (se (23.2))

og (z$) f 0 og y>(z) er analytisk i et eller annet område av punktet zo- Fordi ip(z) kontinuerlig på punktet zo og g>(zo) F 0" da ip(z) har ingen nuller i et eller annet nabolag på dette punktet heller. Derfor funksjon 1 /-p(z) vil også være analytisk i dette nabolaget og utvides derfor i en Taylor-serie:

Når vi åpner parentesene og endrer betegnelsene til koeffisientene, skriver vi den siste utvidelsen i skjemaet

hvor c_jv = 1> av f 0. Dermed inneholder hoveddelen av Laurent-utvidelsen av f(r) bare et begrenset antall ledd; vi har kommet frem til nødvendig likestilling (26.2).

2. Slipp inn et punktert nabolag av et punkt th funksjon )(z) er representert ved Laurent-utvidelsen (26.2) (i en mer utvidet form, se (26.3)), hvor hoveddelen bare inneholder et begrenset antall ledd, og Med- d" f 0. Det må vi bevise Zq - funksjonsstang f(z). Multiplisere likhet (26,3) med (G - G o) iV , vi får funksjonen

Serien i (26.4) er en potensserie som konvergerer til en analytisk funksjon, ikke bare i det punkterte, men også i hele området rundt punktet Zq. Derfor funksjonen h(z) blir analytisk i dette nabolaget hvis vi utvider det i th ved å sette h(zo)= s_dg f 0. Så

Dermed er punktet o en pol, og teorem 26.3 er bevist.

Multiplisitet (rekkefølge) av null-funksjonen g(z)= 1//(r) kalles polordre funksjon /(r). Hvis en N- rekkefølgen på polen er th, da g(z)= (r - Zo)N ip(z), og gå) F 0, og, som vist i første del av beviset til setning 26.3, har utvidelsen av f(r) formen (26.3), hvor c_/v f 0. Omvendt, hvis f(r) utvides til serien (26.3) og e-z F 0, da

t.s. N- rekkefølgen på polen til funksjonen f(r). På denne måten, rekkefølgen på zq-polen til funksjonen/(G) er lik tallet på den ledende koeffisienten som ikke er null for hoveddelen av Laurent-utvidelsen i det punkterte nabolaget til punktet zq(dvs. lik et slikt tall N, hva s_dg f 0 og sp= 0 kl P > N).

La oss bevise følgende påstand, som er praktisk) for applikasjoner.

Konsekvens 26.4. Punktet zq er en pol av orden N av fiksjonen/(G) hvis og bare hvis/(G) representere i skjemaet

hvor h(z) er en analytisk funksjon i et nabolag til et punkt th og h(zo)f 0.

Bevis. Funksjon cp(z) = l/h(z) er analytisk i et eller annet nabolag til punktet r. Tilstanden til konsekvens 26.4 tilsvarer følgende:

Derfor zq - multiplisitet null N funksjoner g(z). og derav multiplisitetspolen N funksjoner /(2).

II eksempel 26.5. Finn isolerte entallspunkter for en funksjon og bestemme deres type.

D e u s sjon. Punktene der (z 2 + 1 )(z+ H) 2 = 0. Hvis z 2 L- 1 = 0 deretter 2 = ±r hvis (z 4-H) 2 = 0, da z= -3. Derfor har funksjonen tre entallspunkter z= r, 22 = -r, Z3 = - 3. Vurder z:

G - første ordens stang (vi brukte Corollary 26.4). Det kan på samme måte bevises at 22 = -Jeg også en stang av første orden. I 2 timer har vi:

La oss gå over til vurderingen av i hovedsak enkeltstående punkter.

Teorem 26.6. Et isolert entallspunkt zq av en funksjon f(z) er i hovedsak entall hvis og bare hvis hoveddelen av Laurent-utvidelsen sentrert ved zq har uendelig mange forskjellige fra. null, koeffisienter med p.

Bevis. Teorem 26.6 følger direkte av teorem 26.2 og 26.3. Faktisk, hvis poenget zq er i hovedsak entall, så kan ikke hoveddelen av Laurent-utvidelsen være fraværende eller inneholde et begrenset antall ledd (ellers er punktet Zq vil enten være avtagbar eller en stang). Derfor må antallet ledd i hoveddelen være uendelig.

Omvendt, hvis hoveddelen inneholder uendelig mange medlemmer, da Zq kan verken være et avtakbart punkt eller en stolpe. Følgelig er dette punktet i hovedsak entall.

Ifølge definisjonen kjennetegnes et vesentlig entallspunkt ved at funksjonen f(2) verken har en endelig eller uendelig grense for z ->zq. En mer fullstendig ide om hvor uregelmessig oppførselen til en funksjon er i et nabolag med et i hovedsak entallspunkt er gitt av følgende teorem.

Teorem 26.7 (Sochockis teorem). Hvis zq i hovedsak er entall, så er punktet til funksjonen f(z), deretter for et hvilket som helst komplekst tall L, inkludert A = oo, det er en sekvens av punktene z n slik at z n -> zo og lim f(zn) = MEN.

n->os

Bevis. Vurder først saken A = oo. I den første delen av beviset for setning 2G.2 slo vi fast at if f(z) er avgrenset i et eller annet punktert nabolag til punktet r0, da er alle koeffisientene c, n = - 1, - 2,... av hoveddelen er lik null (og følgelig er singulariteten i th fjernbar). Siden ved å anta at r0 er et vesentlig entallspunkt, er funksjonen f(r) ubegrenset i et hvilket som helst punktert nabolag til punktet r0. La oss ta noen smale nabolag 0 Z slik at f(zi) > 1 (hvis |/(r)| z - zo R/2 er det et punkt z-2 , hvor |/(dd)| > 2 osv.: i det punkterte nabolaget O 71. Det er åpenbart at rn -e go og lim /(r«) = oo. Således, i tilfellet A = oo, teorem 26.7

bevist.

La nå A f oo. Anta først at det er et punktert nabolag 0

= -åå---- vil være analytisk i dette punkterte nabolaget, og følgelig,

/(G) - MEN

følgelig er r et isolert entallspunkt for funksjonen Φ(r). La oss vise. at r0 er et vesentlig entallspunkt for Φ(r). La det være feil. Da finnes det en grense lim Φ(r), enten endelig eller uendelig. Fordi

/(r) = A + , da eksisterer også Hsh /(r), noe som motsier betingelsen

F(g) ~ :-*z 0

syn på teoremet. Dermed er r0 et vesentlig entallspunkt i funksjonen Φ(r). I henhold til det som ble bevist ovenfor, er det en sekvens av punkter r n slik at r n o og lim Φ(r n) = oo. Herfra

Vi har bevist den nødvendige påstanden under forutsetningen at f(r) F A i et eller annet punktert nabolag av punktet r. La oss nå anta at dette ikke er sant, dvs. i et hvilket som helst vilkårlig lite punktert nabolag av punktet th det er et slikt punkt G", at f(r") = A. Deretter for evt P i det punkterte nabolaget 0 f(z u) = L. Dermed er den nødvendige påstanden sann P-juo

i alle tilfeller, og teorem 26.7 er bevist.

I følge (Sokhotskys) teorem 26.7, i et hvilket som helst (vilkårlig lite) punktert nabolag til et i hovedsak entallspunkt, tar funksjonen f(r) verdier vilkårlig nær et hvilket som helst tall i det utvidede komplekse planet C.

For å studere isolerte entallspunkter er de velkjente Taylor-utvidelsene av grunnleggende elementære funksjoner ofte nyttige.

EKSEMPEL 2G.8. Bestem typen av entallspunkt zq = 0 for funksjonen

Løst og e. Vi utvider telleren og nevneren i en Taylor-serie i potenser av r. Substituerer til (22.11) 3 z i stedet for r og trekke fra 1, får vi

Ved å bruke (22.12) får vi utvidelsen av nevneren:

Serien i disse utvidelsene konvergerer i hele det komplekse planet €. Vi har

og /2(2) er analoge i et nabolag til punktet zo = 0 (og til og med i hele planet) og /2(20) F 0, da h(z) er også analytisk i noen områder av punktet gF 0. I følge konsekvens 26.4 er punktet Zo = 0 er bestillingens pol N = 4.

II eksempel 26.9. Finn enkeltpunkter for en funksjon f(z)= sin j - og bestemme deres type.

P e in e og e. Funksjonen har et enkelt siste entallspunkt zq = 1. På andre punkter fra C, funksjonen w =--- analytisk; derav syndfunksjonen w vil være analytisk.

Substituere i utvidelsen av sinus (22.12) - i stedet for r, får vi

Vi har oppnådd utvidelsen av sin funksjon i en Laurent-serie i et punktert nabolag av punktet 20 = 1. Siden den resulterende utvidelsen inneholder uendelig mange ledd med negative potenser (r - 1), så zq = 1 er et vesentlig entallspunkt (i dette tilfellet består Laurent-utvidelsen bare av hoveddelen, og den riktige delen mangler).

Merk at i dette tilfellet var det også mulig å fastslå singularitetens natur direkte fra definisjonen, uten å ty til serieutvidelse. Det er faktisk sekvenser (r") og (2") som konvergerer til zo= 1, og slik at f(z" n)= 1, /(2") = 0 (spesifiser slike sekvenser selv). Så, f(z) har ingen grense når z -> 1 og derav poenget zq - 1 er i hovedsak entall.

La oss introdusere konseptet med en Laurent-utvidelse av en funksjon i et nabolag til et punkt Zq = 00 og vurder sammenhengen mellom utvidelsen og singularitetens natur på dette punktet. Merk at definisjonene av et isolert entallspunkt og dets type (avtakbar, pol eller i hovedsak entall) overføres til saken zq = oc uendret. Men teoremer 26.2. 26.3 og 26.6, relatert til Laurent-utvidelsenes natur, må endres. Poenget er at medlemmene c n (z - 2o) s. P= -1,-2,..., hoveddelen, som definerer "'uregelmessigheten" til funksjonen nær sluttpunktet Zq, ettersom 2 har en tendens til å oo, vil de oppføre seg "riktig" (pleier til 0). Tvert imot medlemmene av den vanlige delen med P= 1,2,... vil ha en tendens til å oo; de bestemmer arten av singulariteten i Zq = oo. Derfor vil hoveddelen av utvidelsen i nabolaget til oo være vilkårene med positive krefter P, og riktig - med negativ.

La oss introdusere en ny variabel w = 12. Funksjon tv= 1/2, utvidet slik at u(oo) = 0, en-til-en og konformt kartlegger nabolaget z > R poeng zq = 00 i nærheten av |w| wq = 0. Hvis funksjonen f(z) analyser i et punktert nabolag R z Zq = oc, deretter funksjonen G(w) = f(l/w) vil være analytisk i det gule nabolaget 0 wo = 0. Siden for 2 -> oo vil det være w-> 0, da

Derfor G(w) har på punktet wq = 0 er en singularitet av samme type som f(z) på punktet Zq = 00. La oss utvide funksjonen G(w) i en Laurent-serie i et punktert nabolag til punktet wo = 0:

Summene på høyre side av (26.5) representerer henholdsvis riktig og hoveddel av utvidelsen. La oss gå videre til variabelen z, erstatte w = 1/z:

angir P\u003d -A *, 6 * \u003d 6_ " \u003d med s og merker det G(l/z) = f(z), vi får

Dekomponeringen (2G.G) kalles Laurent utvidelse av funksjonen f(z) i et punktert nabolag til punktet zq= oo. Den første summen i (2G.6) kalles høyre del, og den andre summen er hoveddel denne nedbrytningen. Siden disse summene tilsvarer de korrekte og hoveddelene av utvidelsen (26.5), tilfredsstiller utvidelsen (26.6) analogene til teoremene 26.2, 26.3 og 26.6. Følgende teorem er således en analog til teorem 26.2.

Teorem 26.10. Isolert entallspunktZq - os (funksjoner/(G) kan fjernes hvis og bare hvis Laurent-utvidelsen i et punktert nabolag på dette punktet har formen

t.s. består kun av den riktige delen.

Vi setter /(oo) = co. Funksjonen definert av serien (26.7) som konvergerer i nabolaget z > R punkter 2o \u003d oc, kalt analytisk ved punktet z o = oo. (Merk at denne definisjonen tilsvarer analytisiteten til funksjonen G(w) på punktet wo = 0.)

Eksempel 26.11. Undersøk entallspunktet zq = oo til funksjonen

Siden grensen er begrenset, altså zo = oo er et fjernbart singularpunkt for funksjonen f(r). Hvis vi setter /(oo) = lim J(z)= 0, da f(z) vil bli

tic på punktet Zo= os. La oss vise hvordan du finner den tilsvarende utvidelsen (26.7). La oss gå videre til variabelen w = 1 fz. Erstatter z= 1 /?e, får vi

(den siste likheten er gyldig i det punkterte området til punktet ww = 0, men vi utvider definisjonen (7(0) = 0). Den resulterende funksjonen har entallspunkter w =±jeg, w =-1/3, og på punktet Wq = 0 er analytisk. Utvidende funksjon G(w) av grader w(som ble gjort i eksempel 25.7) og substituering i den resulterende potensserien w = 1/z man kan få utvidelsen (26.7) av funksjonen f(z).

Teorem 26.3 for saken zo= oo vil bli omskrevet i følgende form.

Teorem 26.12. Isolert entallspunkt gå = os funksjon f(z) er en pol hvis og bare hvis hoveddelen av Laurent-utvidelsen (26.6) har bare et begrenset antall koeffisienter som ikke er null Med":

Her er serien den vanlige delen, og polynomet i parentes er hoveddelen av utvidelsen. Multiplisiteten til polen i oc er definert som multiplisiteten til polen wq = 0 funksjoner G(z). Det er lett å se at multiplisiteten til polen sammenfaller med tallet N i (26.8).

Q p | (i 2 + 1) (z + 3) 2

En oppgave. Vis at funksjonen f(z) =-- -- har inne

punkt zo = oo polordre 3.

Teorem 26.6 om et essensielt entallspunkt er skrevet om for saken zo= os nesten ordrett, og vi dveler ikke ved det i detalj.

Grunnleggende begreper og definisjoner:

Nullpunktet til den analytiske funksjonen f(z) er punktet "a" for hvilket f(a)=0.

Null i orden "n" til funksjonen f(z) er punktet "a" hvis men fn(a)¹0.

Et entallspunkt "a" kalles et isolert entallspunkt for funksjonen f(z) hvis det eksisterer et nabolag til dette punktet hvor det ikke er noen entallspunkter annet enn "a".

Isolerte entallspunkter er av tre typer: .

1 avtagbare spesialpunkter;

3 essensielle entallspunkter.

Typen av et entallspunkt kan bestemmes basert på oppførselen til den gitte funksjonen ved det funnet entallspunktet, så vel som fra formen til Laurent-serien oppnådd for funksjonen i nærheten av det funnet entallspunktet.

Bestemme typen av et entallspunkt ved oppførselen til funksjonen i det.

1. Fjernbare entallspunkter.

Et isolert entallspunkt a av funksjonen f(z) kalles flyttbart hvis det finnes en endelig grense .

2. Polakker.

Et isolert entallspunkt a i funksjonen f(z) kalles en pol if .

3. Betydelige entallspoeng.

Et isolert singularpunkt a av en funksjon f(z) kalles et essensielt singularpunkt hvis verken finitt eller uendelig eksisterer.

Følgende relasjon finner sted mellom nullpunktene og polene til funksjonen.

For at et punkt a skal være en pol av orden n av funksjonen f(Z), er det nødvendig og tilstrekkelig at dette punktet er en null av orden n for funksjonen.

Hvis n=1 kalles polen enkel.

Definisjon: Et isolert entallspunkt med en karakter med én verdi kalles:

a) kan fjernes hvis hoveddelen av dekomponeringen er fraværende;

b) en stolpe hvis hoveddelen inneholder et begrenset antall medlemmer;

c) et vesentlig singulart punkt hvis hoveddelen inneholder et uendelig antall ledd.

a) I et nabolag med et flyttbart entallspunkt har utvidelsen således formen:

det uttrykker funksjonen ved alle punkter i sirkelen |z-a|

Ved sentrum z=a er likheten falsk, fordi funksjonen ved z=a har en diskontinuitet, og høyre side er kontinuerlig. Hvis verdien av funksjonen i midten endres, og tar den lik verdien på høyre side, vil gapet bli eliminert - derav navnet - kan fjernes.

b) I nærheten av en pol av orden m har ekspansjonen av Laurent-serien formen:

c) I nærheten av en enkel stolpe

Fradrag og formler for deres beregning.

Residuet av en analytisk funksjon f(z) ved et isolert entallspunkt z 0 er et komplekst tall lik verdien av integralet , tatt i positiv retning langs sirkelen L sentrert ved punktet z 0 , som ligger i analytisitetsområdet til funksjonen f(z) (dvs. i ringen 0)<|z-z0|

Resten av funksjonen f(z) ved et isolert entallspunkt z 0 er angitt med symbolet Res f(z 0) eller Res (f(z); z 0). På denne måten,

Resf(z0)= . (22.15.1)

Hvis vi setter n=-1 i formelen (22.15.1), får vi:

C-1=

eller Res f(z 0)= C-1,

de. resten av funksjonen f(z) med hensyn til entallspunktet z 0 er lik koeffisienten til det første leddet med en negativ eksponent i utvidelsen av funksjonen f(z) i en Laurent-serie.

Beregning av fradrag.

Vanlige eller avtagbare entallspunkter. Det er klart, hvis z=z 0 er et regulært eller fjernbart singularpunkt for funksjonen f(z), så er Res f(z 0)=0 (det er ingen hoveddel i Laurent-dekomponeringen i disse tilfellene, så c-1= 0).

Stang. La punktet z 0 være en enkel pol til funksjonen f(z). Da har Laurent-serien for funksjonen f(z) i et nabolag til punktet z 0 formen:

Herfra

Derfor får vi ved å passere inn denne likheten til grensen som z --z 0

Oppløsning f(z0)=

Egentlig spesielt poeng. Hvis punktet z 0 er et vesentlig singularpunkt for funksjonen f(z), så for å beregne resten av funksjonen på dette punktet, bestemmer man vanligvis direkte koeffisienten c-1 i utvidelsen av funksjonen i en Laurent-serie.

Klassifisering av hendelser. Sum, produkt av hendelser, deres egenskaper, grafisk representasjon.

Arrangementene er delt inn i:

1. Tilfeldig

2. Troverdig

3. Umulig

Pålitelig - dette er en hendelse som nødvendigvis oppstår under disse forholdene (natt etterfølges av morgen).

Tilfeldig er en hendelse som kan eller ikke kan forekomme (bestått en eksamen).

Det umulige er en hendelse som ikke vil skje under de gitte forholdene (få en grønn blyant ut av esken med bare røde).

enkeltpunkt

i matematikk.

1) Enkeltpunkt for kurven gitt av ligningen F ( x, y) = 0, - punkt M 0 ( x 0, y 0), der begge partielle deriverte av funksjonen F ( x, y) forsvinne:

Hvis i tillegg ikke alle andre partielle deriverte av funksjonen F ( x, y) i punktet M 0 er lik null, så kalles O. t. dobbel. Hvis, sammen med forsvinningen av de første deriverte ved punktet M 0, forsvinner alle de andre derivertene, men ikke alle de tredje derivertene er lik null, kalles O. t. trippel, og så videre. Når du studerer strukturen til en kurve nær en dobbel O. t., spilles en viktig rolle av tegnet til uttrykket

Hvis Δ > 0, kalles O. t. isolert; for eksempel kurven y 2 - x 4 + 4x 2= 0 opprinnelsen er en isolert O. t. (se ris. en ). Hvis Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - a 4= 0 opprinnelsen til koordinatene er nodal O. t. (se ris. 2 ). Hvis Δ = 0, så er O. t.-kurven enten isolert eller karakterisert ved at forskjellige grener av kurven har en felles tangent på dette punktet, for eksempel: tangent og danner et punkt, som en kurve y 2 - x 3= 0 (se ris. 3 , a); b) cusp av den andre typen - forskjellige grener av kurven er plassert på samme side av den felles tangenten, som en kurve (y - x 2)2 x 5= 0 (se ris. 3 , b); c) selvkontaktpunkt (for en kurve y 2 - x 4= 0 opprinnelse er et punkt for selvkontakt; (cm. ris. 3 , i). Sammen med den angitte O. t. finnes det mange andre O. t. med spesielle navn; for eksempel er et asymptotisk punkt toppen av en spiral med et uendelig antall svinger (se fig. ris. fire ), knekkpunkt, hjørnepunkt osv.

2) Et entallspunkt i en differensialligning er et punkt der både telleren og nevneren på høyre side av differensialligningen forsvinner samtidig (se differensialligninger)

hvor P og Q er kontinuerlig differensierbare funksjoner. Forutsatt at O. t. ligger ved opprinnelsen til koordinatene og bruker Taylor-formelen (se Taylor-formelen), kan vi representere ligning (1) i formen

hvor P 1 ( x, y) og Q 1 ( x, y) er uendelig små med hensyn til

Nemlig, hvis λ 1 ≠ λ 2 og λ 1 λ 2 > 0 eller λ 1 = λ 2, så er O. t. en node; alle integralkurver som går gjennom punkter i et tilstrekkelig lite nabolag av noden, kommer inn i det. Hvis λ 1 ≠ λ 2 og λ 1 λ 2 i β, α ≠ 0 og β ≠ 0, så er O. t. et fokus; alle integralkurver som går gjennom punkter i et tilstrekkelig lite nabolag av fokuset er spiraler med et uendelig antall svinger i et hvilket som helst vilkårlig lite nabolag av fokuset. Hvis til slutt, λ 1,2 = ± Jegβ, β ≠ 0, så er ikke karakteren til O. t. bestemt av lineære termer i utvidelser av P ( x, y) og Q ( x, y), slik tilfellet var i alle de ovennevnte tilfellene; her kan O. t. være et fokus eller senter, eller det kan ha en mer kompleks karakter. I nabolaget til sentrum er alle integrerte kurver lukket og inneholder sentrum inne i dem. Så for eksempel er punktet (0, 0) en node for ligningene på" = 2u/x(λ 1 = 1, λ 2 = 2; se ris. 5 , a) og y" = u/x(λ 1 = λ 2 = 1; se ris. 5 , b), en sal for ligningen y" = -y/x(λ 1 = -1, λ 2 = 1 ; cm. ris. 6 ), fokuset for ligningen y" =(x + y) / (x - y) (λ 1 = 1 - Jeg, λ2 = 1+ Jeg; cm. ris. 7 ) og sentrum for ligningen y" = -x / y(λ 1 = -Jeg, λ2 = Jeg; cm. ris. åtte ).

Hvis x, y) og Q ( x, y) er analytiske, kan området til en O. t. av høyere orden deles inn i regioner: D 1 - fylt med integrerte kurver, begge ender går inn i O. t. (elliptiske områder), D 2 - fylt med integralkurver, den ene enden går inn i O. t. (parabolske områder), og D 3 - områder avgrenset av to integralkurver inkludert i O. t., mellom hvilke det er integralkurver av typen hyperbler (hyperboliske områder) (se. ris. 9 ). Hvis det ikke er integralkurver som går inn i et O.-punkt, kalles O.-punktet et punkt av stabil type. Nabolaget til en stabil O. t. består av lukkede integrerte kurver som inneholder O. t. inne i seg selv, mellom hvilke spiraler er plassert (se fig. ris. ti ).

Studiet av O. t. differensialligninger, dvs. i hovedsak studiet av oppførselen til familier med integrerte kurver i et nabolag av O. t. M. Lyapunov a, A. Poincaré og andre).

3) Et enkeltpunkt i en analytisk funksjon med én verdi er et punkt der funksjonens analytisitet brytes (se Analytiske funksjoner). Hvis det er et nabolag av O. t. en, fri for andre O. t., så punktet en kalles isolert O. t. If en er en isolert O.T. og det eksisterer en endelig O.T. kalles en flyttbar O.T. Ved passende å endre definisjonen av funksjonen i punktet a (eller omdefinere den på dette punktet, hvis funksjonen ikke er definert i det hele tatt), nemlig å sette f(en)= b, er det mulig å oppnå en vil bli et vanlig punkt for den korrigerte funksjonen. For eksempel, prikk z= 0 er en fjernbar O.T. for funksjonen f 1 ( z) = f(z), hvis z≠ 0, og f 1(0),=1, prikk z= 0 er et vanlig punkt [ f 1 (z) er analytisk på punktet z= 0]. Hvis en en- isolert O. t. og a kalles en pol eller et uvesentlig enkeltpunkt i funksjonen f(z), hvis Laurent-serien) fungerer f(z) i et nabolag av en isolert O. t. inneholder ikke negative potenser z - a, hvis en- fjernbar O. t., inneholder et begrenset antall negative potenser z - a, hvis en- stang (i dette tilfellet rekkefølgen på stangen R er definert som den høyeste potensen til a - et i hovedsak entallspunkt. For eksempel for funksjonen

p = 2, 3, …)

punktum z= 0 er ordenens pol R, for funksjonen

punktum z= 0 er et vesentlig entallspunkt.

På grensen til konvergenssirkelen til en potensrekke må det være minst en O. t. av funksjonen representert inne i denne sirkelen av den gitte potensserien. Alle grensepunkter for eksistensdomenet til en enkeltverdi analytisk funksjon (naturlig grense) er grensepunkter for denne funksjonen. Dermed sirkler alle punktene i enheten | z| = 1 er spesielle for funksjonen

For en multi-verdi analytisk funksjon, konseptet "O. t." vanskeligere. I tillegg til O. t., i individuelle ark av Riemann-overflaten til en funksjon (det vil si O. t. av enkeltverdige analytiske elementer), er ethvert grenpunkt også en O. t. av funksjonen. Isolerte grenpunkter av en Riemann-overflate (dvs. grenpunkter slik at det i noen av deres nabolag ikke er andre O.t.-funksjoner i noe blad) er klassifisert som følger. Hvis a er et isolert grenpunkt av endelig orden og det eksisterer en endelig a, kalles det en kritisk pol. Hvis en en er et isolert grenpunkt av uendelig rekkefølge, og a kalles en transcendental O. t. Alle andre isolerte grenpunkter kalles kritiske essensielt singulære punkter. Eksempler: prikk z= 0 er et vanlig kritisk punkt for funksjonen f ( z) = logg z og et kritisk essensielt enkeltpunkt for funksjonen f (z) = sin log z.

Enhver O. t., bortsett fra en fjernbar en, er en hindring for analytisk fortsettelse, dvs. analytisk fortsettelse langs en kurve som går gjennom en ikke-fjernbar O. t. er umulig.

Stor sovjetisk leksikon. - M.: Sovjetisk leksikon. 1969-1978 .

Se hva "Special Point" er i andre ordbøker:

Poeng her. Se også entallspunkt (differensialligninger). Et trekk eller singularitet i matematikk er et punkt der et matematisk objekt (vanligvis en funksjon) ikke er definert eller har uregelmessig oppførsel (for eksempel et punkt der ... ... Wikipedia

En analytisk funksjon er et punkt der vilkårene for analytisitet brytes. Hvis en analytisk funksjon f(z) er definert i et eller annet område av punktet z0 overalt … Fysisk leksikon

En analytisk funksjon er punktet der analytisiteten til en funksjon blir krenket ... Stor encyklopedisk ordbok

enkeltpunkt- — [Ya.N. Luginsky, M.S. Fezi Zhilinskaya, Yu.S. Kabirov. English Russian Dictionary of Electrical Engineering and Power Industry, Moskva, 1999] Elektrotekniske emner, grunnleggende konsepter EN entall ... Teknisk oversetterhåndbok

1) En OT for en analytisk funksjon f(z) er en hindring for den analytiske fortsettelsen av et element av funksjonen f(z) til en kompleks variabel z langs en eller annen bane i planet til denne variabelen. La den analytiske funksjonen f(z) være definert av noen ... ... Matematisk leksikon

En analytisk funksjon, punktet der funksjonens analytisitet blir krenket. * * * ENKEL PUNKT ET ENKEL PUNKT for en analytisk funksjon, et punkt der funksjonens analytisitet blir krenket ... encyklopedisk ordbok

enkeltpunkt- ypatingasis taškas statusas T sritis automatika atitikmenys: engl. entall punkt vok. singularer Punkt, m rus. entallspunkt, fpranc. punktpartikkel, m; point singulier, m … Automatikos terminų žodynas

enkeltpunkt- ypatingasis taškas statusas T sritis fizika atitikmenys: engl. entall punkt vok. singularer Punkt, m rus. entallspunkt, fpranc. point singulier, m … Fizikos terminų žodynas

Taylor-serien fungerer som et effektivt verktøy for å studere funksjoner som er analytiske i sirkelen zol For å studere funksjoner som er analytiske i et ringformet område, viser det seg at det er mulig å konstruere utvidelser i positive og negative potenser (z - zq) av form som generaliserer Taylor-utvidelser. Serien (1), forstått som summen av to serier, kalles Laurent-serien. Det er klart at konvergensregionen til serie (1) er den felles delen av konvergensregionene til hver av seriene (2). La oss finne henne. Konvergensområdet til den første serien er en sirkel hvis radius bestemmes av Cauchy-Hadamard-formelen Inne i konvergenssirkelen konvergerer serie (3) til en analytisk funksjon, og i enhver sirkel med mindre radius konvergerer den absolutt og jevnt. Den andre serien er en potensrekke med hensyn til variabelen. Serien (5) konvergerer innenfor sin konvergenskrets til den analytiske funksjonen til den komplekse variabelen m-*oo, og i enhver sirkel med mindre radius konvergerer den absolutt og jevnt, som betyr at konvergensområdet til serien (4) er utseendet til sirkelen - Hvis det da er et felles område for konvergens av serien (3) og (4) - en sirkulær ring der serien (1) konvergerer til en analytisk funksjon. Dessuten, i enhver ring, konvergerer den absolutt og jevnt. Eksempel 1. Bestem konvergensområdet for rad Laurent-serien. Isolerte entallspunkter og deres klassifisering (z), som er enverdi og apolitisk i en sirkulær ring, kan representeres i denne ringen som summen av en konvergent serie hvis koeffisienter Cn er unikt bestemt og beregnet av formlene der 7p er en sirkel med radius m La oss fikse et vilkårlig punkt z inne i ringen R Vi konstruerer sirkler med senter i punktet r0 hvis radier tilfredsstiller ulikhetene og tar for oss en ny ring I følge Cauchy-integralsetningen for et multiplisert domene har vi La oss transformere hver av integralene i summen (8) separat. For alle punktene £ langs sirkelen 7d* er relasjonen de summen av en jevnt konvergent serie 1 1 oppfylt. Derfor kan brøken ^ representeres i vi- /" / For alle punktene £ på sirkelen ir> relasjonen er oppfylt Derfor kan brøken ^ representeres som summen av en jevnt konvergent serie i formlene (10) og (12) er analytiske funksjoner i en sirkulær ring. Derfor, ved Cauchys teorem, endres ikke verdiene til de tilsvarende integralene hvis sirklene 7/r og 7r/ erstattes av en hvilken som helst sirkel. Dette gjør at vi kan kombinere formlene (10) og (12) Ved å erstatte integralene på høyre side av formel (8) med deres uttrykk (9) og (11), får vi den ønskede utvidelsen Siden z er en vilkårlig punkt av ringen, følger det at serien ( 14) konvergerer til funksjonen f(z) overalt i denne ringen, og i enhver ring konvergerer serien til denne funksjonen absolutt og jevnt. La oss nå bevise at dekomponeringen av formen (6) er unik. Anta at det skjer en dekomponering til. Da, overalt inne i ringen R, har vi På omkretsen konvergerer serien (15) jevnt. Multipliser begge sider av likheten (der m er et fast heltall, og integrer begge serieledd for ledd. Som et resultat får vi på venstre side, og på høyre side - Csh. Dermed, (4, \u003d St. Siden m er et vilkårlig tall, kalles den siste likhetsserien (6), hvis koeffisienter beregnes med formler (7), Laurent-serien til funksjonen f(z) i ringen 7) for koeffisientene til Laurent-seriene brukes sjelden i praksis, fordi de som regel krever tungvinte beregninger. Vanligvis, hvis mulig, brukes ferdige Taylor-utvidelser av elementære funksjoner. Basert på utvidelsens unike, fører enhver legitim metode til det samme resultat Eksempel 2 Betrakt Laurent-seriens utvidelser av funksjonene til forskjellige domener, forutsatt at Fuiscija /(z) har to entallspunkter: Derfor er det tre ringdomener og sentrert i punktet r = 0. i hver av funksjonen f(r) er analytisk: a) sirkelen er sirkelens ytre (fig. 27). La oss finne Laurent-utvidelsene av funksjonen /(z) i hver av disse regionene. Vi representerer /(z) som en sum av elementære brøker a) Sirkeltransformasjonsrelasjon (16) som følger Ved å bruke formelen for summen av leddene til en geometrisk progresjon får vi b) Ringen for funksjonen -z forblir konvergent i denne ringen, siden Serie (19) for funksjonen j^j for |z| > 1 divergerer. Derfor transformerer vi funksjonen /(z) som følger: ved å bruke formel (19) igjen, får vi det Denne serien konvergerer for. Ved å erstatte utvidelsene (18) og (21) i relasjon (20), får vi c) Sirkelens eksteriøritet for funksjonen -z med |z| > 2 divergerer, og serier (21) for funksjonen La oss representere funksjonen /(z) i følgende form: /<*>Ved å bruke formlene (18) og (19), får vi OR 1. Dette eksemplet viser at for samme funksjon f(z) har Laurent-utvidelsen generelt sett annen type for forskjellige ringer. Eksempel 3. Finn dekomponeringen av de 8 Laurent-seriene til funksjonen Laurent-serien Isolerte entallspunkter og deres klassifisering i det ringformede området A. Vi bruker representasjonen av funksjonen f (z) i følgende form: og transformer det andre leddet. formel for summen av leddene til en geometrisk progresjon, får vi. Ved å erstatte de funnet uttrykkene i formelen (22), har vi eksempel 4. Utvid funksjonen i en Laurent-serie i nærheten av tynn zq = 0. For en hvilken som helst kompleks en , vi har La Denne utvidelsen er gyldig for ethvert punkt z Ф 0. I dette tilfellet er det ringformede området hele det komplekse planet med ett punkt z kastet ut - 0. Dette området kan defineres av følgende forhold: Denne funksjonen er analytisk i regionen Fra formler (13) for koeffisientene til Laurent-serien, med samme resonnement som i forrige avsnitt, kan man få Kouiw-ulikhetene. hvis funksjonen f(z) er avgrenset på en sirkel, der M er en konstant), så kalles isolerte entallspunkter Et punkt zo et isolert entallspunkt for funksjonen f(z) hvis det eksisterer et ringformet nabolag til punktet ( Dette settet kalles noen ganger også et gjennomhullet nabolag til punktet 2o), der funksjonen f(z) er enkeltverdi og analytisk. På selve punktet zo er funksjonen enten ikke definert eller er ikke enverdig og analytisk. Tre typer entallspunkter skilles avhengig av oppførselen til funksjonen /(z) når man nærmer seg punktet zo. Et isolert singularpunkt kalles: 1) fjernbart hvis det finnes en endelig 2) pmusach hvis 3) et vesentlig singularpunkt hvis funksjonen f(z) ikke har noen grense for Teorem 16. Et isolert singularpunkt z0 av en funksjon f(z) er et fjernbart singularpunkt hvis og bare hvis Laurent-utvidelsen av funksjonen f(z) i et nabolag til punktet zo ikke inneholder en hoveddel, dvs. har formen Let zo - avtagbart entallspunkt. Da eksisterer det en endelig, og derfor er funksjonen f(z) avgrenset i et prokologisk nabolag til punktet r. Vi setter i kraft av Cauchy-ulikhetene Siden det er mulig å velge p som vilkårlig liten, så er alle koeffisienter ved negative potenser (z - 20) er lik null: Omvendt, la Laurent-utvidelsen av funksjonen /(r) i et nabolag av punktet zq inneholder bare den korrekte delen, dvs. den har formen (23) og derfor , er Taylor. Det er lett å se at for z -* z0 har funksjonen /(r) en grenseverdi: Teorem 17. Et isolert entallspunkt zq av funksjonen f(z) kan fjernes hvis og bare hvis funksjonen J(z) er avgrenset i noen punktert nabolag av punktet zq, Zgmechai ikke. La r0 være et fjernbart entallspunkt av f(r). Forutsatt at vi får at funksjonen f(r) er analytisk i en sirkel sentrert i punktet th. Dette definerer navnet på punktet - engangs. Teorem 18. Et isolert entallspunkt zq av en funksjon f(z) er en pol hvis og bare hvis hoveddelen av Laurent-utvidelsen av funksjonen f(z) i et nabolag av punktet inneholder et endelig (og positivt) tall av ledd som ikke er null, dvs. har formen 4 La z0 være en pol. Siden da eksisterer det et punktert nabolag til punktet z0 der funksjonen f(z) er analytisk og ikke null. Deretter er en analytisk funksjon definert i dette nabolaget, og derfor er punktet zq et fjernbart entallspunkt (null) av funksjonen eller hvor h(z) er en analytisk funksjon, er h(z0) ∩ 0. analytisk i et nabolag av punktet zq, og derav hvorfra vi får det La oss nå anta at funksjonen f(z) har en dekomponering av formen (24) i et punktert nabolag til punktet zo. Dette betyr at i dette nabolaget er funksjonen f(z) analytisk sammen med funksjonen. For funksjonen g(z) er ekspansjonen gyldig hvorfra det er klart at zq er et fjernbart singularpunkt for funksjonen g(z) og eksisterer. Deretter tenderer funksjonen til 0 - polen til funksjonen Det er en enkel til faktum. Punktet Zq er en pol til funksjonen f(z) hvis og bare hvis funksjonen g(z) = y kan utvides til en analytisk funksjon i et nabolag til punktet zq ved å sette g(z0) = 0. Rekkefølgen av polen til funksjonen f(z) kalles nullordenen til funksjonen jfa. Teoremer 16 og 18 innebærer følgende påstand. Teorem 19. En isolert entall tynn er i hovedsak entall hvis og bare hvis hoveddelen av Laurent-utvidelsen i et punktert nabolag av dette punktet inneholder uendelig mange termer som ikke er null. Eksempel 5. Entallspunktet til funksjonen er zo = 0. Vi har Laurent-serien isolerte entallspunkter og deres klassifisering. Derfor er zo = 0 et fjernbart entallspunkt. Utvidelsen av funksjonen /(z) i en Laurent-serie i nærheten av nullpunktet inneholder kun den korrekte delen: Eksempel7. f(z) = Entallspunktet til funksjonen f(z) er zq = 0. Vurder oppførselen til denne funksjonen på den reelle og den imaginære aksen: på den reelle aksen ved x 0, på den imaginære aksen Derfor er verken endelig eller imaginær. uendelig grense f(z) ved z -* 0 eksisterer ikke. Derfor er punktet r0 = 0 et vesentlig singularpunkt for funksjonen f(z). La oss finne Laurent-utvidelsen av funksjonen f(z) i et nabolag til nullpunktet. For enhver kompleks C har vi satt. Da inneholder Laurent-utvidelsen et uendelig antall ledd med negative potenser z.