Модели, описани от системи от две автономни диференциални уравнения.

фазова равнина. Фазов портрет. метод на изоклина. главни изоклини. Стабилно състояние. Линейни системи. Типове ключови точки: възел, седло, фокус, център. Пример: химична реакцияпърва поръчка.

Най-интересните резултати при качественото моделиране на свойствата на биологичните системи са получени върху модели на две диференциални уравнения, които позволяват качествено изследване с помощта на метода фазова равнина. Да разгледаме система от две автономни обикновени диференциални уравнения от общ вид

(4.1)

P(x,y), Q(x,y)- непрекъснати функции, дефинирани в някаква област ЖЕвклидова равнина ( x,y- декартови координати) и имащи в тази област непрекъснати производни от ред не по-нисък от първия.

Регион Жможе да бъде неограничен или ограничен. Ако променливите x, yимат конкретно биологично значение (концентрации на вещества, изобилие на видове), най-често площта Же положителният квадрант на дясната полуравнина:

0 £ х< ¥ ,0 £ г< ¥ .

Концентрациите на веществата или изобилието от видове също могат да бъдат ограничени отгоре от обема на съда или от площта на местообитанието. Тогава диапазонът от променливи има формата:

0 £ х< x 0 , 0 £ г< y 0 .

Променливи x, yпромяна във времето в съответствие със системата от уравнения (4.1), така че всяко състояние на системата съответства на двойка стойности на променливи ( x, y).

Обратно, за всяка двойка променливи ( x, y) съответства на определено състояние на системата.

Помислете за равнина с координатни оси, върху които са нанесени стойностите на променливите x,y. Всяка точка Мтази равнина съответства на определено състояние на системата. Такава равнина се нарича фазова равнина и изобразява съвкупността от всички състояния на системата. Точката M(x, y) се нарича изобразяваща или изобразяваща точка.

Нека в началния момент t=t 0 представлява координатите на точката М 0 (х(T 0),г(T 0)). Във всеки следващ момент във времето Tизобразяващата точка ще се движи според промените в стойностите на променливите х(T),г(T). Набор от точки М(х(T), y(t)) на фазовата равнина, чиято позиция съответства на състоянията на системата в процеса на промяна на променливите във времето x(t), y(t)съгласно уравнения (4.1), се нарича фазова траектория.

Наборът от фазови траектории за различни начални стойности на променливите дава лесно видим "портрет" на системата. Сграда фазов портретви позволява да правите заключения за естеството на промените в променливите x, yбез да познава аналитичните решения на оригиналната система от уравнения(4.1).

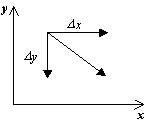
За да се изобрази фазов портрет, е необходимо да се изгради векторно поле от посоки за траекториите на системата във всяка точка от фазовата равнина. Чрез посочване на увеличениед t>0,получаваме съответните увеличения д хи д гот изрази:

д x=P(x,y)д T,

д y=Q(x,y)д T.

векторна посока dy/dxв точка ( x, y) зависи от знака на функциите P(x, y), Q(x, y)и може да се даде чрез таблица:

P(x,y)>0,Q(x,y)>0
P(x,y)<0,Q(x,y)<0
P(x,y)>0,Q(x,y)<0
P(x,y)<0,Q(x,y)>0

.(4.2)

Решение на това уравнение y=y(x, c), или имплицитно Е(x,y)=c,където се константата на интегриране, дава семейството от интегрални криви на уравнение (4.2) - фазови траекториисистема (4.1) на самолета x, y.

Изоклинен метод

За да се изгради фазов портрет, се използва метод на изоклина -на фазовата равнина са начертани линии, които пресичат интегралните криви под един определен ъгъл. Уравнението на изоклина се получава лесно от (4.2). Да сложим

където НО– определена константа. Значение НОпредставлява тангенса на наклона на допирателната към фазовата траектория и може да приема стойности от -¥ до + ¥ . Заместване вместо dy/dxв (4.2) количеството НОполучаваме уравнението на изоклина:

.(4.3)

Уравнение (4.3) определя във всяка точка на равнината единствената допирателна към съответната интегрална крива, с изключение на точката, където P(x,y)= 0, Q (x,y) = 0 , в която посоката на тангентата става неопределена, тъй като стойността на производната става неопределена:

.

Тази точка е пресечната точка на всички изоклини - специална точка.Той едновременно заличава времевите производни на променливите хи г.

Така в сингулярната точка скоростите на промяна на променливите са равни на нула. Следователно, сингулярната точка на диференциалните уравнения на фазовите траектории (4.2) съответства на стационарно състояние на системата(4.1), а координатите му са стационарните стойности на променливите x, y.

Особен интерес представляват главни изоклини:

dy/dx=0, P(x,y)=0 – изоклина на хоризонтални допирателни и

dy/dx=¥ , Q(x,y)=0 – изоклина на вертикални тангенти.

Чрез построяване на главните изоклини и намиране на пресечната им точка (x,y), чиито координати отговарят на условията:

така ще намерим пресечната точка на всички изоклини на фазовата равнина, в която посоката на допирателните към фазовите траектории е неопределена. То - сингулярна точка, което съответства стационарно състояние на системата(фиг. 4.2).

Системата (4.1) има толкова стационарни състояния, колкото са пресечните точки на главните изоклини на фазовата равнина.

Всяка фазова траектория съответства на набор от движения на динамична система, преминаващи през едни и същи състояния и различаващи се едно от друго само в началото на времевата референция.

Ако условията на теоремата на Коши са изпълнени, тогава през всяка точка от пространството x, y, tпреминава през една интегрална крива. Същото важи, благодарение на автономността, за фазовите траектории: уникална фазова траектория преминава през всяка точка от фазовата равнина.

Стабилно състояние

Нека системата е в равновесие.

Тогава представителната точка се намира в една от сингулярните точки на системата, в която по дефиниция:

.

Дали една особена точка е стабилна или не се определя от това дали представителната точка напуска или не с малко отклонение от стационарното състояние. Приложено към система от две уравнения, определението за стабилност в езикад, дкакто следва.

Равновесното състояние е стабилно, ако за дадена област има отклонения от равновесното състояние (д )може да се посочи площ д (д ), заобикалящ състоянието на равновесие и притежаващ свойството да няма траектория, която да започва вътре в региона д , никога няма да стигне до границата д . (фиг. 4.4)

За голям клас системи - груби системи – естеството на поведението на което не се променя с малка промяна във вида на уравненията, информация за вида на поведението в близост до стационарното състояние може да бъде получена чрез изучаване не на оригинала, а на опростения линеаризирансистема.

Линейни системи.

Помислете за система от две линейни уравнения:

.(4.4)

Тук a, b, c, d- константи, x, y- Декартови координати на фазовата равнина.

Общото решение ще се търси във формата:

.(4.5)

Заместете тези изрази в (4.4) и намалете с д л T:

(4.6)

Алгебрична система от уравнения (4.6) с неизвестни А, Бима ненулево решение само ако неговата детерминанта, съставена от коефициентите на неизвестните, е равна на нула:

.

Разширявайки тази детерминанта, получаваме характеристичното уравнение на системата:

.(4.7)

Решението на това уравнение дава стойностите на индикаторал 1,2 , при които са възможни ненулеви стойности за Аи брешения на уравнение (4.6). Тези стойности са

.(4.8)

Ако радикалният израз е отрицателен, тогавал 1,2 комплексно спрегнати числа. Да приемем, че и двата корена на уравнение (4.7) имат ненулеви реални части и че няма кратни корени. Тогава общото решение на системата (4.4) може да бъде представено като линейна комбинация от експоненти с експонентил 1 , л 2 :

(4.9)

За да анализираме естеството на възможните траектории на системата във фазовата равнина, използваме линейна хомогенна координатна трансформация,което ще доведе системата до канонична форма:

,(4.10)

което позволява по-удобно представяне на фазовата равнина в сравнение с оригиналната система (4.4). Да въведем нови координатиξ , η по формулите:

(4.1)

От курса на линейната алгебра е известно, че ако реалните части не са равни на нулал 1 , л 2 оригиналната система (4.4) с помощта на трансформации (4.11) винаги може да бъде трансформирана в каноничната форма (4.10) и нейното поведение във фазовата равнина може да бъде изследваноξ , η . Помислете за различните случаи, които могат да се представят тук.

Корени λ 1 , λ 2 – валидни и със същия знак

В този случай коефициентите на трансформация са реални, ние се движим от реалната равнинаx,yкъм реалната равнина ξ, η. Разделяйки второто от уравненията (4.10) на първото, получаваме:

.(4.12)

Интегрирайки това уравнение, намираме:

Къде .(4.13)

Нека се съгласим да разбираме под λ 2 коренът на характеристичното уравнение с голям модул, което не нарушава общността на нашите разсъждения. Тогава, тъй като в разглеждания случай корените λ 1 , λ2 – валидни и със същия знак,а>1 , и имаме работа с интегрални криви от параболичен тип.

Всички интегрални криви (с изключение на оста η , което съответства на ) докоснете в началото на оста ξ, която също е интегрална крива на уравнение (4.11). Началото на координатите е особена точка.

Нека сега намерим посоката на движение на представителната точка по фазовите траектории. Ако λ 1, λ 2 са отрицателни, тогава, както се вижда от уравнения (4.10), |ξ|, |η| намаляват с времето. Представящата точка се доближава до началото, но никога не го достига. В противен случай това би противоречило на теоремата на Коши, която гласи, че само една фазова траектория минава през всяка точка от фазовата равнина.

Такава сингулярна точка, през която минават интегрални криви, точно като семейство от параболи преминава през началото, се нарича възел (фиг. 4.5)

Равновесно състояние от тип възел при λ 1, λ 2 < 0 е стабилен според Ляпунов, тъй като представителната точка се движи по всички интегрални криви към началото на координатите. то стабилен възел. Ако λ 1, λ 2 > 0, тогава |ξ|, |η| нараства с времето и представителната точка се отдалечава от началото. В този случай сингулярната точка– нестабилен възел .

На фазовата равнина x, y общият качествен характер на поведението на интегралните криви ще се запази, но допирателните към интегралните криви няма да съвпадат с координатните оси. Ъгълът на наклона на тези допирателни ще се определя от съотношението на коефициентите α , β , γ , δ в уравнения (4.11).

Корени λ 1 , λ 2 са валидни и имат различни знаци.

Конвертиране откоординати x,y към координати ξ, η пак истински. Уравненията за каноничните променливи отново имат формата (4.10), но вече знаците λ 1, λ 2 различно. Уравнението на фазовата траектория има формата:

Където ,(4.14)

Интегрирайки (4.14), намираме

(4.15)

то уравнението дефинира семейство от криви от хиперболичен тип, където и двете координатни осиса асимптотите (при а=1 ще имаме семейство от равнобедрени хиперболи). Координатните оси също са интегрални криви в този случай– това ще бъдат единствените интегрални криви, минаващи през началото. всекиот които се състои от три фазови траектории: на две движения към състояние на равновесие (или от състояние на равновесие) и от състояние на равновесие. Всички други интегрални криви– са хиперболи, които не минават през началото (фиг. 4.6) Тази особена точка се нарича "седло ». Линиите на нивото в близост до планинската седловина се държат като фазови траектории в близост до седловината.

Нека разгледаме природата на движението на представителната точка по фазови траектории близо до равновесното състояние. нека напримерλ 1 >0 , λ 2<0 . Тогава представителната точка, поставена върху оста ξ , ще се отдалечи от началото и ще се постави върху оста η – ще се приближава за неопределено време до началото на координатите, без да го достигне за крайно време. Където и да е представящата точка в началния момент (с изключение на сингулярната точка и точките на асимптотата η =0), в крайна сметка ще се отдалечи от равновесното състояние, дори ако в началото се движи по една от интегралните криви към особена точка.

Очевидно е, че седловидна особена точка винаги е нестабилна . Само при специално избрани начални условия на асимптотоη =0 системата ще се приближи до състояние на равновесие. Това обаче не противоречи на твърдението, че системата е нестабилна. Ако броите, че всички начални състояния на системата на фазовата равнина са еднакво вероятни, тогава вероятността за такова начално състояние, което съответства на движение в посокатада се особена точка е равна на нула. Следователно всяко реално движение ще изведе системата от състоянието на равновесие.Връщам се към координатитеx,y,получаваме същата качествена картина за характера на движението на траекториите около началото.

Границата между разглежданите случаи на възел и седло е случаяткога един от характерните показатели, напр λ 1 , изчезва, което се случва, когато детерминантата на системата- израз adbc=0(виж формула 4.8 ). В този случай коефициентите на десните части на уравнения (4.4) са пропорционални един на друг:

и системата има за свои равновесни състояния всички точки на правата:

Останалите интегрални криви са семейство от успоредни прави с наклон , по които представителните точки или се приближават до равновесното състояние, или се отдалечават от него, в зависимост от знака на втория корен на характеристичното уравнение λ 2 = a+d.(фиг.4.7 ) В този случай координатите на равновесното състояние зависят от началната стойност на променливите.

Корени λ 1 , λ 2 – комплексконюгат

В случая наистинахи гние ще имат сложни конюгати ξ , η (4.10) . Въпреки това, чрез въвеждане на още една междинна трансформация, в този случай също е възможно да се намали разглеждането до истинска линейна хомогенна трансформация. Да сложим:

(4.16)

където а, б,и u, v – реални стойности. Може да се покаже, че трансформацията отx,yда се u, v е, според нашите допускания, реален, линеен, хомогенен с ненулев детерминант. Поради уравненията(4.10, 4.16) имаме:

където

(4.17)

Разделяне на второто от уравненията на първото, получаваме:

което е по-лесно за интегриране, ако преминем към полярната координатна система (r, φ ) . След смянаполучаваме откъде:

.(4.18)

По този начин, на фазовата равнинаu, vимаме работа със семейство логаритмични спирали, всяка от които имаасимптотична точка в началото.Особена точка, която е асимптотичната точка на всички интегрални криви, имащи формата на спирали, вложен приятелприятел, обади се фокус ( фиг.4.8 ) .

Нека разгледаме характера на движението на изобразяващата точка по фазовите траектории. Умножавайки първото от уравненията (4.17) поu, а вторият до vи добавяйки, получаваме:

Където

Позволявам а 1 < 0 (а 1 = Reλ ) . След това представящата точка непрекъснато се приближава до началото, без да го достига за крайно време. Това означава, че фазовите траектории са усукани спирали и съответстват на затихнали трептенияпроменливи. То - стабилен фокус .

В случай на стабилен фокус, както и в случай на стабилен възел, е изпълнено не само условието на Ляпунов, но и по-строго изискване. А именно, за всякакви първоначални отклонения, системата в крайна сметка ще се върне възможно най-близо до желаното положение на равновесие. Такава устойчивост, при която първоначалните отклонения не само не нарастват, но намаляват, клонейки към нула, се нарича абсолютна стабилност .

Ако във формулата (4.18) а 1 >0 , тогава представящата точка се отдалечава от началото и имаме работа с нестабилен фокус . При движение от самолетu, vкъм фазовата равнинах, гспиралите също ще си останат спирали, но ще се деформират.

Помислете сега за случая, когатоа 1 =0 . Фазови траектории на самолетаu, vще има кръгове които в самолетаx,yподходящи елипси:

По този начин, приа 1=0 през специална точкаx= 0,y= 0 не преминава интегрална крива. Такава изолирана особена точка, близо до която интегралните криви са затворени криви, по-специално елипси, вградени една в друга и обхващащи особената точка, се нарича център.

По този начин са възможни шест вида равновесно състояние в зависимост от естеството на корените на характеристичното уравнение (4.7). Изглед на фазовите траектории в самолета x, yза тези шест случая е показано на фиг. 4.9.

Ориз. 4.9.Видове фазови портрети в близост до стационарно състояние за системата от линейни уравнения (4.4).

Петте вида равновесни състояния са груби, тяхната природа не се променя с достатъчно малки промени в дясната страна на уравненията (4.4). В този случай промените трябва да са малки не само в десните части, но и в техните производни от първи ред. Шестото състояние на равновесие - центърът - не е грубо. При малки промени в параметрите на дясната страна на уравненията, тя преминава в стабилен или нестабилен фокус.

Бифуркационна диаграма

Нека въведем обозначението:

. (4.11)

Тогава характеристичното уравнение може да бъде написано във формата:

. (4.12)

Помислете за равнина с правоъгълни декартови координати с , д и маркирайте върху него областите, съответстващи на един или друг вид равновесно състояние, което се определя от характера на корените на характеристичното уравнение

.(4.13)

Условието за устойчивост на равновесното състояние ще бъде наличието на отрицателна реална част от yл 1 и л 2 . Необходимо и достатъчно условие за това е изпълнението на неравенстватас > 0, д > 0 . На диаграмата (4.15) това условие съответства на точките, разположени в първата четвърт на равнината на параметрите. Особената точка ще бъде фокусът акол 1 и л 2 комплекс. Това условие съответства на онези точки от равнината, за които , тези. точки между два клона на параболас 2 = 4 д. Точки на полуос с = 0, д>0, съответстват на равновесни състояния от типа център. по същия начин,л 1 и л 2 - валидни, но различни знаци, т.е. особена точка ще бъде седло, ако д<0, и т.н. В резултат на това получаваме диаграма на разделяне на равнината на параметрите с, д, в области, съответстващи на различни видове равновесни състояния.

Ориз. 4.10.Бифуркационна диаграма

за системата от линейни уравнения 4.4

Ако коефициентите на линейната система a, b, c, dзависят от някакъв параметър, тогава когато този параметър се промени, стойностите също ще се променятс , д . При преминаване през границите характерът на фазовия портрет се променя качествено. Следователно такива граници се наричат ​​бифуркационни граници – от противоположните страни на границата системата има два топологично различни фазови портрета и съответно два различни типа поведение.

Диаграмата показва как могат да се случат такива промени. Ако изключим специални случаи - произхода на координатите - тогава е лесно да се види, че седлото може да влезе във възел, стабилен или нестабилен при пресичане на оста y. Стабилният възел може или да се премести в седло, или в стабилен фокус и т.н. Обърнете внимание, че преходите стабилен възел – стабилен фокус и нестабилен възел – нестабилен фокус не са бифуркационни, тъй като топологията на фазовото пространство не се променя в този случай. Ще говорим по-подробно за топологията на фазовото пространство и бифуркационните преходи в Лекция 6.

При бифуркационни преходи естеството на стабилността на сингулярната точка се променя. Например, стабилен фокус през центъра може да се превърне в нестабилен фокус. Тази бифуркация се нарича Бифуркация на Андронов-Хопфпо имената на учените, които са го изследвали. С тази бифуркация в нелинейните системи се ражда граничен цикъл и системата става самоосцилираща (вижте лекция 8).

Пример. Система от линейни химични реакции

вещество хвлива се отвън с постоянна скорост, превръща се във вещество Y и със скорост, пропорционална на концентрацията на веществото Y, се изважда от реакционната сфера. Всички реакции са от първи ред, с изключение на притока на материя отвън, който има нулев ред. Реакционната схема изглежда така:

(4.14)

и се описва със системата от уравнения:

(4.15)

Получаваме стационарни концентрации, като приравняваме десните страни на нула:

.(4.16)

Разгледайте фазовия портрет на системата. Нека разделим второто уравнение на системата (4.16) на първото. Получаваме:

.(4.17)

Уравнение (4.17) определя поведението на променливите във фазовата равнина. Нека изградим фазов портрет на тази система. Първо начертаваме основните изоклини на фазовата равнина. Уравнение на изоклина на вертикални допирателни:

Уравнение за изоклина на хоризонталните допирателни:

Особената точка (стационарно състояние) се намира в пресечната точка на главните изоклини.

Сега нека определим под какъв ъгъл координатните оси пресичат интегралните криви.

Ако x= 0, тогава .

По този начин, допирателната на наклона на допирателната към интегралните криви y=y(x),пресичане на оста y х=0, е отрицателна в горната полуравнина (припомнете си, че променливите x, yимат стойности на концентрация и следователно се интересуваме само от горния десен квадрант на фазовата равнина). В този случай стойността на тангенса на ъгъла на наклона на допирателната се увеличава с разстоянието от началото.

Помислете за оста y= 0. В пресечната точка на тази ос интегралните криви се описват от уравнението

При тангенсът на наклона на интегралните криви, пресичащи абсцисната ос, е положителен и нараства от нула до безкрайност с увеличаване х.

В .

След това, с по-нататъшно увеличение, тангенсът на наклона намалява по абсолютна стойност, оставайки отрицателен и клони към -1 при х ® ¥ . Познавайки посоката на допирателните към интегралните криви на главните изоклини и на координатните оси, е лесно да се изгради цялата картина на фазовите траектории.

Характерът на устойчивостта на сингулярната точка ще бъде установен по метода на Ляпунов. Характеристичната детерминанта на системата има формата:

.

Разширявайки детерминантата, получаваме характеристичното уравнение на системата: , т.е. и двата корена на характеристичното уравнение са отрицателни. Следователно стационарното състояние на системата е стабилен възел. В същото време концентрацията на веществото хклони към стационарно състояние винаги монотонно, концентрацията на веществото Y може да премине през min или max. Осцилаторните режими в такава система са невъзможни.

Позволявам zq - особена точка на функцията f(z), т.с. f(z)но е аналитичен в този момент (по-специално може да не бъде дефиниран в него). Ако съществува такава пунктирана околност на точката zq (т.е. множеството O z - zq f(z) е алиатичен, тогава зоНаречен изолирана сингулярна точкафункции f(z).Това определение също е запазено по делото zn = oo, ако йодът е пробита околност на точка zq = oo разбере комплекта z >аз - появата на някакъв кръг с център в началото. С други думи, сингулярната точка zq се казва, че е изолиран, ако съществува околност на тази точка, в която има други особени точки, различни от zq. Навсякъде по-долу разглеждаме само сингулярни точки с еднозначен характер (функцията f(z)се приема за уникален).

В зависимост от поведението на функцията f(z)при z -> zqИма три вида особени точки. Изолирана особена точка zq функции f(z)Наречен:

1) подвижна особена точкаако има ограничена граница

2) полюсако има ограничение

3) съществен момент,ако f(z) няма нито крайна, нито безкрайна граница за z-> zq.

ПРИМЕР 26.1. Нека покажем, че и трите вида особени точки са реализирани. Обмисли f(z)= точка zq = 0 е изолиран

сингулярна точка на тази функция. Използвайки формула (22.12), получаваме разширението

от което следва, че съществува lim fi(z)= 1. Следователно zq = 0 е

е подвижна особена точка на функцията fi(z).

функция f'j(z) =--- има полюс в точка зо= 1 защото

2 r" Х

Помислете сега за функцията )z(z)= e 1 ^ r и покажете това зо = O е съществена сингулярна точка на тази функция. При стремеж zдо нула по реалната ос, лявата и дясната граница на функцията f (z)различен: лим с 1 / 1 = 0,лим с 1 /* =операционна система. Това предполага,

x->0-0 x->0+O

Какво f:i(z)няма нито крайна, нито безкрайна граница за 2 -> О, т.е. zq = 0 е по същество особена точка на тази функция. (Имайте предвид, че като точка клони z-iyдо нула върху функцията на въображаемата ос

няма никакви ограничения.)

Разбира се, има и неизолирани особени точки. Например. функцията има полюси в точки z n = -, П= ±1, ±2,...

Следователно, Zq = 0 е неизолирана особена точка на тази функция: във всяка (произволно малка) околност на тази точка има други особени точки личен лекар.

Позволявам зо-крайна изолирана сингулярна точка на функция f(z).Тогава f(z)е подобно в някои пунктирани квартали 0 Zo на точката зотази околност може да се разглежда като пръстен с вътрешен радиус r = 0. Съгласно теорема 25.1 в разглежданата околност функцията f(z)може да се разшири в серия на Лоран (25.2). Ще покажем, че поведението на функцията за 2 -> zq (т.е. типът на особената точка зо)зависи от формата на основната част от разлагането (25.2); това обстоятелство обяснява произхода на термина „основна част”.

ТЕОРЕМА 2G.2. Изолирана особена точка zo на функция f(z) е отстранима тогава и само ако разширението на Lorap в пунктиран околност на тази точка има оид

тези. се състои само от правилната част, и всички коефициенти на основната част са равни на куршума.

Доказателство. 1. Нека зое подвижна особена точка. Нека докажем, че разширението на Лоран на функцията f(z)има формата (26.1). От сингулярната точка зоотстраним, тогава има ограничен лимит f(z) = A.Следователно, f(z)ограничена в някаква пунктирана околност 0 z - zq на точката зо,тези. )(z) за всички zот този квартал. Вземете всякакви Р. U р /?|, и използвайте формулите (25.3) за коефициентите на редовете на Лоран:

За коефициентите на основната част на разширението n =- 1,-2,... За такива стойности Пние имаме p~n-е 0 при Р-> 0. Тъй като стойността Рможе да бъде избран произволно малък, тогава г-н~"може да бъде произволно малък. Тъй като |c t,| ^ Mr~nи cn не зависят от p, тогава cn = 0 за и= - 1, -2,..., което трябваше да се докаже.

2. Нека сега приемем, че разширението на Лоран има формата (26.1). Редица (26.1) е степенна редица и. следователно се събира не само в пробития, но и в целия квартал z-zq включително точката зо;неговата сума S(z)е аналитичен за z и S(z) = )(z)при 0 z - зоР.Следователно има краен лимит )(z)\u003d Pm 5 (r) \u003d 5 (r) - Следователно, особената точка zq

Z->Zo Z-*Zo

разполагаем. Теоремата е доказана.

Коментирайте. От доказателството на теоремата следва, че в пунктиран квартал 0 z - zo на подвижна особена точка функцията f(z)съвпада с функцията S(r), която е аналитична в цялата околност z - зо . Следователно, ако поставим /(th) = S(zq), след това, без да променяте стойностите на функцията f(z)във всяка точка от пунктирания квартал, ние правим тази функция аналитична в r, т.е. „премахнете“ функцията. Това обяснява термина „отстранима сингулярност“. Естествено е такива точки да се разглеждат като правилни, а не като особени точки на функцията f(z).

Помислете например за функцията

В пример 26.1 беше показано, че Pm (n) = 1. т.е. сингулярна точка

zq = 0 е отстраним. Задавайки /i(0) = 1, ние по този начин елиминираме сингулярността и получаваме функция, която е аналитична в точката zq = 0 (и в цялата равнина C).

Нека сега характеризираме полюсите от гледна точка на разширенията на Лоран.

Теорема 26.3. Изолирана особена точка Zo на функция f(z) е полюс тогава и само ако, когато главната част от разширението на Лоран с център Zq има само краен брой различни

от нула коефициенти с n:

Доказателство. 1. Нека zq - полюс, т.е. лим /( z) = оо.

Нека докажем, че разширението на Лоран на функцията f(z)има формата (2G.2). Тъй като лим f(z)= оо. тогава съществува пунктирана околност на точката

ki zq. при което f(z)е аналитичен и няма нули. След това функцията g(z) = 1 /f(z)също ще бъде аналитичен в този пробит квартал и лим g(z)= 0. Следователно, Зое за еднократна употреба *-? *0

особена точка на функцията g(z).Нека предефинираме g(z)в точката зо, поставяне g(zo)= 0. Тогава g(z)става аналитичен в цялата околност на (непробитата) точка z 0,и z0ще бъде неговата изолирана нула. Означаваме с нкратност (ред) на тази нула. Както беше показано в §23, в съседство на точката zq функция g(z)представим във формата (виж (23.2))

и (z$) f 0 и y>(z)е аналитично в някаква околност на точката зо-защото ip(z)непрекъснато в точка зои g>(zo) F 0" тогава ip(z)също няма нули в някаква околност на тази точка. Следователно функция 1 /-p(z)също ще бъде аналитичен в този квартал и следователно се разширява в него в серия на Тейлър:

Отваряйки скобите и променяйки обозначенията на коефициентите, записваме последното разширение във формата

където c_jv = 1>o f 0. Така основната част от разширението на Лоран на f(r) съдържа само краен брой членове; стигнахме до търсеното равенство (26.2).

2. Пуснете в пунктирана околност на точка thфункция )(z)е представено от разширението на Лоран (26.2) (в по-разширена форма, вижте (26.3)), чиято основна част съдържа само краен брой членове, и с-д" f 0. Трябва да докажем това Zq - функционален полюс f(z).Умножавайки равенство (26.3) по (Г - Ж o) iV , получаваме функцията

Редът в (26.4) е степенен ред, сходен към аналитична функция не само в пунктираната, но и в цялата околност на точката Zq. Следователно функцията h(z)става аналитичен в този квартал, ако го разширим в th чрез настройка h(zo)= s_dg f 0. Тогава

Така точката o е полюс и теорема 26.3 е доказана.

Кратност (ред) на нулевата функция g(z)= 1//(r) се извиква полюс редфункция /(r). Ако Н-редът на полюса е th, тогава g(z)= (r - Zo)N ip(z),и (върви) Е 0 и както е показано в първата част от доказателството на теорема 26.3, разширението на f(r) има формата (26.3), където c_/v f 0. Обратно, ако f(r) се разшири в редица (26.3) и e-z F 0, тогава

т.с. Н-редът на полюса на функцията f(r). По този начин, редът на zq полюса на функцията/(G) е равно на числото на водещия ненулев коефициент на основната част от разширението на Лоран в пунктираната околност на точката zq(т.е. равно на такова число Н,какво s_dg f 0 и sp= 0 при П > Н).

Нека докажем следното твърдение, което е удобно) за приложения.

Следствие 26.4. Точката zq е полюс от ред N на фикцията/(G) ако и само ако/(G) представят във формата

където h(z) е аналитична функция в околност на точка th и h(zo) f 0.

Доказателство. функция cp(z) = l/h(z)е аналитично в някаква околност на точка r. Условието на следствие 26.4 е еквивалентно на следното:

Ето защо zq - кратност нула нфункции g(z).а оттам и полюса на множествеността нфункции /(2).

II пример 26.5. Намерете изолирани особени точки на функция и определя техния вид.

Намаление Точките, в които (з 2 + 1 )(z+ H) 2 = 0. Ако z 2 Л- 1 = 0, след това 2 = ±rако (з 4- H) 2 = 0, тогава z= -3. Следователно функцията има три особени точки z= r, 22 = -r, З3 = - 3. Помислете z:

G -полюс от първи ред (използвахме следствие 26.4). По подобен начин може да се докаже, че 22 = -исъщо полюс от първи ред. За 2 часа имаме:

Нека преминем към разглеждането на по същество особени точки.

Теорема 26.6. Изолирана особена точка zq на функция f(z) е по същество особена тогава и само ако основната част от разширението на Лоран с център zq има безкрайно много различни от. нула, коефициенти с p.

Доказателство. Теорема 26.6 следва директно от теореми 26.2 и 26.3. Наистина, ако точката zq е по същество единично, тогава основната част от разширението на Лоран не може да отсъства или да съдържа краен брой членове (в противен случай точката Zq ще бъде или подвижен, или стълб). Следователно броят на членовете в основната част трябва да бъде безкраен.

Обратно, ако главната част съдържа безкрайно много членове, тогава Zq не може да бъде нито подвижна точка, нито полюс. Следователно тази точка е по същество единствена.

Съгласно дефиницията една по същество сингулярна точка се характеризира с факта, че функцията f(2) няма нито краен, нито безкраен предел за z ->zq. По-пълна представа за това колко неправилно е поведението на дадена функция в околност на по същество особена точка се дава от следната теорема.

Теорема 26.7 (теорема на Сохоцки). Ако zq е по същество сингулярен, тогава точката на функцията f(z), тогава за всяко комплексно числол, включително A =оо, има последователност от точки z n, така че z n -> zo илим f(zn) = НО.

n->os

Доказателство. Първо разгледайте случая А =оо. В първата част от доказателството на теорема 2G.2 установихме, че ако f(z)е ограничено в някаква пробита околност на точката r0, тогава всички коефициенти c, n = - 1, - 2,... от основната част са равни на нула (и следователно сингулярността в th е отстранима). Тъй като по предположение r0 е по същество особена точка, функцията f(r) е неограничена във всяка пунктирана околност на точката r0. Нека вземем някакъв тесен квартал 0 Z, така че f(zi) > 1 (ако |/(r)| z - zo R/2 има точка z-2 , където |/(dd)| > 2 и т.н.: в пунктирания квартал О 71. Очевидно е, че rn -e go и lim /(r«) = оо. Така, в случай A = oo, теорема 26.7

доказано.

Нека сега A fоо. Да приемем първо, че има пробита околия 0

= -yy---- ще бъде аналитичен в този прободен квартал и следователно,

/(G) - НО

следователно r е изолирана сингулярна точка на функцията Φ(r). Нека покажем. че r0 е по същество особена точка на Φ(r). Нека да е грешно. Тогава съществува граница lim Φ(r), крайна или безкрайна. защото

/(r) = A + , тогава Hsh /(r) също съществува, което противоречи на условието

F(g) ~ :-*z 0

изглед на теоремата. Така r0 е по същество особена точка на функцията Φ(r). Съгласно доказаното по-горе, съществува последователност от точки r n такава, че r n o и lim Φ(r n) = oo. Оттук

Ние доказахме изискваното твърдение при предположението, че f(r) Ф Ав някаква пунктирана околност на точката r. Нека сега приемем, че това не е вярно, т.е. във всяка произволно малка пунктирана околност на точката th има такава точка G",че f(r") = A. Тогава за всяко Пв пунктираната околност 0 f(z u) = L. Следователно изискваното твърдение е вярно П-юо

във всички случаи и теорема 26.7 е доказана.

Съгласно теорема 26.7 (на Сохотски), във всяка (произволно малка) пунктирана околност на по същество особена точка функцията f(r) приема стойности произволно близки до произволно число в разширената комплексна равнина C.

За изучаване на изолирани особени точки често са полезни добре познатите разширения на Тейлър на основни елементарни функции.

ПРИМЕР 2G.8. Определете вида на особената точка zq = 0 за функцията

Решено и д. Развиваме числителя и знаменателя в ред на Тейлър по степени на r. Заместваме в (22.11) 3 zвместо r и изваждане на 1, получаваме

Използвайки (22.12), получаваме разширението на знаменателя:

Сериите в тези разширения се събират в цялата комплексна равнина €. Ние имаме

и /2(2) са аналогични в околност на точката зо = 0 (и дори в цялата равнина) и /2(20) Е 0, тогава h(z)също е аналитична в някаква околност на точката gF 0. Съгласно следствие 26.4 точката Zo = 0 е полюсът на реда N = 4.

II пример 26.9. Намиране на особени точки на функция f(z)= sin j - и определете вида им.

P e в e и e. Функцията има една единствена крайна особена точка zq = 1. В други точки от C функцията w =--- аналитичен; следователно функцията грях wще бъде аналитичен.

Замествайки в разширяването на синуса (22.12) - вместо r, получаваме

Получихме разширението на функцията sin в редица на Лоран в пунктирана околност на точката 20 = 1. Тъй като полученото разширение съдържа безкрайно много членове с отрицателни степени (r - 1), тогава zq = 1 е съществена сингулярна точка (в този случай разширението на Лоран се състои само от основната част и правилната част липсва).

Обърнете внимание, че в този случай също беше възможно да се установи природата на сингулярността директно от дефиницията, без да се прибягва до разширяване на серията. Наистина има последователности (r") и (2"), които се събират към зо= 1 и така че f(z" n)= 1, /(2") = 0 (посочете сами такива последователности). Така че, f(z)няма ограничение кога z -> 1 и оттук точката zq - 1 е по същество единствено число.

Нека въведем концепцията за разширение на Лоран на функция в околност на точка Zq = 00 и разгледайте връзката между разширението и природата на сингулярността в тази точка. Обърнете внимание, че дефинициите на изолирана сингулярна точка и нейния тип (отстраняема, полюсна или по същество сингулярна) се пренасят в случая zq = oc непроменен. Но теореми 26.2. 26.3 и 26.6, свързани с природата на разширенията на Лоран, трябва да бъдат променени. Въпросът е, че членовете c n (z - 2o) стр. П= -1,-2,..., основната част, определяща "неправилността" на функцията близо до крайната точка Zq, тъй като 2 клони към oo, те ще се държат „правилно“ (клонят към 0). Напротив, членовете на редовната част с П= 1,2,... ще клони към oo; те определят природата на сингулярността в Zq = oo. Следователно основната част от разширението в околностите на oo ще бъдат термините с положителни мощности П,и правилно - с отрицателна.

Нека въведем нова променлива w = 12. функция тв= 1/2, разширена така, че u(oo) = 0, едно към едно и конформно картографира околността z > Rточки zq = 00 в околността на |w| wq = 0. Ако функцията f(z)анализи в пробит квартал Р z Zq = oc, тогава функцията G(w) = f(l/w)ще бъде аналитично в жълтия квартал 0 wo = 0. Тъй като за 2 -> oo ще има w-> 0, тогава

Ето защо G(w)има в точката wq = 0 е сингулярност от същия тип като f(z)в точката Zq = 00. Нека разширим функцията G(w) в серия на Лоран в пунктирана околност на точката wo = 0:

Сумите от дясната страна на (26.5) представляват съответно правилната и основната част на разширението. Да преминем към променливата z,заместване w = 1/z:

обозначаващ П\u003d -A *, 6 * \u003d 6_ " \u003d с пи забелязвайки това G(l/z) = f(z), получаваме

Разлагането (2G.G) се нарича Разложение на Лоран на функцията f(z) в пунктирана околност на точката zq= оо. Първата сума в (2G.6) се нарича дясна част, а втората сума е Главна часттова разлагане. Тъй като тези суми съответстват на правилните и главни части на разширението (26.5), разширението (26.6) удовлетворява аналозите на теореми 26.2, 26.3 и 26.6. Така следната теорема е аналог на теорема 26.2.

Теорема 26.10. Изолирана особена точкаZq - операционна система (функции/(G) е отстраним ако и само ако разширението на Лоран в прободен квартал на тази точка има формата

т.с. се състои само от правилната част.

Поставяме /(oo) = ко.Функцията, дефинирана от редицата (26.7), събираща се в околността z > Rточки 2o \u003d oc, наречени аналитично в точка zо = оо. (Имайте предвид, че тази дефиниция е еквивалентна на аналитичността на функцията G(w) в точката горе = 0.)

Пример 26.11. Изследвайте сингулярната точка zq = oo на функцията

Тъй като границата е крайна, тогава зо = oo е подвижна особена точка на функцията f(r). Ако поставим /(oo) = lim Джей Зи)= 0, тогава f(z)ще стане

тик в точката Зо= ос. Нека покажем как да намерим съответното разширение (26.7). Да преминем към променливата w = 1 fz.Заместване z= 1 /?e, получаваме

(последното равенство е валидно в пунктираната околност на точката ww = 0, но ние ще разширим определението (7(0) = 0). Получената функция има особени точки w =±i, w =-1/3, и в точката Wq = 0 е аналитично. Функция за разширяване G(w)по степени w(както беше направено в пример 25.7) и заместване в получената степенна серия w = 1/zможе да се получи разширението (26.7) на функцията f(z).

Теорема 26.3 за случая зо= oo ще бъде пренаписано в следната форма.

Теорема 26.12. Изолирана особена точкаотивам = ок функция f(z) е полюс тогава и само ако главната част от разширението на Лоран (26.6) има само краен брой ненулеви коефициентиС":

Тук серията е правилната част, а полиномът в скоби е основната част от разширението. Множеството на полюса в oc се определя като множеството на полюса wq = 0 функции G(z).Лесно се вижда, че кратността на полюса съвпада с числото нв (26.8).

Q p | (i 2 + 1) (z + 3) 2

Задача. Покажете, че функцията f(z) =-- -- има в

точка зо = oo ред на стълбове 3.

Теорема 26.6 за съществена особена точка е пренаписана за случая зо= os почти дословно и не се спираме подробно на него.

Основни понятия и определения:

Нулата на аналитичната функция f(z) е точката „a“, за която f(a)=0.

Нулата от ред “n” на функцията f(z) е точката “a”, ако не е fn(a)¹0.

Особена точка "a" се нарича изолирана особена точка на функцията f(z), ако съществува околност на тази точка, където няма особени точки, различни от "a".

Изолираните особени точки биват три вида: .

1 подвижни специални точки;

3 съществени сингулярни точки.

Видът на особена точка може да се определи въз основа на поведението на дадената функция в намерената особена точка, както и от формата на реда на Лоран, получен за функцията в околността на намерената особена точка.

Определяне вида на особена точка по поведението на функцията в нея.

1. Премахваеми особени точки.

Изолирана особена точка a на функцията f(z) се нарича отстранима, ако съществува крайна граница.

2. поляци.

Изолирана особена точка a на функцията f(z) се нарича полюс, ако .

3. Значими особени точки.

Изолирана особена точка a на функция f(z) се нарича съществена особена точка, ако не съществува нито крайна, нито безкрайна.

Между нулите и полюсите на функцията има следната връзка.

За да бъде точка a полюс от порядък n на функцията f(Z), е необходимо и достатъчно тази точка да бъде нула от порядък n за функцията .

Ако n=1 полюсът се нарича прост.

определение:Изолирана особена точка на еднозначен знак се нарича:

а) отстраним, ако основната част от разлагането отсъства;

б) полюс, ако основната част съдържа краен брой членове;

в) по същество особена точка, ако основната част съдържа безкраен брой членове.

а) По този начин, в съседство на подвижна особена точка, разширението има формата:

той изразява функцията във всички точки на окръжността |z-a|

В центъра z=a равенството е невярно, защото функцията при z=a има прекъсване, а дясната страна е непрекъсната. Ако стойността на функцията в центъра се промени, като се вземе равна на стойността от дясната страна, тогава празнината ще бъде елиминирана - оттук и името - сменяема.

b) В близост до полюс от порядък m, разширението на реда на Лоран има формата:

в) В близост до обикновен стълб

Удръжки и формули за тяхното изчисляване.

Остатъкът на аналитична функция f(z) в изолирана особена точка z 0 е комплексно число, равно на стойността на интеграла , взети в положителна посока по окръжността L с център в точката z 0 , която се намира в областта на аналитичност на функцията f(z) (т.е. в пръстена 0<|z-z0|

Остатъкът на функцията f(z) в изолирана особена точка z 0 се обозначава със символа Res f(z 0) или Res (f(z); z 0). По този начин,

Resf(z0)= . (22.15.1)

Ако поставим n=-1 във формулата (22.15.1), тогава получаваме:

C-1=

или Res f(z 0)= C -1,

тези. остатъкът на функцията f(z) по отношение на особената точка z 0 е равен на коефициента на първия член с отрицателен показател в разлагането на функцията f(z) в редица на Лоран.

Изчисляване на удръжки.

Правилни или подвижни особени точки. Очевидно, ако z=z 0 е правилна или отстранима особена точка на функцията f(z), тогава Res f(z 0)=0 (в тези случаи няма главна част в разлагането на Лоран, така че c-1= 0).

поляк. Нека точката z 0 е прост полюс на функцията f(z). Тогава редът на Лоран за функцията f(z) в околност на точката z 0 има формата:

Оттук

Следователно, преминавайки в това равенство до границата като z --z 0 , получаваме

Res f(z0)=

По същество специална точка. Ако точката z 0 е по същество особена точка на функцията f(z), тогава за да се изчисли остатъкът на функцията в тази точка, обикновено се определя директно коефициентът c-1 в разширението на функцията в редица на Лоран.

Класификация на събитията. Сума, произведение на събитията, техните свойства, графично представяне.

Събитията са разделени на:

1. Случаен

2. Достоверен

3. Невъзможно

Надеждно - това е събитие, което задължително се случва в тези условия (нощта е последвана от сутрин).

Случайно е събитие, което може или не може да се случи (полагане на изпит).

Невъзможното е събитие, което няма да се случи при дадените условия (извадете зелен молив от кутията само с червени).

сингулярна точка

по математика.

1) Особена точка на кривата, дадена от уравнението F ( x, y) = 0, - точка M 0 ( x 0, y 0), в която и двете частни производни на функцията F ( x, y) изчезват:

Ако в допълнение не всички втори частични производни на функцията F ( x, y) в точката M 0 са равни на нула, тогава O. t. се нарича двойно. Ако заедно с изчезването на първите производни в точката M 0 всички втори производни изчезнат, но не всички трети производни са равни на нула, тогава O. t. се нарича троен и т.н. При изучаване на структурата на крива в близост до двойно O. t., важна роля играе знакът на израза

Ако Δ > 0, тогава О. т. се нарича изолиран; например кривата y 2 - x 4 + 4x 2= 0 произходът е изолиран O. t. (вж ориз. един ). Ако Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - a 4= 0 началото на координатите е възловата O. t. (вж ориз. 2 ). Ако Δ = 0, тогава кривата O. t. е или изолирана, или се характеризира с факта, че различни клонове на кривата имат обща допирателна в тази точка, например: допирателна и образуват точка, като крива y 2 - x 3= 0 (виж ориз. 3 , а); б) куспида от 2-ри вид - различни клонове на кривата са разположени от една и съща страна на общата допирателна, като крива (y - x 2)2 - х 5= 0 (виж ориз. 3 , b); в) точка на самоконтакт (за крива y 2 - x 4= 0 произходът е точка на самодокосване; (см. ориз. 3 , в). Наред с посочените О. т. има много други О. т. със специални имена; например, асимптотична точка е върхът на спирала с безкраен брой навивки (виж фиг. ориз. четири ), точка на прекъсване, ъглова точка и т.н.

2) Особена точка на диференциално уравнение е точка, в която и числителят, и знаменателят на дясната страна на диференциалното уравнение изчезват едновременно (вижте Диференциални уравнения)

където P и Q са непрекъснато диференцируеми функции. Ако приемем, че O. t. се намира в началото на координатите и използвайки формулата на Тейлър (вижте формулата на Тейлър), можем да представим уравнение (1) във формата

където P 1 ( x, y) и Q 1 ( x, y) са безкрайно малки по отношение на

А именно, ако λ 1 ≠ λ 2 и λ 1 λ 2 > 0 или λ 1 = λ 2, тогава O. t. е възел; всички интегрални криви, минаващи през точки от достатъчно малка околност на възела, влизат в него. Ако λ 1 ≠ λ 2 и λ 1 λ 2 i β, α ≠ 0 и β ≠ 0, тогава O. t. е фокус; всички интегрални криви, минаващи през точки в достатъчно малка околност на фокуса, са спирали с безкраен брой навивки във произволно малка околност на фокуса. Ако накрая λ 1,2 = ± азβ, β ≠ 0, тогава характерът на O. t. не се определя от линейните членове в разширенията на P ( x, y) и Q ( x, y), какъвто беше случаят във всички горепосочени случаи; тук O. t. може да бъде фокус или център или може да има по-сложен характер. В близост до центъра всички интегрални криви са затворени и съдържат центъра в себе си. Така, например, точката (0, 0) е възел за уравненията при" = 2u/x(λ 1 = 1, λ 2 = 2; виж ориз. 5 , а) и г" = u/x(λ 1 = λ 2 = 1; виж ориз. 5 , b), седло за уравнението y" = -y/x(λ 1 = -1, λ 2 = 1 ; см. ориз. 6 ), фокусът за уравнението y" =(x + y) / (x - y) (λ 1 = 1 - аз, λ 2 = 1 + аз; см. ориз. 7 ) и центъра на уравнението y" = -x / y(λ 1 = -и, λ 2 = аз; см. ориз. осем ).

Ако x, y) и Q ( x, y) са аналитични, околността на O. t. от по-висок ред може да бъде разделена на области: D 1 - изпълнена с интегрални криви, двата края влизащи в O. t. (елиптични области), D 2 - изпълнена с интегрални криви, единият край влиза в O. t. (параболични области) и D 3 - области, ограничени от две интегрални криви, включени в O. t., между които има интегрални криви от типа на хиперболи (хиперболични области) (виж. ориз. 9 ). Ако няма интегрални криви, влизащи в точка O., тогава точката O. се нарича точка от стабилен тип. Околността на стабилен O. t. се състои от затворени интегрални криви, съдържащи O. t. вътре в себе си, между които са разположени спирали (виж фиг. ориз. десет ).

Изследването на О. т. диференциални уравнения, т.е. по същество изследването на поведението на семейства от интегрални криви в съседство на О. т. М. Ляпунов а, А. Поанкаре и др.).

3) Особена точка на еднозначна аналитична функция е точка, в която е нарушена аналитичността на функцията (вижте Аналитични функции). Ако има квартал на О. т. а, свободен от други O. t., тогава точката асе нарича изолиран О. т. Ако ае изолиран O. t. и съществува краен a се нарича отстраним O. t. f(а)= б, възможно е да се постигне аще стане обикновена точка на коригираната функция. Например точка z= 0 е отстраним O.T. за функцията f 1 ( z) = f(z), ако z≠ 0 и f 1(0),=1, точка z= 0 е обикновена точка [ f 1 (z) е аналитичен в точката z= 0]. Ако а- изолиран О. т. и а се нарича полюс или несъществена особена точка на функцията f(z), ако серията на Лоран) функционира f(z) в съседство на изолиран O. t. не съдържа отрицателни мощности z - a, ако а- отстраним O. t., съдържа краен брой отрицателни мощности z - a, ако а- полюс (в този случай редът на полюса Рсе определя като най-високата степен на a - по същество особена точка. Например за функцията

p = 2, 3, …)

точка z= 0 е полюсът на реда Р, за функцията

точка z= 0 е съществена сингулярна точка.

На границата на окръжността на сходимост на степенен ред трябва да има поне един O. m.от функцията, представена вътре в този кръг от дадения степенен ред. Всички гранични точки на областта на съществуване на еднозначна аналитична функция (естествена граница) са гранични точки на тази функция. Така всички точки от единичната окръжност | z| = 1 са специални за функцията

За многозначна аналитична функция, концепцията за „O. T." по-трудно. В допълнение към O. t., в отделни листове на риманова повърхност на функция (т.е. O. t. на еднозначни аналитични елементи), всяка точка на разклонение също е O. t. на функцията. Изолирани точки на разклонение на риманова повърхност (т.е. точки на разклонение, така че в някои от техните околности няма други функции на O.t. във всеки лист) се класифицират както следва. Ако a е изолирана точка на разклонение с краен ред и съществува ограничено a, тя се нарича критичен полюс. Ако ае изолирана точка на разклонение от безкраен ред и a се нарича трансцендентална O. t. Всички други изолирани точки на разклонение се наричат ​​критични по същество сингулярни точки. Примери: точка z= 0 е обикновена критична точка на функцията f ( z) = дневник zи критична съществена сингулярна точка на функцията f (z) = регистър на грешките z.

Всеки O. t., с изключение на отстраним, е пречка за аналитичното продължение, т.е. аналитичното продължение по крива, минаваща през неотстраним O. t., е невъзможно.

Велика съветска енциклопедия. - М.: Съветска енциклопедия. 1969-1978 .

Вижте какво е "Специална точка" в други речници:

Точки тук. Вижте също особена точка (диференциални уравнения). Характеристика или сингулярност в математиката е точка, в която даден математически обект (обикновено функция) не е дефиниран или има неправилно поведение (например точка, в която ... ... Уикипедия

Аналитична функция е точка, в която условията на аналитичност са нарушени. Ако аналитична функция f(z) е дефинирана в някаква околност на точката z0 навсякъде … Физическа енциклопедия

Аналитична функция е точката, в която аналитичността на функция е нарушена ... Голям енциклопедичен речник

сингулярна точка- — [Я.Н.Лугински, М.С.Фези Жилинская, Ю.С.Кабиров. Английско-руски речник по електротехника и енергетика, Москва, 1999] Теми по електротехника, основни понятия EN singular point ... Наръчник за технически преводач

1) OT на аналитична функция f(z) е пречка за аналитичното продължение на елемент от функцията f(z) на комплексна променлива z по някакъв път в равнината на тази променлива. Нека аналитичната функция f(z) е дефинирана от някои ... ... Математическа енциклопедия

Аналитична функция, точката, в която аналитичността на функцията е нарушена. * * * ОСОБЕНА ТОЧКА ОСОБЕНА ТОЧКА на аналитична функция, точка, в която аналитичността на функцията е нарушена ... енциклопедичен речник

сингулярна точка- ypatingasis taškas statusas T sritis automatika atitikmenys: англ. особена точка vok. единствено число Punkt, м рус. особена точка, fpranc. точкова частица, m; отделна точка, m … Automatikos terminų žodynas

сингулярна точка- ypatingasis taškas statusas T sritis fizika atitikmenys: англ. особена точка vok. единствено число Punkt, м рус. особена точка, fpranc. отделна точка, m … Fizikos terminų žodynas

Сериите на Тейлър служат като ефективен инструмент за изследване на функции, които са аналитични в окръжността zol За да се изследват функции, които са аналитични в пръстеновидна област, се оказва, че е възможно да се конструират разширения в положителни и отрицателни степени (z - zq) на форма, която обобщава разширенията на Тейлър. Серията (1), разбирана като сбор от две серии, се нарича серия на Лоран. Ясно е, че областта на сходимост на редица (1) е общата част от областите на сходимост на всяка от сериите (2). Да я намерим. Областта на сближаване на първата серия е кръг, чийто радиус се определя от формулата на Коши-Адамар Вътре в кръга на сближаване, серия (3) се сближава с аналитична функция и във всеки кръг с по-малък радиус се сближава абсолютно и равномерно. Вторият ред е степенен ред по отношение на променливата. Серията (5) се сближава в рамките на своя кръг на сходимост към аналитичната функция на комплексната променлива m-*oo и във всяка окръжност с по-малък радиус се сближава абсолютно и равномерно, което означава, че областта на сближаване на серията (4) е появата на кръга - Ако тогава има обща област на сближаване на серията (3) и (4) - кръгъл пръстен, в който серията (1) се свежда до аналитична функция. Освен това, във всеки пръстен, той се сближава абсолютно и равномерно. Пример 1. Определяне на областта на сближаване на радовата серия на Лоран. Изолираните сингулярни точки и тяхната класификация (z), която е еднозначна и аполитична в кръгов пръстен, могат да бъдат представени в този пръстен като сума от сходяща серия, чиито коефициенти Cn се определят еднозначно и се изчисляват по формулите, където 7p е окръжност с радиус m. Нека фиксираме произволна точка z вътре в пръстена R Построяваме окръжности с центрове в точката r, чиито радиуси удовлетворяват неравенствата и разглеждаме нов пръстен.Съгласно интегралната теорема на Коши за многосвързана област имаме За всички точки £ по протежение на окръжността 7d* е изпълнена връзката de сумата на равномерно сходящ се ред 1 1. Следователно фракцията ^ може да бъде представена във vi- /" / По малко по-различен начин за всички точки ξ на окръжността ir> имаме отношението Следователно дробта ^ може да бъде представена като сума от равномерно сходящ се ред във формули (10) и (12) са аналитични функции в кръгов пръстен. Следователно, според теоремата на Коши, стойностите на съответните интеграли не се променят, ако кръговете 7/r и 7r/ се заменят с който и да е кръг. Това ни позволява да комбинираме формули (10) и (12). Заменяйки интегралите от дясната страна на формула (8) с техните изрази (9) и (11), съответно, получаваме желаното разширение. Тъй като z е произволно точка на пръстена, следва, че серията ( 14) се свежда към функцията f(z) навсякъде в този пръстен и във всеки пръстен серията се свежда към тази функция абсолютно и равномерно. Нека сега докажем, че разлагането на формата (6) е единствено. Да приемем, че има още едно разлагане.Тогава навсякъде вътре в пръстена R имаме На окръжността редовете (15) се събират равномерно. Умножете двете страни на равенството (където m е фиксирано цяло число и интегрирайте и двете серии член по член. В резултат на това получаваме от лявата страна, а отдясно - Csh. Така, (4, \u003d St. Тъй като m е произволно число, тогава последната серия от равенства (6), чиито коефициенти се изчисляват по формули (7), се нарича серия на Лоран на функцията f(z) в пръстена 7) за коефициентите на серията на Лоран са рядко се използват на практика, тъй като по правило изискват тромави изчисления. Обикновено, ако е възможно, се използват готови разширения на Тейлър на елементарни функции. Въз основа на уникалността на разширението всеки легитимен метод води до същия резултат. Пример 2 Разгледайте разширенията на серията на Лоран на функции от различни области, като приемем, че Fuiscius /(r) има две особени точки: Следователно има три пръстеновидни области и с център в точката r = 0. във всяка от които функцията f(r) е аналитична: а) окръжността е външната страна на окръжността (фиг. 27). Нека намерим разширенията на Лоран на функцията /(z) във всяка от тези области. Представяме /(z) като сума от елементарни дроби а) Окръжност Преобразуване на връзката (16), както следва Използвайки формулата за сумата от членовете на геометрична прогресия, получаваме б) Пръстенът за функцията -z остава конвергентен в този пръстен, тъй като Серия (19) за функцията j^j за |z| > 1 се разминава. Следователно трансформираме функцията /(z) по следния начин: прилагайки отново формула (19), получаваме, че Този ред се сближава за. Замествайки разширенията (18) и (21) във връзка (20), получаваме c) Външността на окръжността за функцията -z с |z| > 2 се разминава и ред (21) за функцията Нека представим функцията /(z) в следната форма: /<*>Използвайки формули (18) и (19), получаваме ИЛИ 1 Този пример показва, че за същата функция f(z) разширението на Лоран, най-общо казано, има различен вид за различни пръстени. Пример 3. Намерете разлагането на 8 реда на Лоран на функцията Серия на Лоран Изолирани особени точки и тяхната класификация в пръстеновидната област A Използваме представянето на функцията f (z) в следната форма: и трансформираме втория член Използвайки формула за сумата от членовете на геометрична прогресия, получаваме Замествайки намерените изрази във формулата (22), имаме Пример 4. Разгънете функцията в серия на Лоран в близост до тънък zq = 0. За всяка сложна , имаме Нека Това разширение е валидно за всяка точка z Ф 0. В този случай пръстеновидната област е цялата комплексна равнина с една изхвърлена точка z - 0. Тази област може да бъде дефинирана чрез следната зависимост: Тази функция е аналитична в областта От формули (13) за коефициентите на редицата на Лоран, чрез същите разсъждения, както в предходния параграф, могат да се получат неравенствата на Куйв. ако функцията f(z) е ограничена в окръжност, където M е константа), тогава изолирани сингулярни точки Точка zo се нарича изолирана сингулярна точка на функцията f(z), ако съществува пръстеновидна околност на точката ( това множество понякога се нарича също пунктирана околност на точката 2o), където функцията f(z) е еднозначна и аналитична. В самата точка zo функцията или не е дефинирана, или не е еднозначна и аналитична. Различават се три вида особени точки в зависимост от поведението на функцията /(z) при приближаване до точката zo. За изолирана особена точка се казва, че е: 1) отстранима, ако съществува ограничена 2) pmusach, ако 3) по същество особена точка, ако функцията f(z) няма ограничение за Теорема 16. Изолирана особена точка z0 на функция f(z) е отстранима особена точка тогава и само ако разширението на Лоран на функцията f(z) в околност на точката zo не съдържа главна част, т.е. има формата Let zo - подвижна особена точка. Тогава съществува крайна функция, следователно функцията f(z) е ограничена в прокологична околност на точката r. Задаваме По силата на неравенствата на Коши Тъй като е възможно да се избере p като произволно малък, тогава всички коефициенти при отрицателните степени (z - 20) са равни на нула: Обратно, нека Лоран разширението на функцията /(r) в околност на точката zq съдържа само правилната част, т.е. има формата (23) и, следователно, е Тейлър. Лесно се вижда, че за z -* z0 функцията /(r) има гранична стойност: Теорема 17. Изолирана особена точка zq на функцията f(z) е отстранима тогава и само ако функцията J(z) е ограничена в някакъв пунктиран квартал на точката zq, Zgmechai не. Нека r0 е отстранима особена точка на f(r). Ако приемем, че получаваме, че функцията f(r) е аналитична в някакъв кръг с център в точката th. Това определя името на точката - еднократна. Теорема 18. Изолирана особена точка zq на функция f(z) е полюс тогава и само ако главната част от разширението на Лоран на функцията f(z) в околност на точката съдържа крайно (и положително) число на ненулеви членове, т.е. има формата 4 Нека z0 е полюс. Оттогава съществува пунктирана околност на точката z0, в която функцията f(z) е аналитична и различна от нула. Тогава аналитична функция е дефинирана в тази околност и следователно точката zq е подвижна особена точка (нула) на функцията или където h(z) е аналитична функция, h(z0) ∩ 0. е аналитична в околност на точката zq и следователно, откъдето получаваме, че Нека сега приемем, че функцията f(z) има разлагане на формата (24) в пунктирана околност на точката zo. Това означава, че в тази близост функцията f(z) е аналитична заедно с функцията. За функцията g(z) е валидно разширението, от което е ясно, че zq е подвижна особена точка на функцията g(z) и съществува. Тогава функцията клони към 0 - полюсът на функцията. Има още една проста факт. Точката Zq е полюс на функцията f(z) тогава и само ако функцията g(z) = y може да бъде разширена до аналитична функция в околност на точката zq чрез задаване на g(z0) = 0. Редът на полюса на функцията f(z) се нарича ред нула на функция jfa. Теореми 16 и 18 предполагат следното твърдение. Теорема 19. Изолирана сингулярна тънка е по същество сингулярна тогава и само ако главната част от разширението на Лоран в пунктирана околност на тази точка съдържа безкрайно много ненулеви членове. Пример 5. Особената точка на функцията е zo = 0. Имаме изолирани особени точки от серията на Лоран и тяхната класификация. Следователно zo = 0 е отстранима особена точка. Развиването на функцията /(z) в редица на Лоран в близост до нулевата точка съдържа само правилната част: Пример7. f(z) = Особената точка на функцията f(z) е zq = 0. Разгледайте поведението на тази функция на реалната и въображаемата ос: на реалната ос при x 0, на въображаемата ос. Следователно, нито крайните, нито безкрайна граница f(z) при z -* 0 не съществува. Следователно точката r0 = 0 е по същество особена точка на функцията f(z). Нека намерим разширението на Лоран на функцията f(z) в околност на нулевата точка. За всеки комплекс С имаме Let. Тогава разширението на Лоран съдържа безкраен брой членове с отрицателни степени на z.