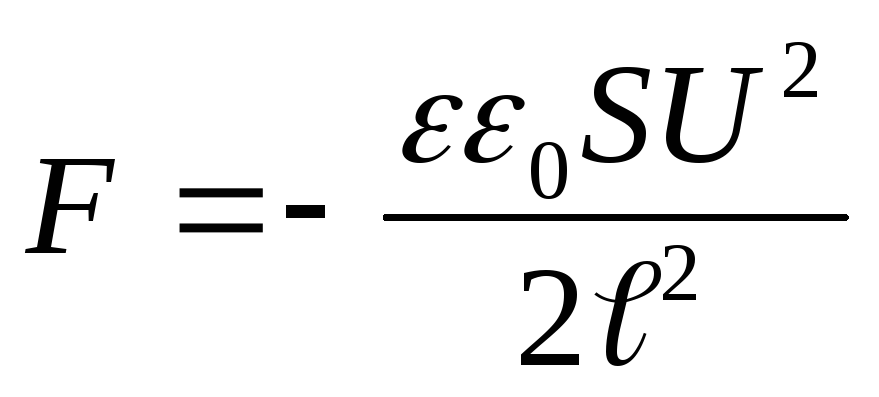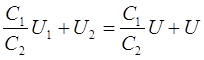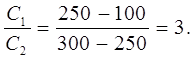Differenza di potenziale totale U0 tra gli elettrodi è
Calcoli:
Risposta: densità di carica superficiale sulle piastre di un condensatore
Problema 23
Area della piastra piatta condensatore ad aria, la distanza tra loro d= 5 mm. Una differenza di potenziale viene applicata alle piastre di un condensatore. Dopo che il condensatore è stato scollegato dalla sorgente di tensione, lo spazio tra le piastre del condensatore viene riempito di ebanite. Quale sarà la differenza potenziale tra i piatti dopo il riempimento? Trova le capacità del condensatore e le densità di carica superficiale sulle piastre prima e dopo il riempimento.
| d
|
| d
|
quindi prima e dopo il riempimento abbiamo
Dato che s=cost e d=cost, noi abbiamo
![]()
Prima e dopo il riempimento con ebanite, abbiamo
![]()
Densità di carica superficiale
Calcoli:
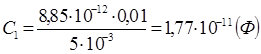
Risposta: prima e dopo il riempimento con ebanite abbiamo
Problema 24
Tra i piatti condensatore piatto, situato a distanza d=1 cm di distanza, differenza di potenziale applicata u\u003d 100 V. Una piastra parallela al piano di bromuro di tallio cristallino () spessa è adiacente a una delle piastre. Dopo aver scollegato il condensatore dalla sorgente di tensione, la lastra di cristallo viene rimossa. Quale sarà la differenza di potenziale tra le piastre del condensatore dopo questo?
possiamo scrivere
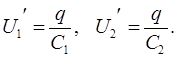
La tensione della batteria sarà uguale alla somma delle tensioni sui singoli condensatori, ovvero
![]()
Di conseguenza,
Pertanto, per la capacità DA di tutta la batteria che troviamo
| DA -q +q d0 e e 01 U 1 |
| ¢ d +q -q e=1 U2 |
Sostituendo (1) in (2), otteniamo
Capacità del condensatore nella seconda posizione
Secondo la legge di conservazione della carica q=q¢, cioè.
Calcoli:
Risposta: la differenza di potenziale diventerà 1,8 kV.
Problema 25
Trova capacità DA il sistema di condensatori mostrato in figura. Capacità di ciascun condensatore DA\u003d 0,5 uF.
| C1 C3 C2 |
trova C ris la batteria di condensatori risultante.
Considera una batteria e un condensatore Da 3, sono collegati in serie. Sapendo che a connessione seriale
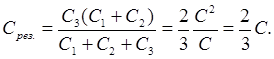
Calcoli:
Risposta: la capacità del sistema di condensatori è uF.
Problema 26
Le capacità di due condensatori sono state confrontate con un elettrometro. Per fare ciò, sono stati addebitati a potenziali differenze U 1=300 V e U2=100 V e collegati entrambi i condensatori in parallelo. La differenza di potenziale misurata in questo caso tra le piastre del condensatore è risultata uguale u\u003d 250 V. Trova il rapporto tra le capacità
| un) C1 + - U 1 |
| b) C2
dove u- differenza di potenziale tra le piastre dopo la loro connessione.
Sostituzione dei valori q 1 , q 2 , q 1 ¢, q 2 ¢ nell'espressione (1), otteniamo dividi per DA 2
Calcoli:
Risposta: rapporto di condensatori Problema 27 Piastre di un condensatore piatto con un'area Sostituisci (2) in (1) ed esprimi q Sostituiamo l'espressione (2) in (4), otteniamo Sostituisci (5) in (6) Calcoli: |
Semestre 3. Lezione4.
Lezione 4. Campo elettrico dei conduttori carichi.
L'energia del campo elettrostatico.
Campo vicino al capotreno. Capacità di conduttori e condensatori. (Capacità di condensatori piatti, cilindrici e sferici). Energia di un sistema di oneri fissi. L'energia di un conduttore carico, condensatore. Densità di energia del campo elettrostatico.
Quando un conduttore viene introdotto in un campo elettrico esterno, le cariche all'interno del conduttore iniziano a muoversi sotto l'azione di forze provenienti dal campo esterno fino al raggiungimento dell'equilibrio. Questo porta ad una ridistribuzione della carica elettrica all'interno del conduttore. Le regioni del conduttore, precedentemente elettricamente neutre, acquisiscono una carica elettrica non compensata. Di conseguenza, un campo elettrico appare (o, come si dice, è indotto) nel conduttore 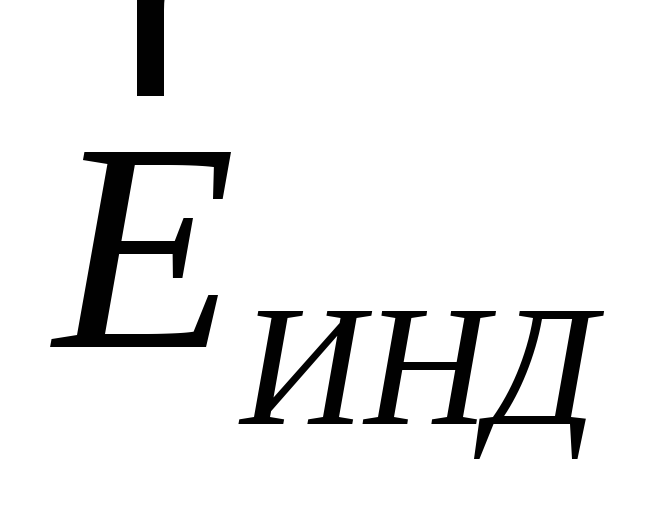 . La condizione per l'equilibrio delle cariche elettriche:
. La condizione per l'equilibrio delle cariche elettriche:
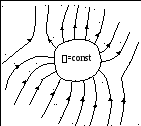 ,
,
quelli. intensità di campo all'interno del conduttore:
Pertanto, dall'uguaglianza otteniamo ![]() all'interno del conduttore. Pertanto, questa condizione è soddisfatta anche al confine del conduttore. Quelli. la superficie del conduttore è equipotenziale
superficie
, Ecco perchè linee di forza campo elettrico perpendicolare alla superficie del conduttore in ogni punto
.
all'interno del conduttore. Pertanto, questa condizione è soddisfatta anche al confine del conduttore. Quelli. la superficie del conduttore è equipotenziale
superficie
, Ecco perchè linee di forza campo elettrico perpendicolare alla superficie del conduttore in ogni punto
.
conduttore carico .
Se una carica elettrica esterna viene impartita a un conduttore solitario, la condizione di equilibrio di carica porta nuovamente alla condizione:
,![]() all'interno del conduttore.
all'interno del conduttore.
Ne consegue che tutte le cariche esterne si trovano sulla superficie del conduttore, perché. l'intensità di campo all'interno del conduttore è zero e secondo il teorema di Gauss per qualsiasi superficie chiusa all'interno del conduttore (compresa la superficie esterna del conduttore):
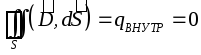 .
.
Poiché anche la superficie del conduttore in questo caso è equipotenziale, le linee di forza del campo elettrico sono dirette perpendicolarmente alla superficie del conduttore in ciascuno dei suoi punti.
Dal teorema di Gauss segue quello vicino alla superficie del conduttore
L'entità del vettore di spostamento elettrico è uguale alla densità superficiale delle cariche esterne.
La carica sulla superficie del conduttore è distribuita in modo tale che il potenziale superficiale rimanga costante. Ciò porta al fatto che la densità di carica sulla superficie del conduttore non è la stessa. Ad esempio, sulle parti taglienti dei conduttori, la densità di carica è maggiore che nei recessi. A questo proposito, sorgono vari fenomeni, ad esempio "charge drain". Se il conduttore è nell'aria, la ionizzazione dell'aria avviene vicino alla punta, portando via parte della carica elettrica, un fenomeno chiamato "vento elettrico".
Metodo di imaging elettrico .
Se la superficie equipotenziale viene sostituita da una superficie conduttrice e quindi la parte del campo che questa superficie separa viene scartata, il modello di campo nella parte rimanente non cambierà. Al contrario, se l'immagine del campo è integrata con cariche fittizie in modo che la superficie conduttrice possa essere sostituita da una equipotenziale, l'immagine del campo iniziale non cambierà.
Esempio.Trova la forza di attrazione di una carica puntiforme su un piano conduttore infinito
. Per fare ciò, integreremo l'immagine con un'altra carica dello stesso tipo, ma di segno opposto, situata simmetricamente rispetto al piano. Quindi il piano coinciderà con la superficie equipotenziale, quindi il piano può essere scartato e si può trovare la forza di interazione tra le cariche: 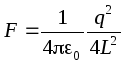 .
.
L'energia di un conduttore carico .
L'energia di un conduttore carico solitario è definita come l'energia di un sistema di cariche: 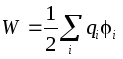 . Sul conduttore, quindi l'energia di un conduttore solitario:
. Sul conduttore, quindi l'energia di un conduttore solitario:
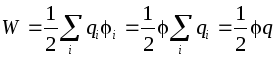 .
.
Per un sistema di conduttori carichi: 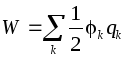 .
.
In particolare, per due conduttori aventi cariche q di uguale grandezza ma di segno diverso, l'energia sarà pari a: 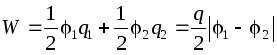 .
.
Commento
. L'entità della differenza di potenziale ![]() chiamato voltaggio
tra corpi.
chiamato voltaggio
tra corpi.
L'esperienza mostra che esiste una relazione lineare tra la carica di un conduttore solitario e il suo potenziale: . Fattore di proporzionalità DA chiamato coefficiente di elettrico
contenitori o capacità elettrica
.
L'unità di capacità elettrica è Farad ( 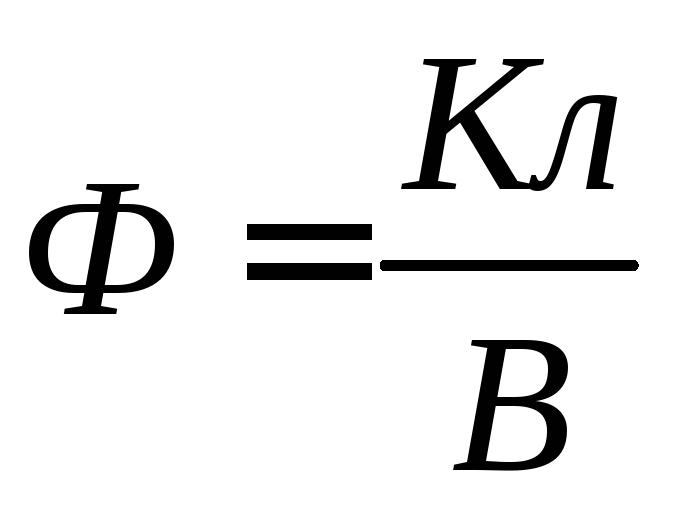 ).
).
Condensatore è chiamato un sistema di due conduttori carichi della stessa magnitudine, ma diversi nelle cariche di segno. Si chiamano i conduttori piastre di condensatori .
La capacità di un condensatore è determinata dalla formula.
Il condensatore è convenzionalmente designato.
Collegamento di condensatori
Considera una connessione in serie di due condensatori C 1 e C 2. Il punto A tra i condensatori è separato dal resto del circuito, quindi la sua carica elettrica non può cambiare. Poiché la carica iniziale di qualsiasi punto era uguale a zero, quindi ![]() . Di conseguenza, le cariche delle piastre del condensatore adiacenti al punto A sono uguali in grandezza, ma di segno opposto. Ma poiché il valore della carica delle piastre è uguale alla carica dei condensatori, allora. La carica totale del punto A è zero, quindi se scartiamo questo punto insieme alle piastre, non cambierà nulla nel circuito. Perché anche le cariche delle piastre estreme sono le stesse in grandezza, ma di segno diverso, quindi il condensatore risultante avrà la stessa carica in grandezza.
. Di conseguenza, le cariche delle piastre del condensatore adiacenti al punto A sono uguali in grandezza, ma di segno opposto. Ma poiché il valore della carica delle piastre è uguale alla carica dei condensatori, allora. La carica totale del punto A è zero, quindi se scartiamo questo punto insieme alle piastre, non cambierà nulla nel circuito. Perché anche le cariche delle piastre estreme sono le stesse in grandezza, ma di segno diverso, quindi il condensatore risultante avrà la stessa carica in grandezza.
TOTALE . Le cariche dei condensatori collegati in serie hanno la stessa intensità. La carica totale dei condensatori collegati in serie è uguale alla carica di ciascuno dei condensatori.
In questo caso, la tensione totale è uguale alla somma delle tensioni sui condensatori: U GENERALE \u003d U 1 + U 2. Le cariche dei condensatori sono le stesse: q 1 \u003d q 2 \u003d q. Quindi 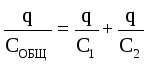 . Ecco perchè
. Ecco perchè 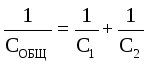 .
.
Quando i condensatori sono collegati in serie, le loro capacità vengono sommate secondo la legge dei reciproci .
Calcolo della capacità per il collegamento in parallelo di condensatori.
In questo caso, le tensioni sui condensatori sono le stesse: U 1 \u003d U 2 \u003d U.
La carica totale è uguale alla somma delle cariche: q GEN = q 1 + q 2 o C GEN U=C 1 U+C 2 U.
Allora C GENERALE =C 1 +C 2 . Quando i condensatori sono collegati in parallelo, le loro capacità si sommano.
Energia del condensatore :
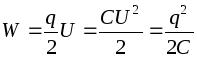 .
.
La carica totale del condensatore è zero. Un condensatore immagazzina energia elettrica separando le cariche elettriche.
Esempi per calcolare la capacità dei condensatori .
Condensatore piatto (ad aria). rappresenta due lastre parallele, la cui distanza è molto inferiore alle dimensioni delle lastre, per cui il campo tra le lastre può considerarsi uniforme. C'è un vuoto (aria) tra le piastre, quindi = 1.
 In questo caso, quando si calcola il pattern di campo, è possibile utilizzare i risultati ottenuti per il campo di un piano a carica infinita. Poiché le cariche e le aree delle piastre sono uguali in grandezza, l'intensità dell'intensità di campo creata da ciascuna delle piastre è la stessa: ma le direzioni dei vettori di intensità sono diverse (viene mostrato il vettore di intensità di una piastra caricata negativamente da una linea tratteggiata). Tra le piastre, i vettori di intensità sono diretti allo stesso modo, quindi l'intensità totale è uguale alla somma delle intensità di campo create da ciascuna delle piastre:
In questo caso, quando si calcola il pattern di campo, è possibile utilizzare i risultati ottenuti per il campo di un piano a carica infinita. Poiché le cariche e le aree delle piastre sono uguali in grandezza, l'intensità dell'intensità di campo creata da ciascuna delle piastre è la stessa: ma le direzioni dei vettori di intensità sono diverse (viene mostrato il vettore di intensità di una piastra caricata negativamente da una linea tratteggiata). Tra le piastre, i vettori di intensità sono diretti allo stesso modo, quindi l'intensità totale è uguale alla somma delle intensità di campo create da ciascuna delle piastre:
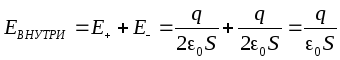 .
.
All'esterno delle piastre, i vettori di intensità di campo sono diretti in modo opposto, quindi l'intensità di campo all'esterno è zero. In questo modo, in un condensatore, l'intensità del campo è diversa da zero solo tra le piastre.
Poiché il campo elettrostatico è un campo di forza conservativa, l'integrale 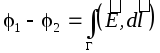 non dipende dalla forma della traiettoria G, quindi la differenza di potenziale tra le piastre può essere trovata lungo la perpendicolare che collega le piastre, la cui lunghezza è pari a d:
non dipende dalla forma della traiettoria G, quindi la differenza di potenziale tra le piastre può essere trovata lungo la perpendicolare che collega le piastre, la cui lunghezza è pari a d: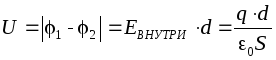 , dove dè la distanza tra i piatti. Quindi la capacità di un condensatore piatto (ad aria) secondo la definizione sarà uguale a:
, dove dè la distanza tra i piatti. Quindi la capacità di un condensatore piatto (ad aria) secondo la definizione sarà uguale a: 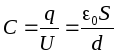
Condensatore cilindrico (ad aria). è costituito da due cilindri coassiali
della stessa lunghezza, annidati l'uno nell'altro in modo che la distanza tra le piastre sia molto inferiore alle dimensioni delle piastre.
Sia la lunghezza del condensatore l, la carica del rivestimento interno è positiva: q > 0. Raggi di placcatura R 1 e R 2, lascia R 1 <R 2. Intensità di campo tra le piastre a distanza r dal rivestimento interno, cioè per R 1 <r <R 2 , troviamo usando il teorema di Gauss:
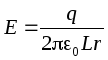 .
.
Quindi la tensione tra le piastre: .
Pertanto, la capacità elettrica di un condensatore cilindrico (ad aria): ![]() .
.
DA  condensatore sferico (ad aria).
rappresenta due sfere concentriche annidate con i raggi delle piastre R 1 e R 2 ,R 1 <R 2. Sia la carica del rivestimento interno q> 0. L'intensità del campo tra i rivestimenti a distanza r dal rivestimento interno ( R 1
<r
<R 2) troviamo per il teorema di Gauss:
condensatore sferico (ad aria).
rappresenta due sfere concentriche annidate con i raggi delle piastre R 1 e R 2 ,R 1 <R 2. Sia la carica del rivestimento interno q> 0. L'intensità del campo tra i rivestimenti a distanza r dal rivestimento interno ( R 1
<r
<R 2) troviamo per il teorema di Gauss:
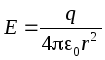 .
.
Tensione tra le piastre: .
Pertanto, la capacità di un condensatore sferico (ad aria). ![]() .
.
Densità di energia volumetrica del campo elettrostatico.
Considera un condensatore ad aria piatto. Energia di un condensatore carico
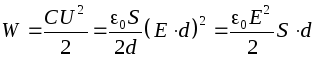 .
.
La quantità di spazio tra le piastre di un condensatore. Poiché il campo tra le piastre è considerato omogeneo, il volume unitario di questo campo ha l'energia 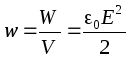 . Questo valore viene chiamato densità di energia volumetrica
.
. Questo valore viene chiamato densità di energia volumetrica
.
Nel caso in cui il campo non sia uniforme, la densità di energia volumetrica è .
Nella materia, la densità di energia volumetrica del campo elettrico 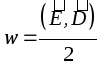 .
.
Nel caso di un dielettrico isotropo omogeneo, quindi 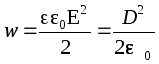 .
.
Perché ![]() , poi
, poi 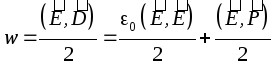 , dove
, dove
L'energia del campo elettrico nel vuoto è l'energia della polarizzazione della materia.
Esempio . Si consideri una sfera carica con pareti sottili di raggio R. Poiché le cariche con lo stesso nome si respingono sulla sfera, le forze repulsive tendono ad allungare la superficie della sfera. Possiamo supporre che dall'interno della sfera, le pareti siano interessate pressione aggiuntiva p, facendo scoppiare la sfera e causato dalla presenza di una carica elettrica sulla superficie. Cerchiamo R.
L'intensità del campo all'interno della sfera è zero, quindi la densità di energia del volume del campo elettrico wè diverso da zero solo al di fuori della sfera.
Con un leggero aumento del raggio della sfera di dR il suo volume aumenterà, mentre in quella parte dello spazio circostante che è entrata all'interno della sfera, la densità di energia volumetrica diventerà pari a zero. Pertanto, la variazione dell'energia del campo esterno sarà uguale a, dove Sè la superficie. Ma con l'espansione della sfera, le forze di pressione all'interno della sfera faranno il lavoro ![]() . Da allora
. Da allora ![]() da dove.
da dove.
Esempio . Troviamo le forze che agiscono sulle piastre in un condensatore piatto carico, scollegato dalla fonte di alimentazione.
Le piastre sono caricate in modo opposto, quindi si attraggono. Supponiamo che i piatti siano vicini l'uno all'altro di una piccola quantità. X. Quindi il volume del condensatore viene ridotto di dV = xS, quindi l'energia del condensatore è diminuita di dW = wdV. Le forze attrattive funzionano UN = fx. Poiché A= dW, poi fx = wxS. Pertanto, l'entità della forza è F = wS. La pressione aggiuntiva che queste forze creano è uguale a.
Gli esempi precedenti mostrano che i corpi in un campo elettrico sono soggetti a forze che causano una pressione aggiuntiva pari alla densità di energia volumetrica.
La pressione causata dalla presenza di un campo elettrico è uguale alla densità di energia volumetrica .
Forze , agendo sul corpo dal lato di qualche campo, sono chiamati podemotor .
Le piastre del condensatore con carica opposta si attraggono.
Si chiamano forze meccaniche agenti su corpi carichi macroscopiciponderomotivo .
Calcoliamo le forze ponderomotrici agenti sulle piastre di un condensatore piatto. In questo caso sono possibili due opzioni:
Il condensatore viene caricato e scollegato dalla batteria carica(in questo caso il numero di cariche sulle piastre rimane costante q = cost).
Quando una piastra di un condensatore viene rimossa dall'altra, il lavoro è terminato
per cui l'energia potenziale del sistema aumenta:
In questo caso, dA = dW . Uguagliando i lati destri di queste espressioni, otteniamo
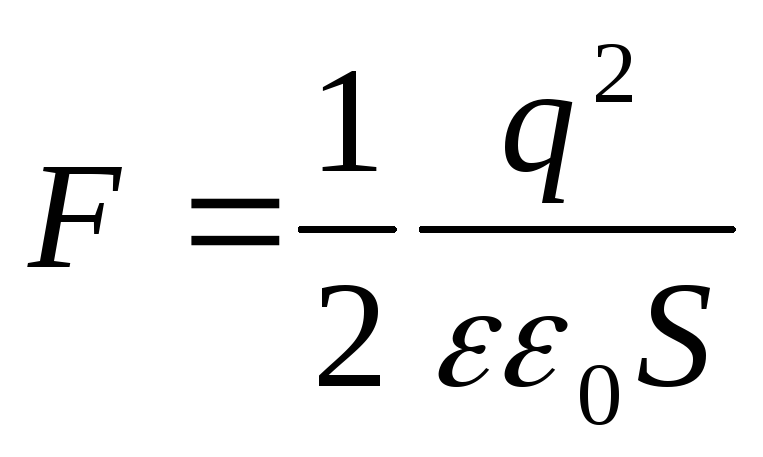 (12.67)
(12.67)
In questo caso, durante la differenziazione, la distanza tra le piastre è stata designata x.
Condensatore carico ma non scollegato dalla batteria(in questo caso, spostando una delle piastre del condensatore, la tensione rimarrà costante ( u = cost). In questo caso, quando una piastra si allontana dall'altra, l'energia potenziale del campo del condensatore diminuisce, poiché le cariche "perdono" dalle piastre, quindi
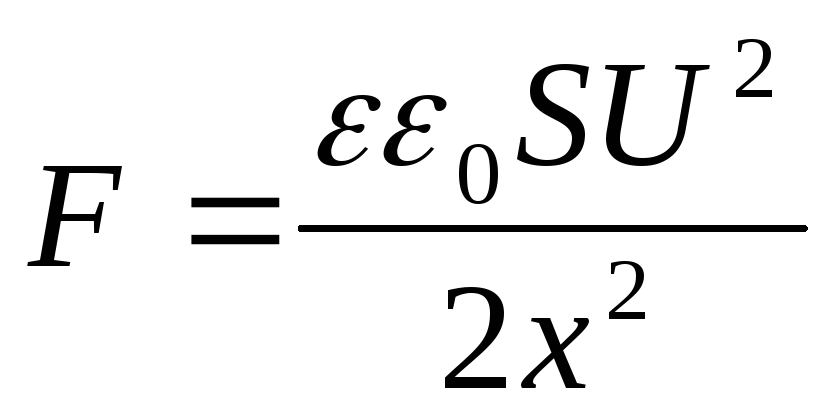
Ma 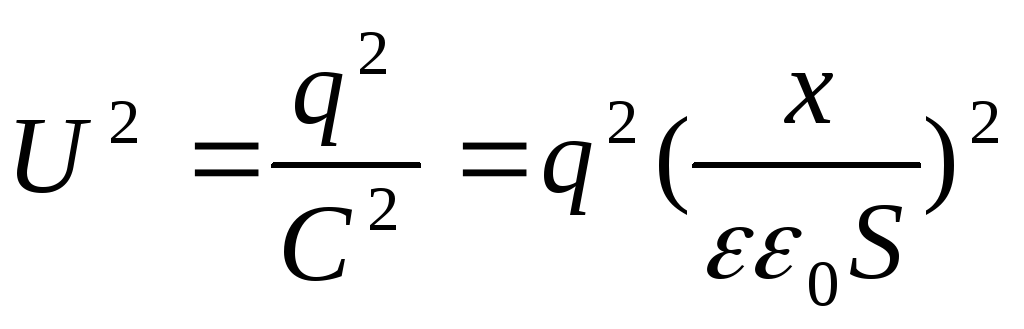 , poi
, poi
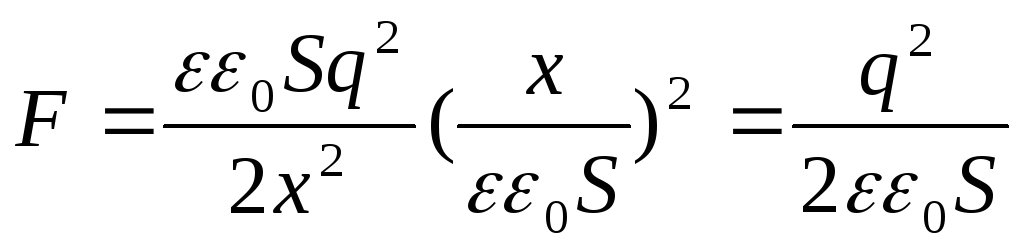
L'espressione risultante coincide con la formula 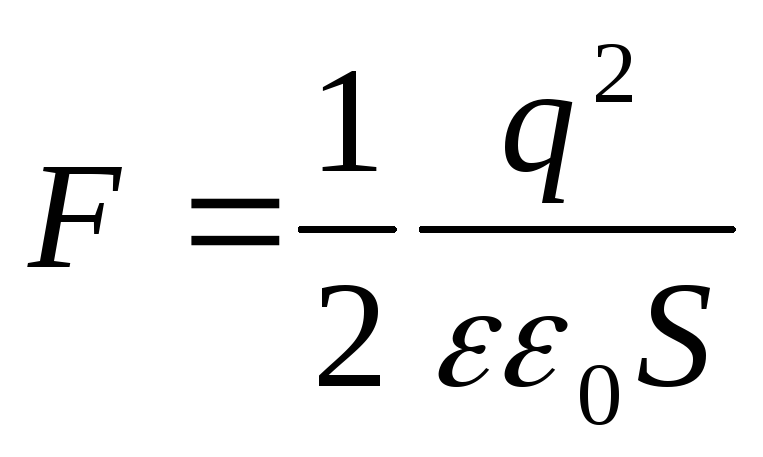 . Può anche essere rappresentato in un'altra forma se al posto della carica q introduciamo la densità superficiale:
. Può anche essere rappresentato in un'altra forma se al posto della carica q introduciamo la densità superficiale:
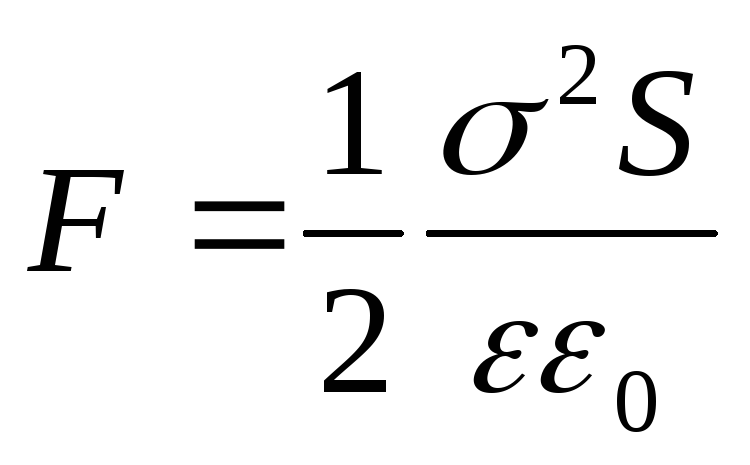 (12.68)
(12.68)
Il campo è uniforme. L'intensità di campo del condensatore è 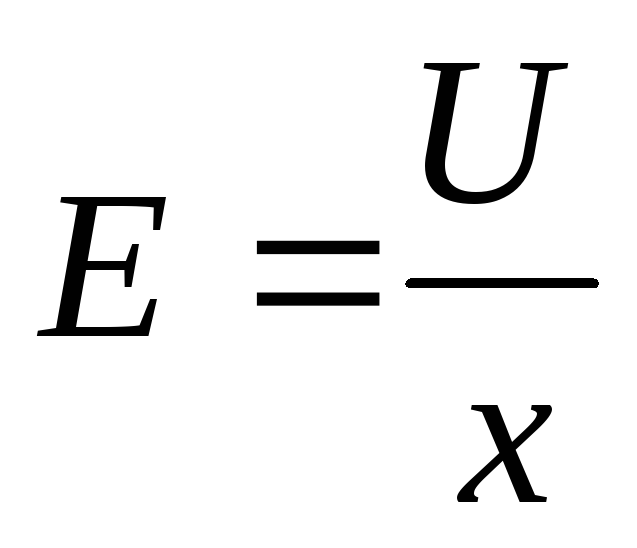 , dove x è la distanza tra le piastre. Sostituendo nella formula
, dove x è la distanza tra le piastre. Sostituendo nella formula 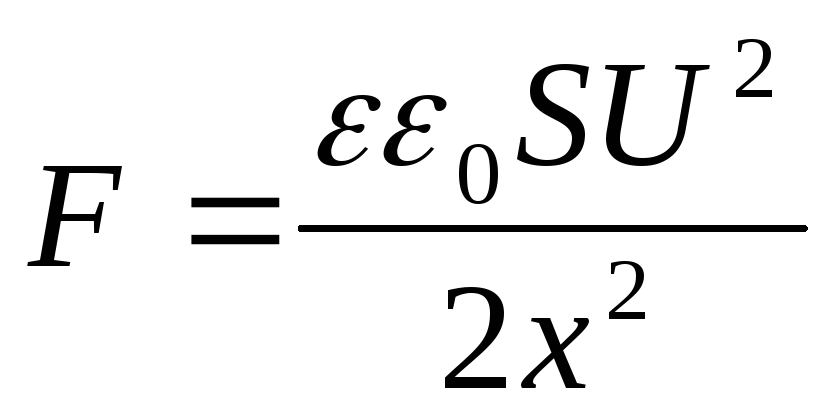 U 2 \u003d E 2 x 2, otteniamo che la forza di attrazione delle piastre di un condensatore piatto
U 2 \u003d E 2 x 2, otteniamo che la forza di attrazione delle piastre di un condensatore piatto
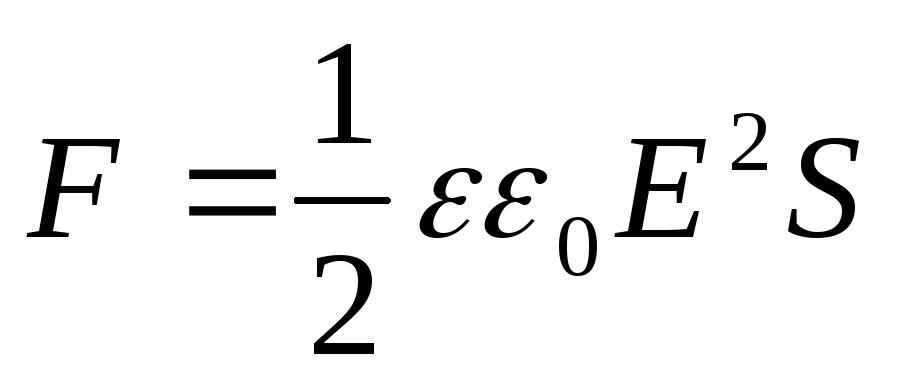 (12.69)
(12.69)
Queste forze agiscono non solo sulle piastre. Poiché le piastre, a loro volta, esercitano pressione sul dielettrico interposto tra loro e lo deformano, si crea pressione nel dielettrico
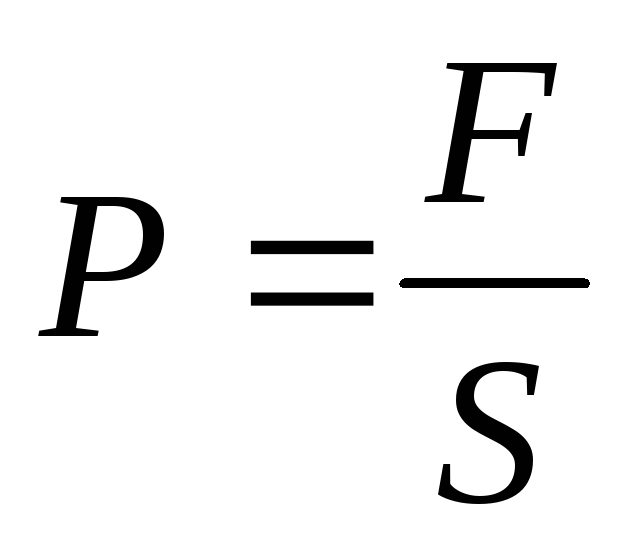
(S è l'area di ogni piatto).
La pressione che si forma nel dielettrico è
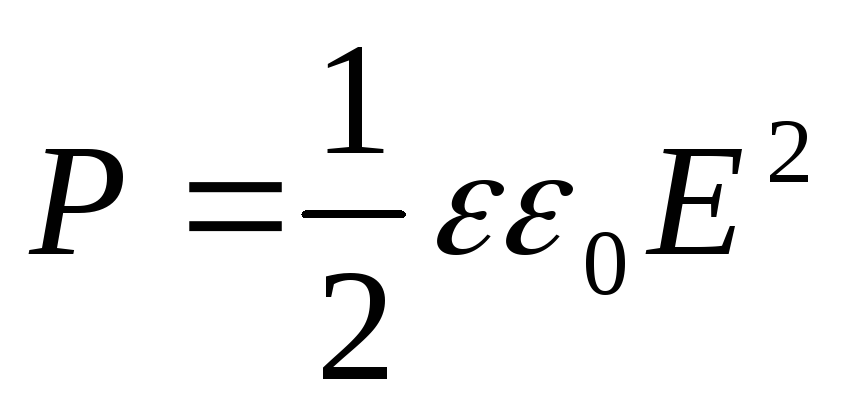 (12.70)
(12.70)
Esempi di problem solving
Esempio 12.5. Una differenza di potenziale di 1,5 kV viene applicata alle piastre di un condensatore ad aria piatta. Superficie del piatto 150 cm 2 e la distanza tra loro è di 5 mm. Dopo aver scollegato il condensatore dalla sorgente di tensione, il vetro è stato inserito nello spazio tra le piastre (ε 2 =7) Definire:
1) differenza di potenziale tra le piastre dopo l'introduzione di un dielettrico; 2) la capacità del condensatore prima e dopo l'introduzione del dielettrico; 3) la densità di carica superficiale sulle piastre prima e dopo l'introduzione del dielettrico.
Dato: U 1 \u003d 1,5 kV \u003d 1,5 ∙ 10 3 V; S \u003d 150 cm 2 \u003d 1,5 ∙ 10 -2 m 2; ε 1 = 1; d=5mm=5∙10 -3 m.
Trova: 1) U2; 2) C 1 C 2; 3) σ 1 , σ 2
Soluzione
.
Perché 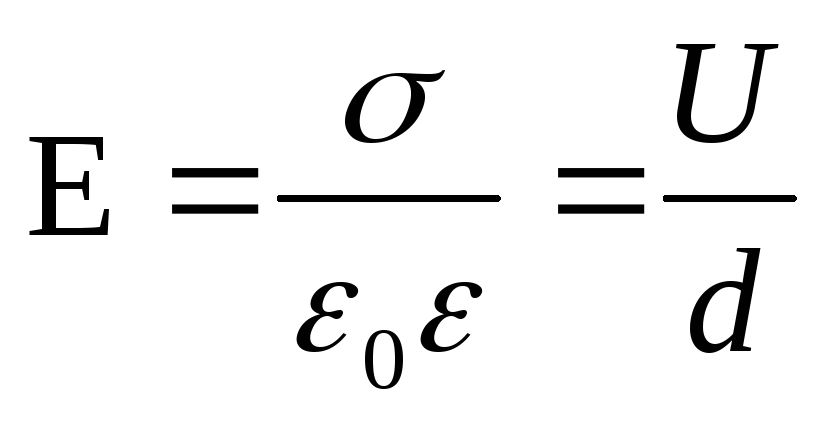 (σ è la densità di carica superficiale sulle piastre del condensatore), quindi prima dell'introduzione del dielettrico σd \u003d U 1 ε 0 ε 1 e dopo l'introduzione del dielettrico σd \u003d U 2 ε 0 ε 2, quindi
(σ è la densità di carica superficiale sulle piastre del condensatore), quindi prima dell'introduzione del dielettrico σd \u003d U 1 ε 0 ε 1 e dopo l'introduzione del dielettrico σd \u003d U 2 ε 0 ε 2, quindi
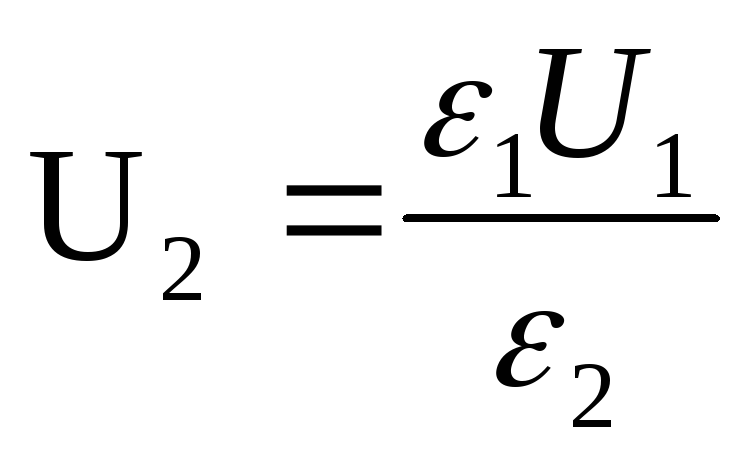
La capacità del condensatore prima e dopo l'introduzione di un dielettrico
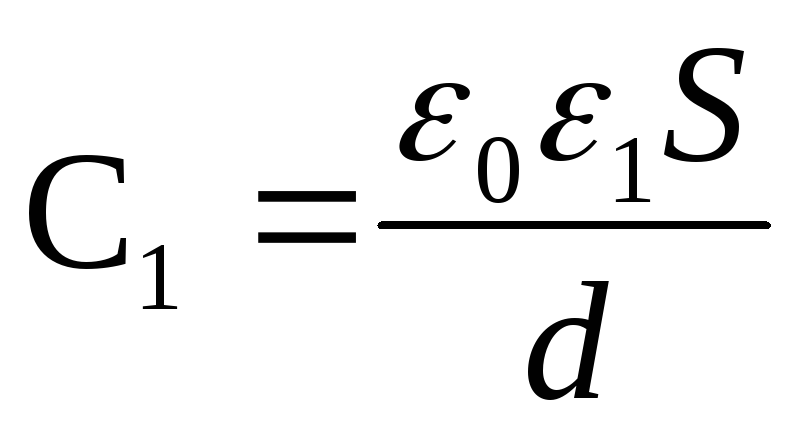 e
e 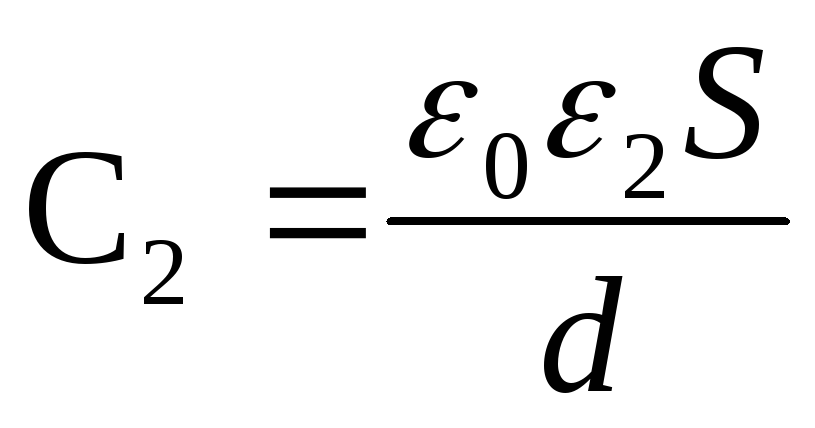
La carica delle piastre dopo la disconnessione dalla fonte di tensione non cambia, ad es. q=cost. Pertanto, la densità di carica superficiale sulle piastre prima e dopo l'introduzione del dielettrico
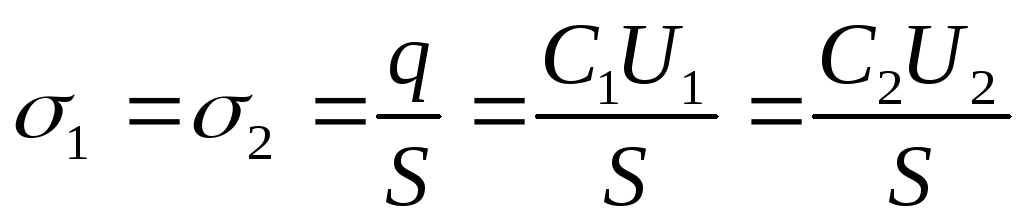
Risposta: 1) U 2 \u003d 214V; 2) C 1 \u003d 26,5 pF; C 2 \u003d 186pF; 3) σ 1 = σ 2 = 2,65 μC/m 2.
Esempio 12.7. Lo spazio tra le piastre di un condensatore piatto è riempito con un dielettrico anisotropo, la cui permeabilità ε varia nella direzione perpendicolare alle piastre secondo la legge lineareε = α + βх da ε 1 fino a ε 2 , e ε 2 > ε 1 . L'area di ogni rivestimentoS, la distanza tra lorod. Trova la capacità del condensatore.
Dato:S; d; ε 1 ; ε 2
Trova: DA.
Soluzione
.
La costante dielettrica ε
varia linearmente, ε = α + βx, dove x è misurata dal rivestimento, la cui permeabilità è pari a ε 1 . Considerando che ε (0) = ε 1 , ε (d) = ε 2 , otteniamo la dipendenza 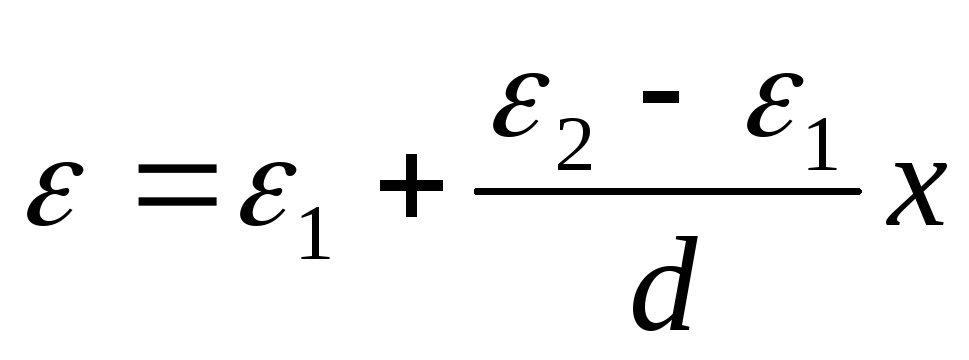 . Trova la differenza di potenziale tra le piastre:
. Trova la differenza di potenziale tra le piastre:
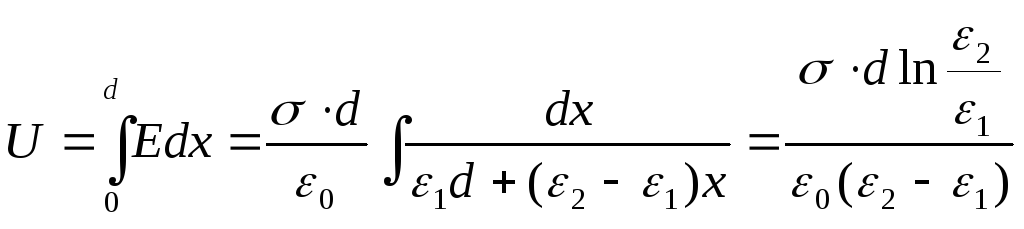
La capacità del condensatore sarà
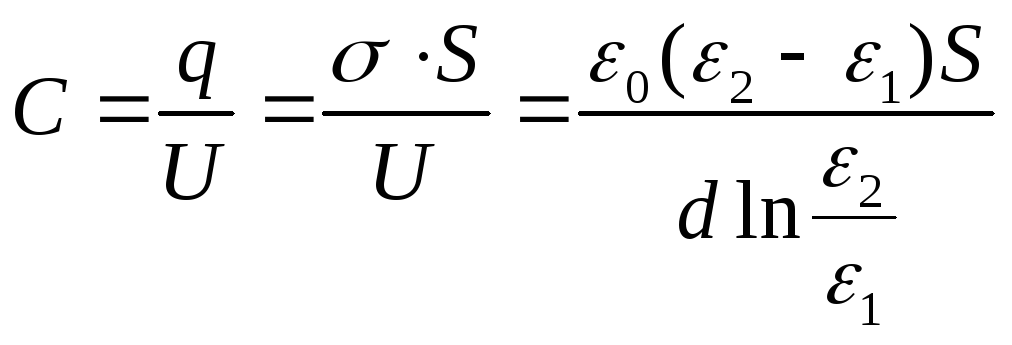
Risposta:
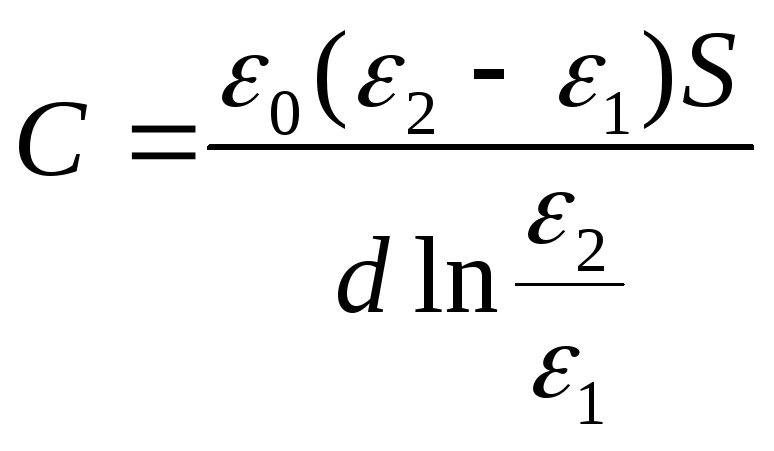
Esempio 12.7. Tra le piastre di un condensatore piatto carico di una differenza di potenziale u , due strati di dielettrico sono posti parallelamente alle sue piastre. Lo spessore degli strati e la permittività dei dielettrici sono rispettivamented 1 , d 2 , ε 1 , ε 2 . Determinare l'intensità dei campi elettrostatici negli strati dielettrici.
Dato: u; d 1 , d 2 , ε 1 , ε 2
Trova: E1, E2.
Soluzione . La tensione attraverso le piastre del condensatore, dato che il campo all'interno di ciascuno degli strati dielettrici è uniforme,
U=MI 1 g 1 + MI 2 g 2 . (uno)
Lo spostamento elettrico in entrambi gli strati dielettrici è lo stesso, quindi possiamo scrivere
D=D1=D2= ε 0 ε 1 E1 = ε 0 ε 2 E 2 (2)
Dalle espressioni (1) e (2) troviamo il desiderato
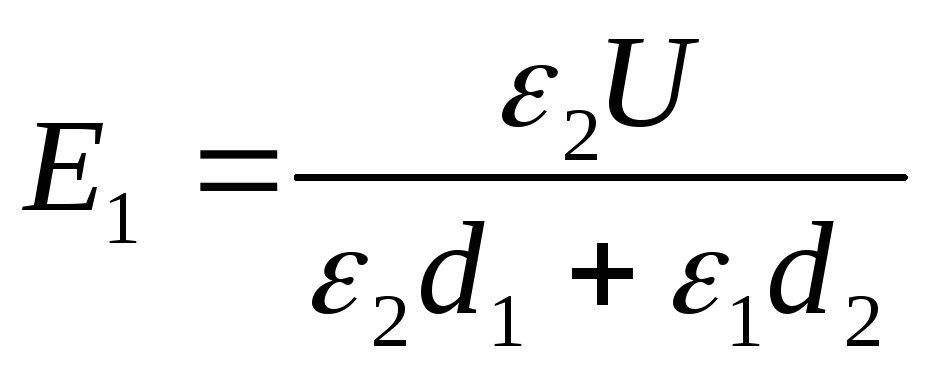 (3)
(3)
Dalla formula (2) segue che
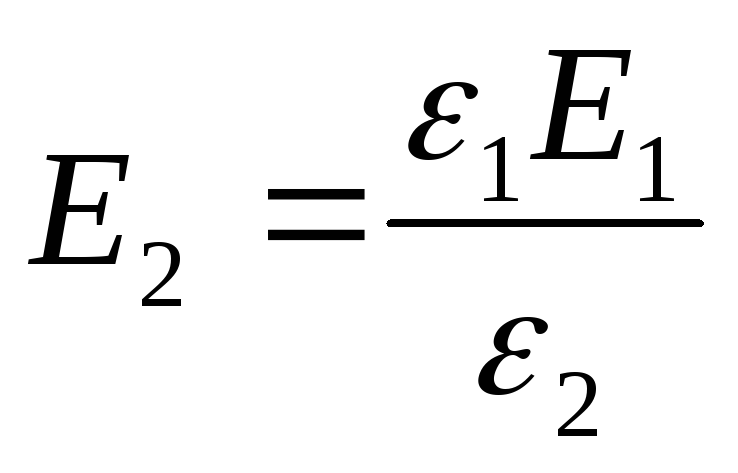
Risposta:
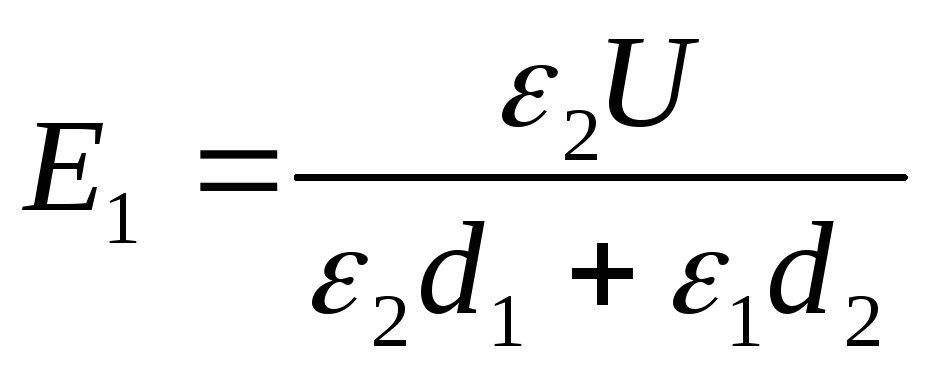 ;
;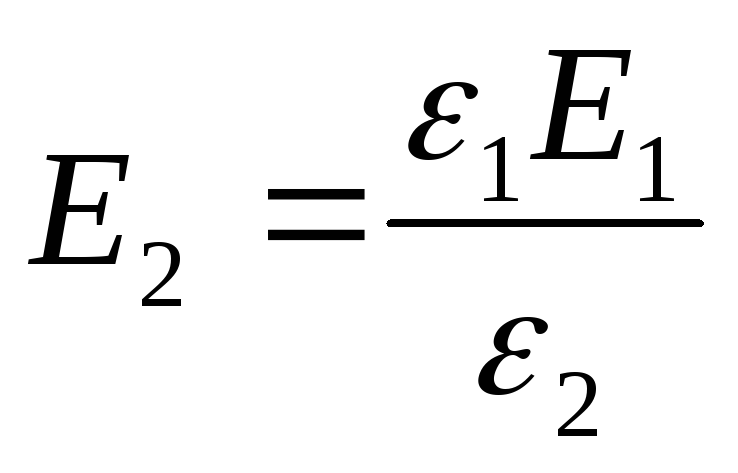
Esempio 12.7. Zona del piatto S il condensatore piatto è di 100 cm 2 . Lo spazio tra le piastre è riempito strettamente con due strati di dielettrico: una piastra di mica (ε 1 =7) spesso d 1 =3,5 mm e paraffina (ε 2 =2) spessore d 2 = 5 mm. Determina la capacità di questo condensatore.
Dato: S= 100 cm 2 =10 -2 m 2 ; ε 1 =7; d 1 =3,5 mm=3,5∙10 -3 m;, ε 1 =2; d 1 =3,5mm=5∙10 -3 m;
Trova: DA.
Soluzione . Capacità del condensatore
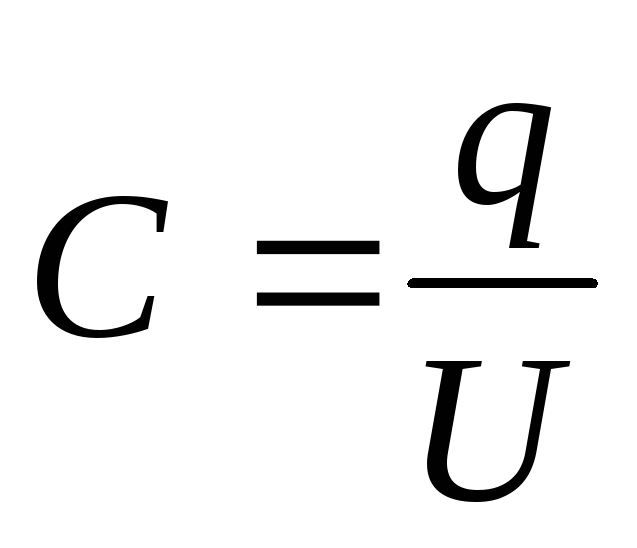
dove = - carica sulle piastre del condensatore (- densità di carica superficiale sulle piastre); \u003d - differenza di potenziale delle piastre, uguale alla somma delle tensioni sugli strati dielettrici: U \u003d U 1 +U 2. Quindi
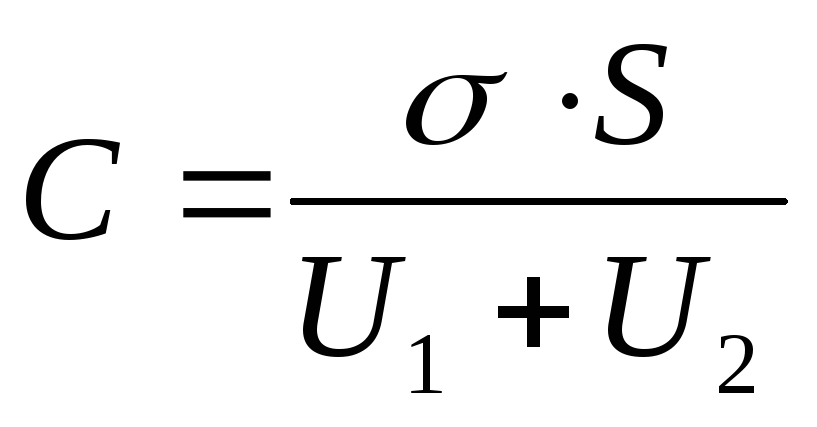 (1)
(1)
Le tensioni U 1 e U 2 si trovano dalle formule
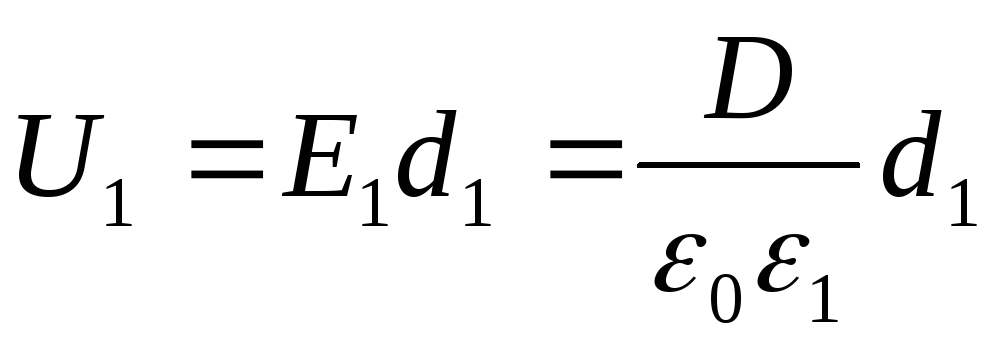 ;
;
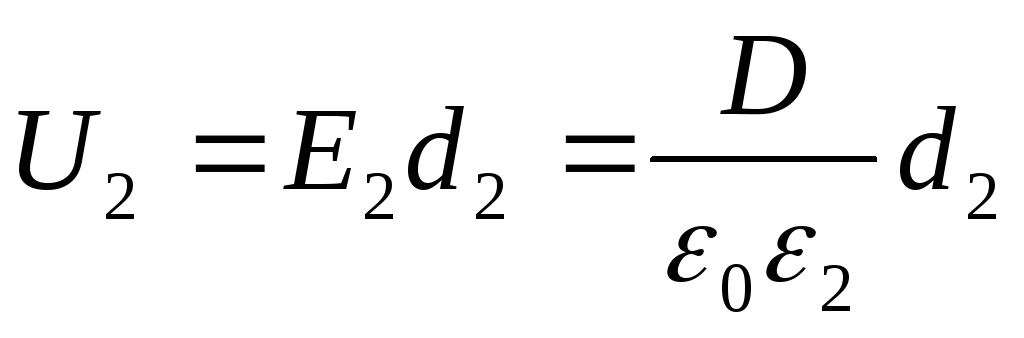 (2)
(2)
dove E 1 ed E 2 - l'intensità del campo elettrostatico nel primo e nel secondo strato del dielettrico; D è lo spostamento elettrico nei dielettrici (lo stesso in entrambi i casi). Tenendo conto che
E data la formula (2), dall'espressione (1) troviamo la capacità desiderata del condensatore
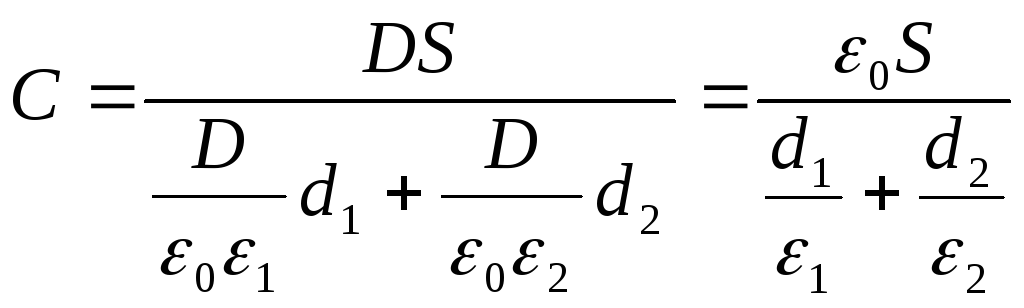
Risposta: C \u003d 29,5 pF.
Esempio 12.7. Una batteria di tre condensatori collegati in serie C 1 \u003d 1 μF; DA 2 \u003d 2uF e C 3 \u003d 4 μF sono collegati a una sorgente EMF. Carica della batteria del condensatore q \u003d 40 μC. Determina: 1) tensione u 1 , u 2 e u 3 su ciascun condensatore; 2) sorgente EMF; 3) la capacità del banco di condensatori.
Dato : C 1 \u003d 1 μF \u003d 1 ∙ 10 -6 F; C 2 \u003d 2 μF \u003d 2 ∙ 10 -6 F e C 3 \u003d 4 μF \u003d 4 ∙ 10 -6 F; q \u003d 40 μC \u003d 40 ∙ 10 -6 F .
Trova: 1) U1, U2, U3 ; 2) ξ; 3) C.
Soluzione . Quando i condensatori sono collegati in serie, le cariche di tutte le piastre sono quindi uguali in valore assoluto
q 1 \u003d q 2 \u003d q 3 \u003d q.
Tensione del condensatore
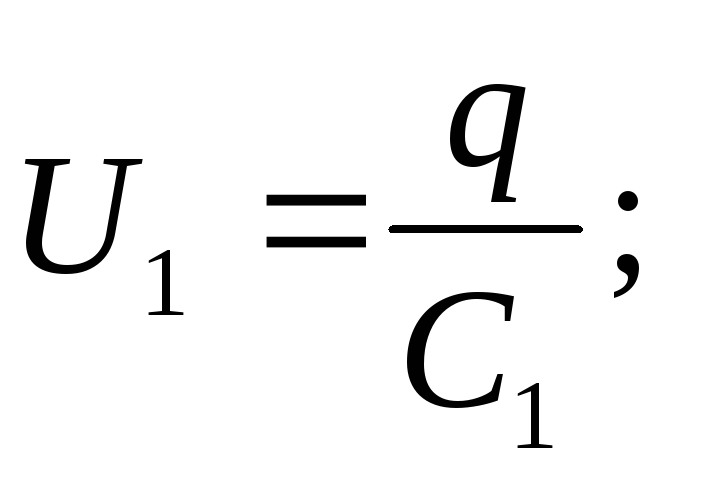
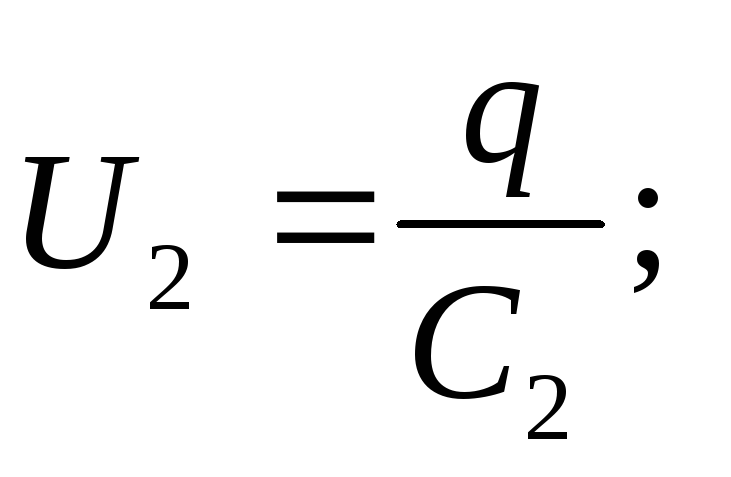
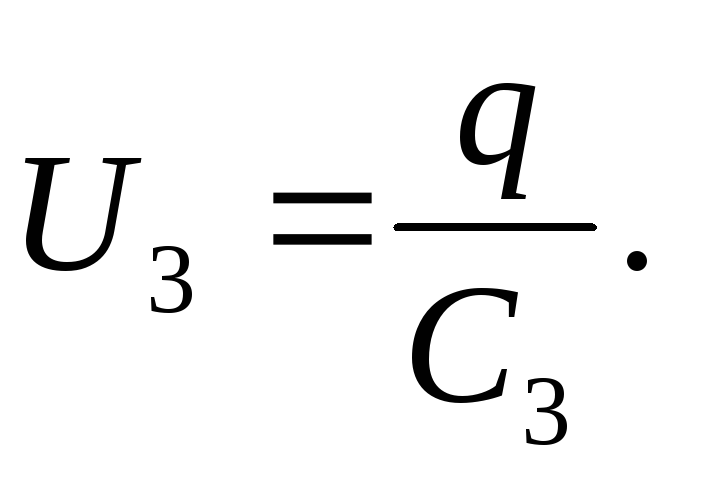
L'EMF della sorgente è uguale alla somma delle tensioni di ciascuno dei condensatori collegati in serie:
ξ \u003d U 1 + U 2 + U 3
Quando sono collegati in serie, si sommano i reciproci delle capacità di ciascuno dei condensatori:
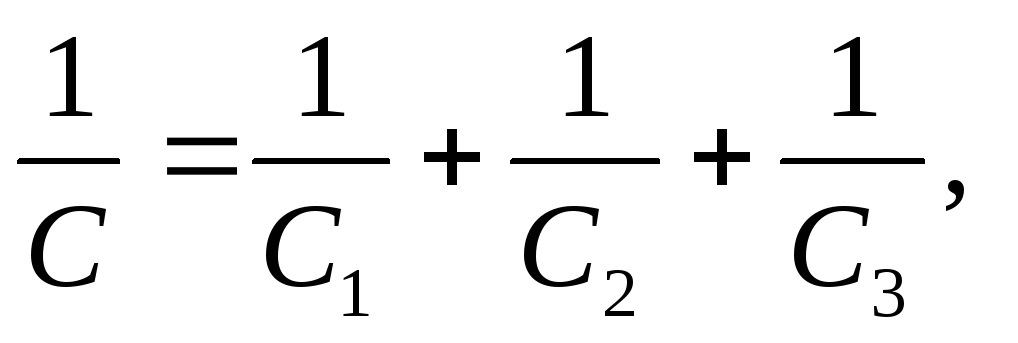
Dov'è la capacità desiderata del banco di condensatori
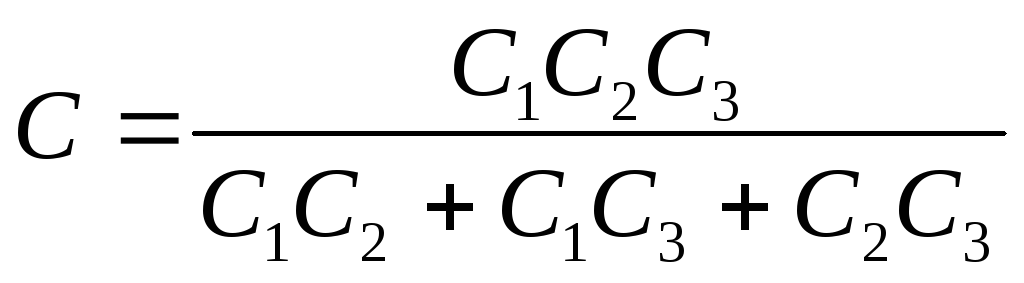
Risposta 1) U 1 \u003d 40 V; U 2 \u003d 20 V, U 3 = 10V; 2) Ɛ= 70V; 3) C \u003d 0,571 μF.
Esempio 12.7. Due condensatori ad aria piatta della stessa capacità sono collegati in serie e collegati a una sorgente EMF. Come e quante volte cambierà la carica dei condensatori se uno di essi è immerso in olio con costante dielettrica ε=2,2.
Dato: C 1 \u003d C 2 \u003d C; q \u003d 40 μC \u003d 40 ∙ 10 -6 F ; ε 1 =1; ε 2 =2,2.
Trova:
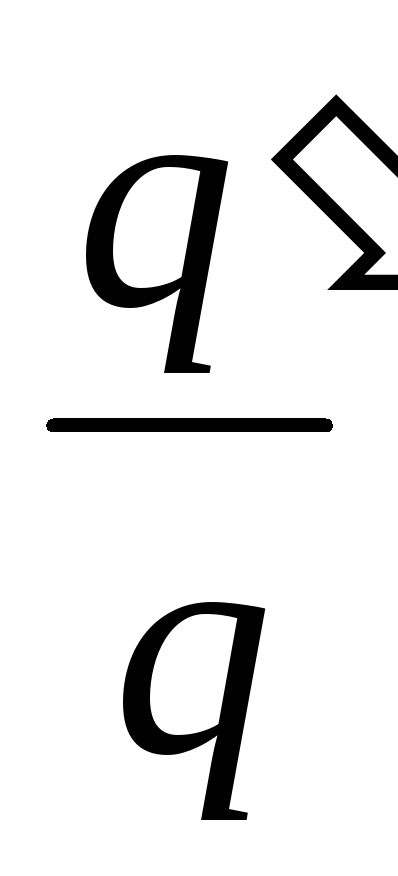 .
.
Soluzione . Quando i condensatori sono collegati in serie, le cariche di entrambi i condensatori sono uguali in grandezza. Prima dell'immersione in un dielettrico (in olio), la carica di ogni condensatore
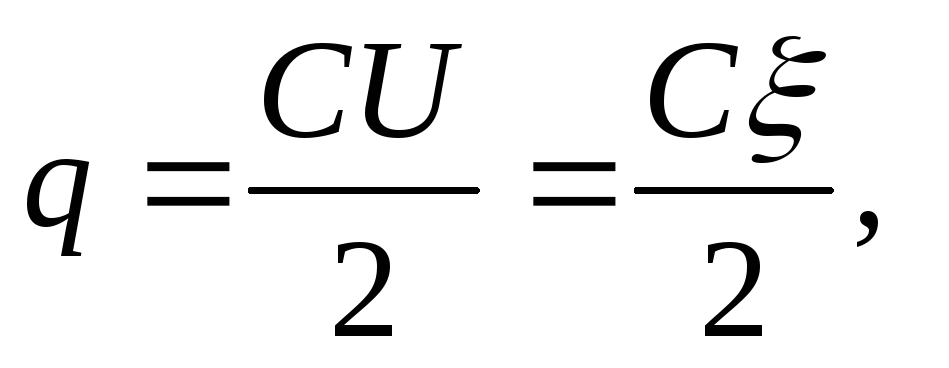
dove ξ \u003d U 1 + U 2 (quando i condensatori sono collegati in serie, l'EMF della sorgente è uguale alla somma delle tensioni di ciascuno dei condensatori).
Dopo che uno dei condensatori è stato immerso in un dielettrico, le cariche dei condensatori sono di nuovo le stesse e, rispettivamente, sul primo e sul secondo condensatore sono uguali
q= CU 1 =ε 2 CU 2
(tenendo conto che ε 1 =1), per cui, se teniamo conto che ξ = U 1 + U 2 , troviamo
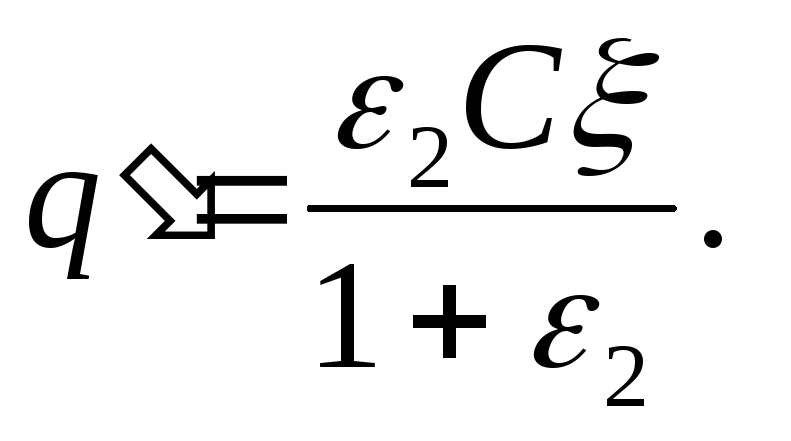 (2)
(2)
Dividendo (2) per (1), troviamo il rapporto desiderato
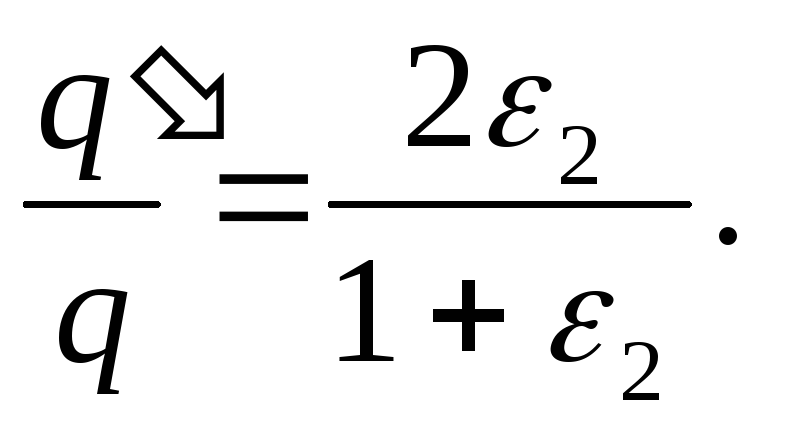
Risposta:
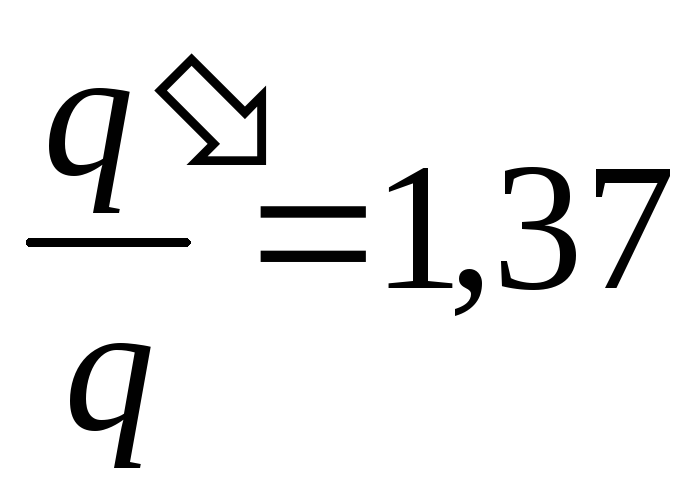 , cioè. la carica dei condensatori aumenta di un fattore 1,37.
, cioè. la carica dei condensatori aumenta di un fattore 1,37.
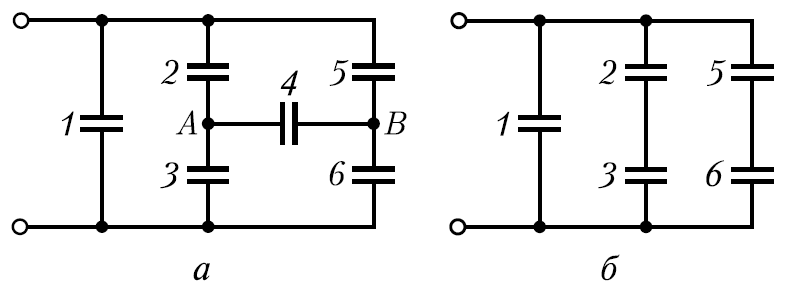
Esempio 12.7. I condensatori con capacità C ciascuno sono collegati come mostrato in fig.a. determinare la capacità Comune questo collegamento di condensatori. .
 Soluzione
.
Se si scollega il condensatore C 4 dal circuito, si ottiene una connessione di condensatori, che è facilmente calcolabile. Poiché le capacità di tutti i condensatori sono le stesse (C 2 \u003d C 3 e C 5 \u003d C 6), entrambi i rami paralleli sono simmetrici, quindi i potenziali dei punti A e B, ugualmente situati nei rami, devono essere uguali. Il condensatore C 4 è quindi collegato a punti con differenza di potenziale nulla. Pertanto, il condensatore C 4 non è carico, ad es. può essere escluso e lo schema presentato nella condizione del problema può essere semplificato (Fig. b).
Soluzione
.
Se si scollega il condensatore C 4 dal circuito, si ottiene una connessione di condensatori, che è facilmente calcolabile. Poiché le capacità di tutti i condensatori sono le stesse (C 2 \u003d C 3 e C 5 \u003d C 6), entrambi i rami paralleli sono simmetrici, quindi i potenziali dei punti A e B, ugualmente situati nei rami, devono essere uguali. Il condensatore C 4 è quindi collegato a punti con differenza di potenziale nulla. Pertanto, il condensatore C 4 non è carico, ad es. può essere escluso e lo schema presentato nella condizione del problema può essere semplificato (Fig. b).
Questo circuito è costituito da tre rami paralleli, due dei quali contengono due condensatori in serie.
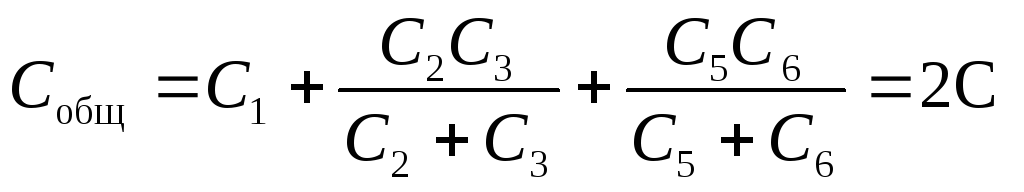
Risposta: C totale = 2 C.
Esempio 12.7. Condensatore ad aria piana con capacità C 1 \u003d 4pF addebitato a una differenza potenzialeu 1 = 100 V. Dopo aver scollegato il condensatore dalla sorgente di tensione, la distanza tra le piastre del condensatore è stata raddoppiata. Determina: 1) differenza di potenzialeu 2 sulle piastre dei condensatori dopo la loro separazione; 2) il lavoro di forze esterne per allontanare le piastre.
Dato: C 1 \u003d 4pF \u003d 4 ∙ 10 -12 F; U 1 \u003d 100 V; d 2 \u003d 2d 1.
Trova: 1) U2 ;2)A.
Soluzione . La carica delle piastre del condensatore dopo la disconnessione dalla sorgente di tensione non cambia, ad es. Q=cost. Ecco perchè
C 1 U 1 \u003d C 2 U 2, (1)
dove C 2 e U 2 sono, rispettivamente, la capacità e la differenza di potenziale sulle piastre dei condensatori dopo che si sono allontanate.
Dato che la capacità di un condensatore piatto 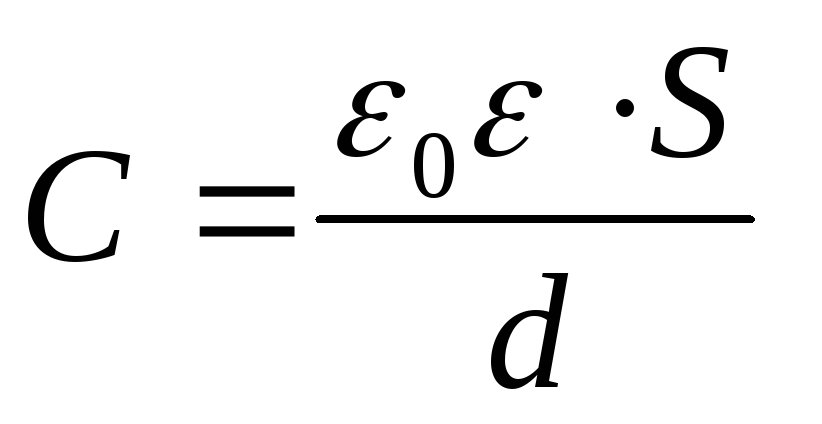 , dalla formula (1) otteniamo la differenza di potenziale desiderata
, dalla formula (1) otteniamo la differenza di potenziale desiderata
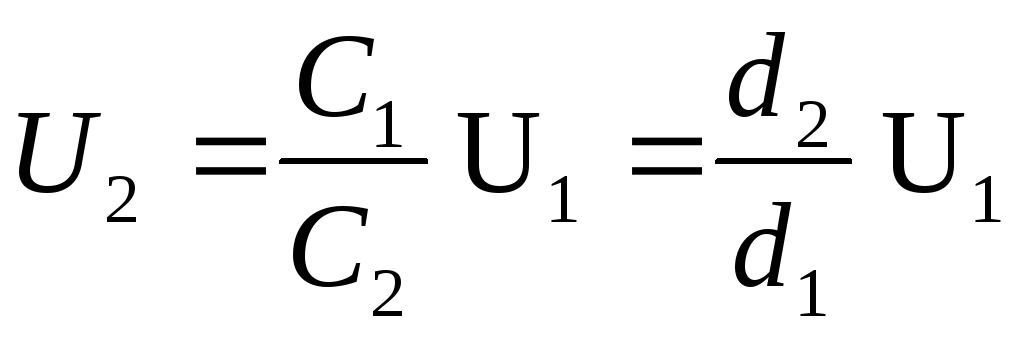 (2)
(2)
Dopo aver scollegato il condensatore dalla sorgente di tensione, il sistema di due piastre cariche può essere considerato chiuso, per il quale è soddisfatta la legge di conservazione dell'energia: il lavoro A delle forze esterne è uguale alla variazione dell'energia del sistema
A \u003d V 2 - V 1 (3)
dove W 1 e W 2 sono l'energia del campo del condensatore rispettivamente nello stato iniziale e finale.
Dato che 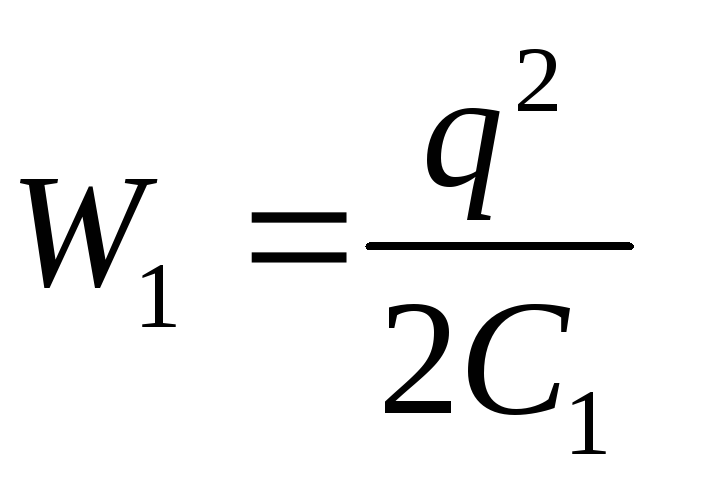 e
e 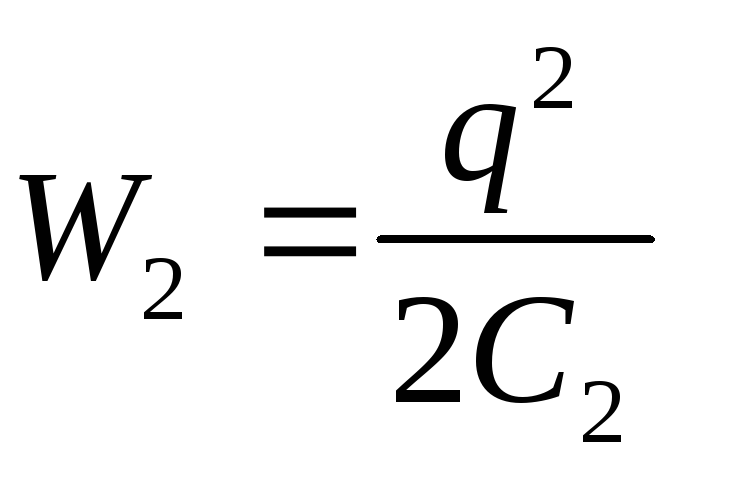 (q – const), dalla formula (3) otteniamo il lavoro desiderato delle forze esterne
(q – const), dalla formula (3) otteniamo il lavoro desiderato delle forze esterne
[tenuto conto che q=C 1 U 1 e formula (2)].
Risposta : 1) U 2 \u003d 200 V; 2) A \u003d 40nJ.
Esempio 12.7. Una sfera solida di dielettrico con un raggioR=5cm caricati uniformemente con densità apparente ρ=5nC/m 3 . Determina l'energia del campo elettrostatico contenuto nello spazio che circonda la palla.
Dato: R=5cm=5∙10 -2 m; ρ=5nC/m 3 = 5∙10 -9 C / m 3.
Trova: w.
Soluzione . Il campo di una palla carica è sfericamente simmetrico, quindi la densità di carica volumetrica è la stessa in tutti i punti situati a distanze uguali dal centro della palla.
e 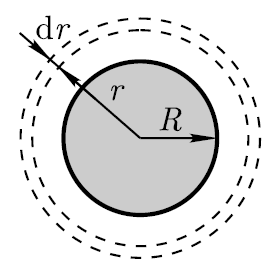 energia in uno strato sferico elementare (viene scelto al di fuori del dielettrico, dove deve essere determinata l'energia) con un volume di dV (vedi figura)
energia in uno strato sferico elementare (viene scelto al di fuori del dielettrico, dove deve essere determinata l'energia) con un volume di dV (vedi figura)
dove dV=4πr 2 dr (r è il raggio di uno strato sferico elementare; dr è il suo spessore); 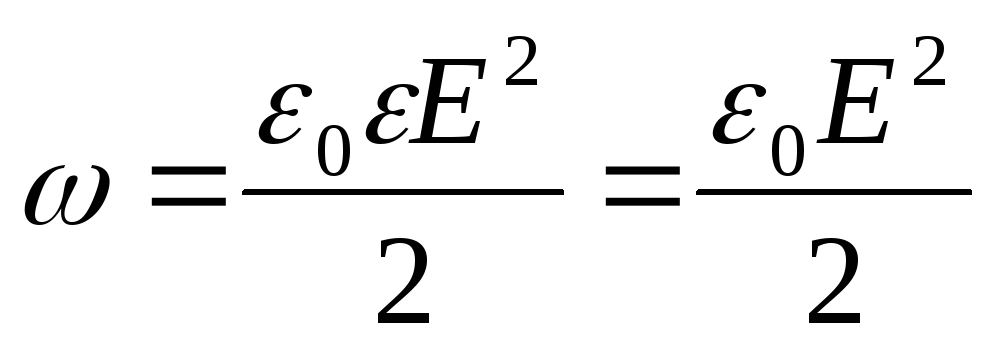 (ε=1 – campo nel vuoto; E – intensità del campo elettrostatico).
(ε=1 – campo nel vuoto; E – intensità del campo elettrostatico).
Troveremo l'intensità E dal teorema di Gauss per un campo nel vuoto, e come superficie chiusa scegliamo mentalmente una sfera di raggio r (vedi figura). In questo caso, l'intera carica della palla, che crea il campo in esame, penetra all'interno della superficie e, secondo il teorema di Gauss,
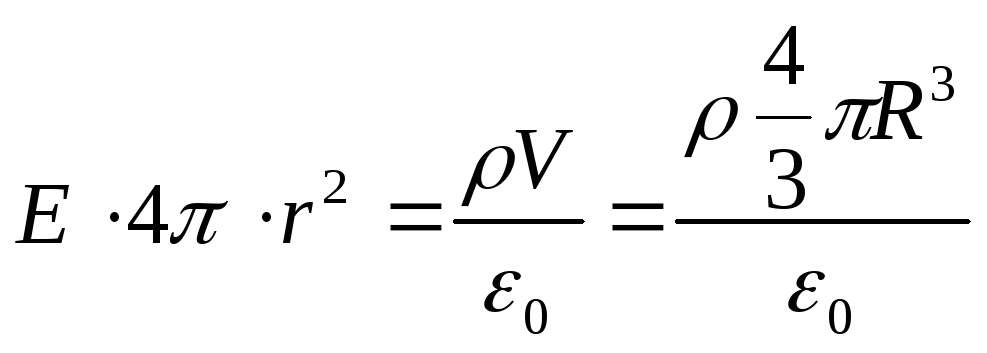
Dove 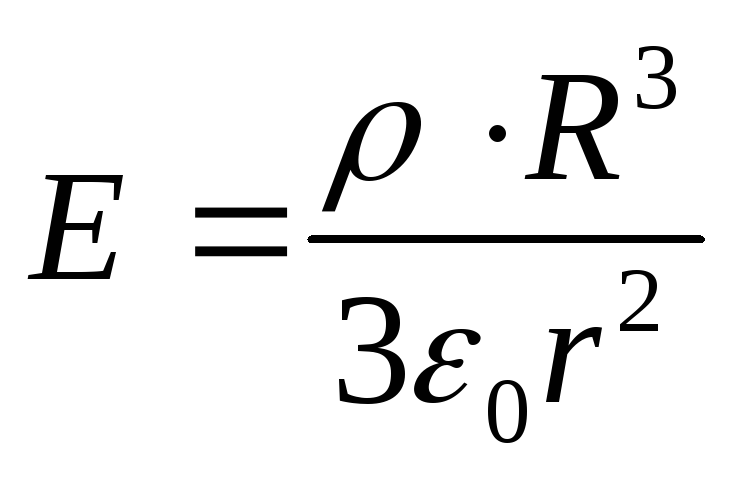
Sostituendo le espressioni trovate nella formula (1), otteniamo
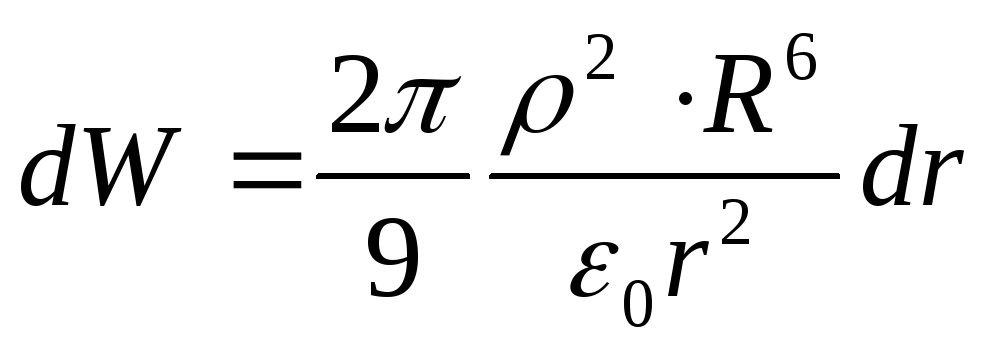
L'energia contenuta nello spazio che circonda la palla,
Risposta: L=6.16∙10 -13 J.
Esempio 12.7. Condensatore planare con l'area delle piastreSe la distanza tra loro ℓ viene riportata la caricaq, dopodiché il condensatore viene scollegato dalla sorgente di tensione. Determina la forza di attrazioneFtra le piastre del condensatore, se la costante dielettrica del mezzo tra le piastre è uguale a ε.
Dato : S; ℓ; q; ε .
Trova: F.
Soluzione . La carica delle piastre del condensatore dopo la disconnessione dalla sorgente di tensione non cambia, ad es. q=cost. Supponiamo che sotto l'azione della forza di attrazione F, la distanza tra le piastre del condensatore sia cambiata di d ℓ . Allora la forza F funziona
Secondo la legge di conservazione dell'energia, questo lavoro è uguale alla perdita di energia del condensatore, ad es.
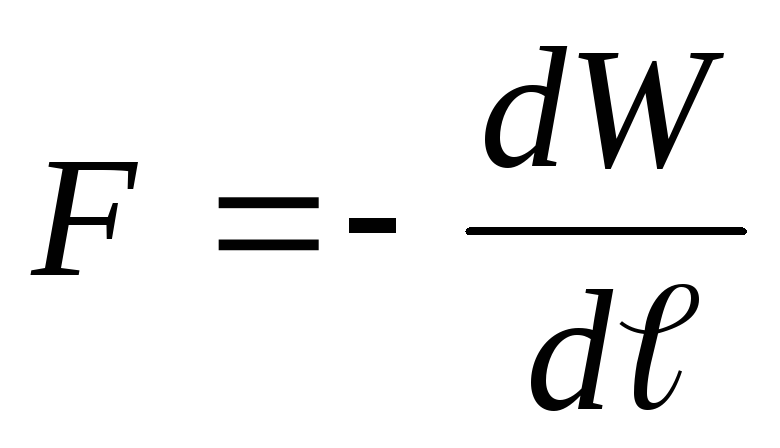 .
(3)
.
(3)
Sostituendo nella formula l'energia di un condensatore carico 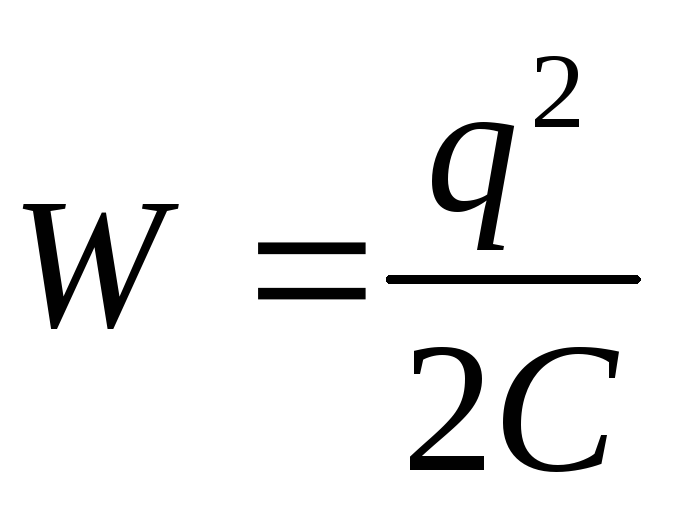 espressione per la capacità di un condensatore piatto
espressione per la capacità di un condensatore piatto 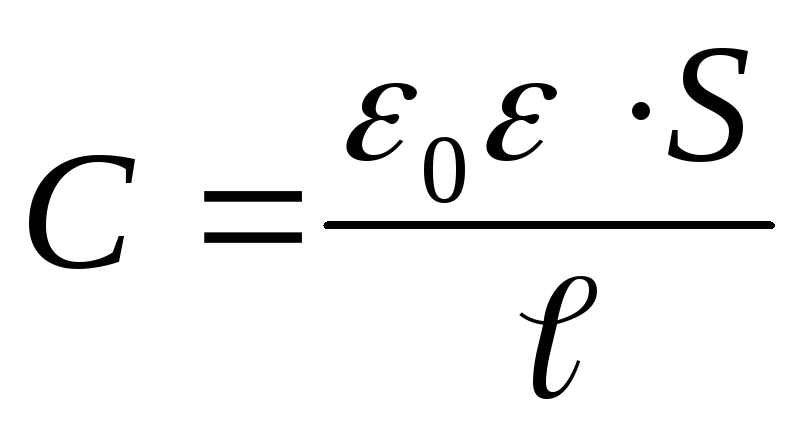 , noi abbiamo
, noi abbiamo
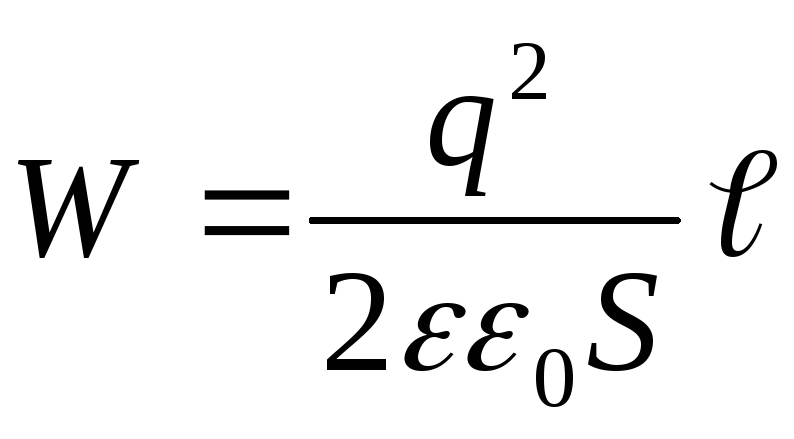 (4)
(4)
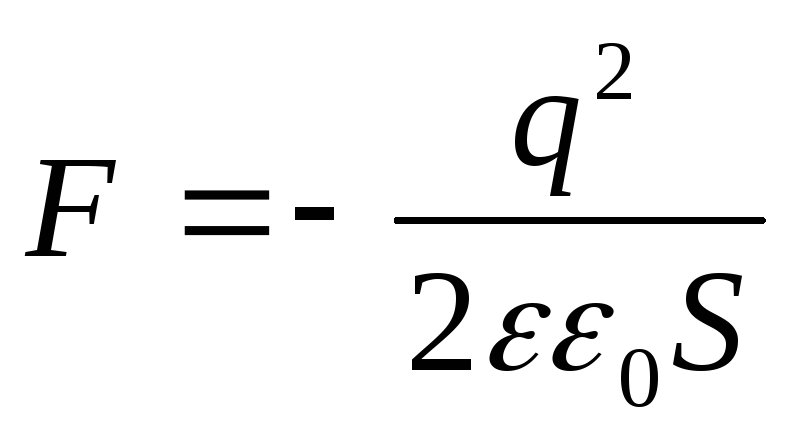
Risposta:
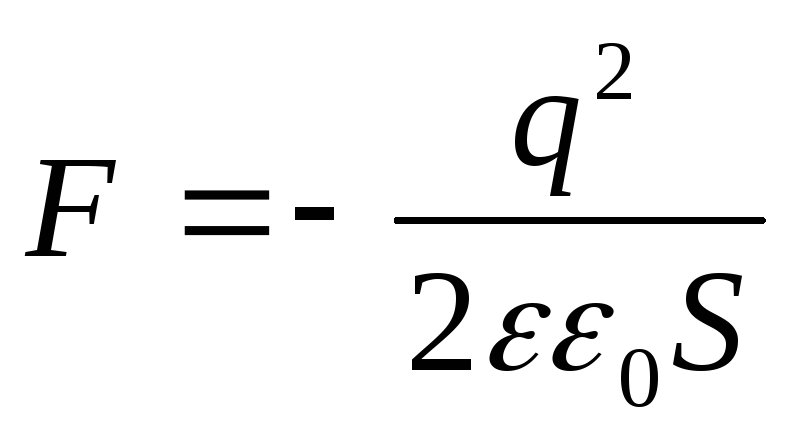
Esempio 12.7. Condensatore piattoSe la distanza tra loro ℓ collegati a una sorgente di tensione costanteu. Determina la forza di attrazioneFtra le piastre del condensatore, se la costante dielettrica del mezzo tra le piastre è uguale a ε.
Dato : S; ℓ; u; ε .
Trova: F.
Soluzione . A seconda della condizione del problema, viene mantenuta una tensione costante sulle piastre del condensatore, ad es. U=cost. Supponiamo che sotto l'azione della forza di attrazione F, la distanza tra le piastre del condensatore sia cambiata di dℓ. Allora la forza F funziona
Secondo la legge di conservazione dell'energia, questo lavoro in questo caso va ad aumentare l'energia del condensatore (confronta con il compito precedente), ad es.
da cui, in base alle espressioni (1) e (2), otteniamo
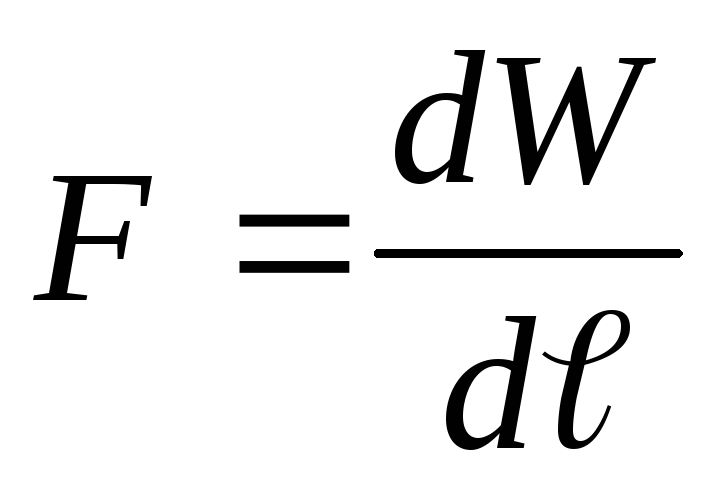 (3)
(3)
Sostituendo nella formula l'energia del condensatore 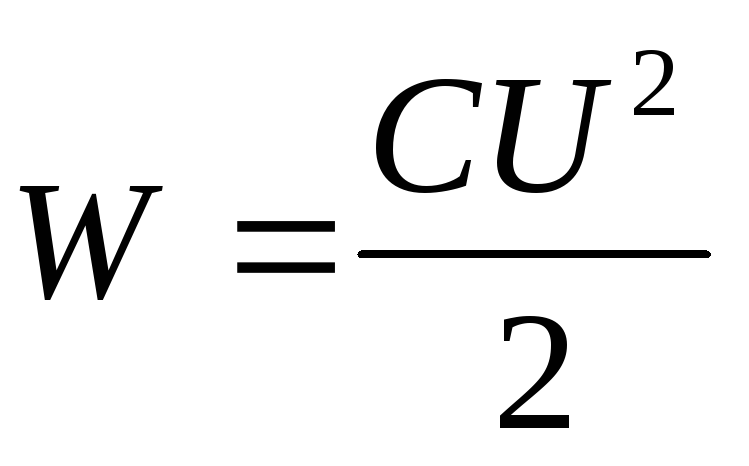 espressione per la capacità di un condensatore piatto
espressione per la capacità di un condensatore piatto  , noi abbiamo
, noi abbiamo
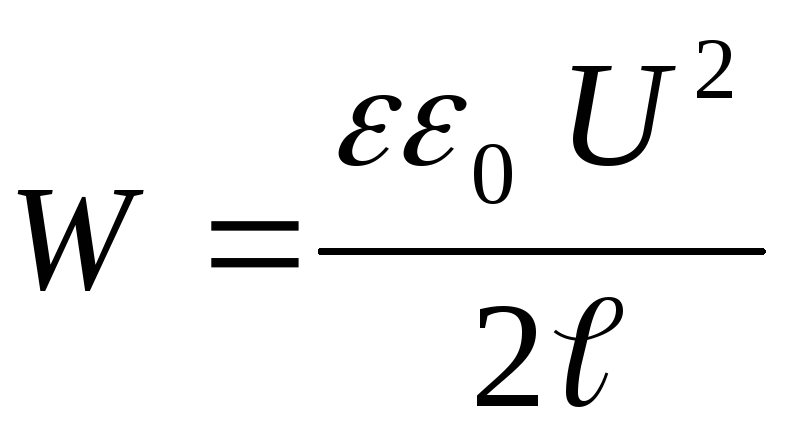 (4)
(4)
Sostituendo il valore di energia (4) nella formula (3) ed effettuando la differenziazione, troviamo la forza di attrazione desiderata tra le piastre del condensatore
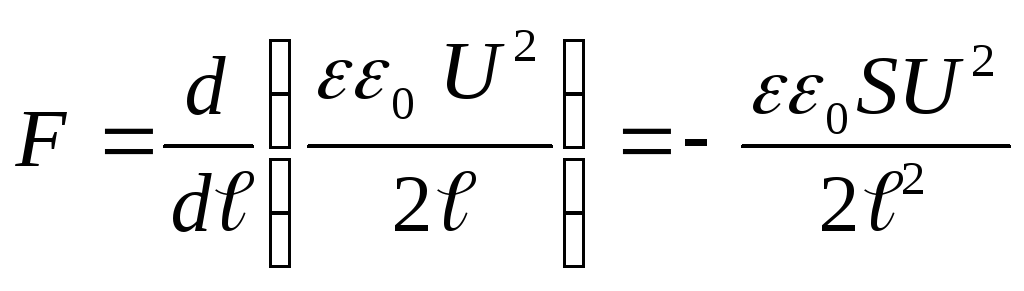 .
.
dove il segno "-" indica che la forza F è una forza attrattiva.
Risposta
: