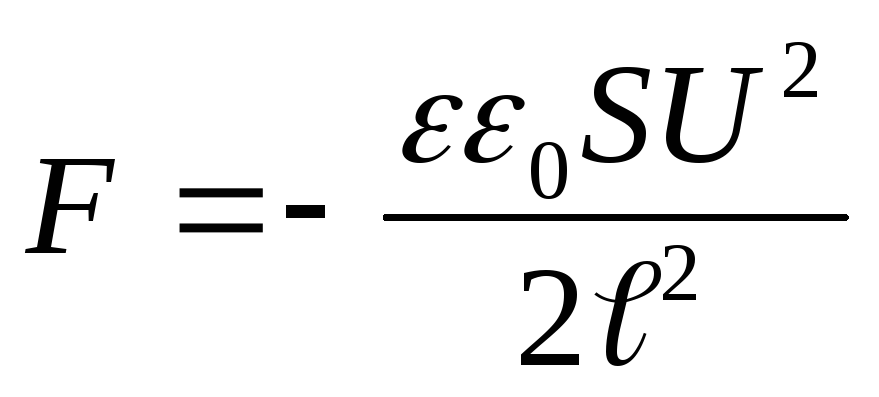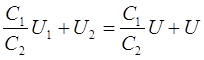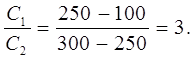Diferența totală de potențial U 0între electrozi este
Calcule:
Răspuns: densitatea de sarcină la suprafață pe plăcile unui condensator
Problema 23
Zona plăcii plată condensator de aer, distanța dintre ele d=5 mm. O diferență de potențial este aplicată plăcilor unui condensator. După ce condensatorul este deconectat de la sursa de tensiune, spațiul dintre plăcile condensatorului este umplut cu ebonită. Care va fi diferența de potențial dintre plăci după umplere? Găsiți capacitățile condensatorului și densitățile de sarcină de suprafață pe plăci înainte și după umplere.
| d
|
| d
|
apoi înainte și după umplere avem
Dat fiind s=constși d=const, primim
![]()
Înainte și după umplerea cu ebonită, avem
![]()
Densitatea sarcinii de suprafață
Calcule:
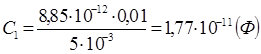
Răspuns: inainte si dupa umplerea cu ebonita avem
Problema 24
Între farfurii condensator plat, situat la distanta d= 1 cm distanta, diferenta de potential aplicata U\u003d 100 V. O placă plană-paralelă de bromură de taliu cristalin () groasă este adiacentă uneia dintre plăci. După deconectarea condensatorului de la sursa de tensiune, placa de cristal este îndepărtată. Care va fi diferența de potențial dintre plăcile condensatorului după aceasta?
putem scrie
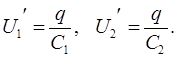
Tensiunea bateriei va fi egală cu suma tensiunilor de pe condensatoarele individuale, adică.
![]()
Prin urmare,
Prin urmare, pentru capacitate DIN din întreaga baterie pe care o găsim
| DIN -q +q d0 e e 01 U 1 |
| С¢ d +q -q e=1 U 2 |
Înlocuind (1) în (2), obținem
Capacitatea condensatorului în a doua poziție
Conform legii conservării sarcinii q=q¢, adică
Calcule:
Răspuns: diferența de potențial va deveni 1,8 kV.
Problema 25
Găsiți capacitate DIN sistemul de condensatori prezentat în figură. Capacitatea fiecărui condensator DIN\u003d 0,5 uF.
| C1 C3 C2 |
găsi C res banca de condensatoare rezultată.
Luați în considerare o baterie și un condensator De la 3, sunt conectate în serie. Știind că la conexiune serială
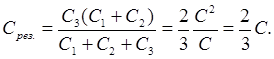
Calcule:
Răspuns: capacitatea sistemului de condensatori este uF.
Problema 26
Capacitatea a doi condensatoare au fost comparate cu un electrometru. Pentru a face acest lucru, ei au fost taxați de diferențe potențiale U 1=300 V și U 2=100 V și a conectat ambii condensatori în paralel. Diferența de potențial măsurată în acest caz între plăcile condensatorului s-a dovedit a fi egală cu U\u003d 250 V. Găsiți raportul capacităților
| A) C1 + - U 1 |
| b) C2
Unde U- diferenta de potential intre placi dupa conectarea lor.
Înlocuirea valorilor q 1 , q 2 , q 1 ¢, q 2 ¢în expresia (1), obținem împarte la DIN 2
Calcule:
Răspuns: raportul condensatorilor Problema 27 Plăci ale unui condensator plat cu o zonă Înlocuiți (2) în (1) și exprimați q Inlocuim expresia (2) in (4), obtinem Înlocuiți (5) în (6) Calcule: |
Semestrul 3. Curs4.
Curs 4. Câmp electric al conductoarelor încărcate.
Energia câmpului electrostatic.
Câmp lângă conductor. Capacitatea conductorilor și a condensatoarelor. (Capacitățile condensatoarelor plate, cilindrice și sferice). Energia unui sistem de sarcini fixe. Energia unui conductor încărcat, condensator. Densitatea energiei câmpului electrostatic.
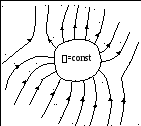
Când un conductor este introdus într-un câmp electric extern, sarcinile din interiorul conductorului încep să se miște sub acțiunea forțelor din câmpul exterior până la atingerea echilibrului. Aceasta duce la o redistribuire a sarcinii electrice în interiorul conductorului. Regiunile conductorului, anterior neutre din punct de vedere electric, capătă o sarcină electrică necompensată. În consecință, un câmp electric apare (sau, după cum se spune, este indus) în conductor  . Condiția pentru echilibrul sarcinilor electrice:
. Condiția pentru echilibrul sarcinilor electrice:
 ,
,
acestea. intensitatea câmpului în interiorul conductorului:
Prin urmare, din egalitate obținem ![]() în interiorul conductorului. Prin urmare, această condiție este îndeplinită și la limita conductorului. Acestea. suprafața conductorului este echipotenţială
suprafaţă
, de aceea linii de forță câmp electric perpendicular pe suprafața conductorului în fiecare punct
.
în interiorul conductorului. Prin urmare, această condiție este îndeplinită și la limita conductorului. Acestea. suprafața conductorului este echipotenţială
suprafaţă
, de aceea linii de forță câmp electric perpendicular pe suprafața conductorului în fiecare punct
.
conductor încărcat .
Dacă o sarcină electrică externă este transmisă unui conductor solitar, atunci condiția pentru echilibrul sarcinilor duce din nou la condiția:
,![]() în interiorul conductorului.
în interiorul conductorului.
Rezultă că toate sarcinile externe sunt situate pe suprafața conductorului, deoarece. intensitatea câmpului din interiorul conductorului este zero și, conform teoremei Gauss, pentru orice suprafață închisă din interiorul conductorului (inclusiv suprafața exterioară a conductorului):
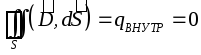 .
.
Deoarece suprafața conductorului în acest caz este și echipotențială, liniile de forță ale câmpului electric sunt direcționate perpendicular pe suprafața conductorului în fiecare dintre punctele sale.
Din teorema lui Gauss rezultă că lângă suprafața conductorului
Mărimea vectorului deplasării electrice este egală cu densitatea suprafeței sarcinilor externe.
Sarcina de pe suprafața conductorului este distribuită astfel încât potențialul de suprafață să rămână constant. Acest lucru duce la faptul că densitatea de sarcină pe suprafața conductorului nu este aceeași. De exemplu, pe părțile ascuțite ale conductorilor, densitatea de sarcină este mai mare decât în adâncituri. În acest sens, apar diverse fenomene, de exemplu, „scărcarea de încărcare”. Dacă conductorul este în aer, atunci ionizarea aerului are loc în apropierea vârfului, ducând o parte din sarcina electrică - un fenomen numit „vânt electric”.
Metoda de imagistică electrică .
Dacă suprafața echipotențială este înlocuită cu una conducătoare și apoi partea din câmp pe care această suprafață o separă este aruncată, atunci modelul câmpului din partea rămasă nu se va schimba. În schimb, dacă imaginea de câmp este completată cu sarcini fictive, astfel încât suprafața conducătoare să poată fi înlocuită cu una echipotențială, atunci imaginea de câmp inițială nu se va modifica.
Exemplu.Aflați forța de atracție a unei sarcini punctiforme către un plan conductor infinit
. Pentru a face acest lucru, vom completa imaginea cu o altă sarcină de același tip, dar de semn opus, situată simetric față de plan. Apoi planul va coincide cu suprafața echipotențială, astfel încât planul poate fi aruncat și forța de interacțiune între sarcini poate fi găsită: 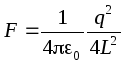 .
.
Energia unui conductor încărcat .
Energia unui conductor solitar încărcat este definită ca energia unui sistem de sarcini: 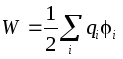 . Pe conductor, deci energia unui conductor solitar:
. Pe conductor, deci energia unui conductor solitar:
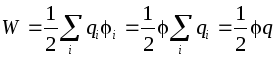 .
.
Pentru un sistem de conductori încărcați: 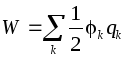 .
.
În special, pentru doi conductori având sarcini q de aceeași mărime, dar cu semn diferit, energia va fi egală cu: 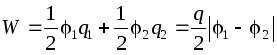 .
.
cometariu
. Mărimea diferenței de potențial ![]() numit Voltaj
între corpuri.
numit Voltaj
între corpuri.
Experiența arată că există o relație liniară între sarcina unui conductor solitar și potențialul acestuia: . Factorul de proporționalitate DIN numit coeficientul electric
containere sau capacitate electrică
.
Unitatea de măsură a capacității electrice este Farad ( 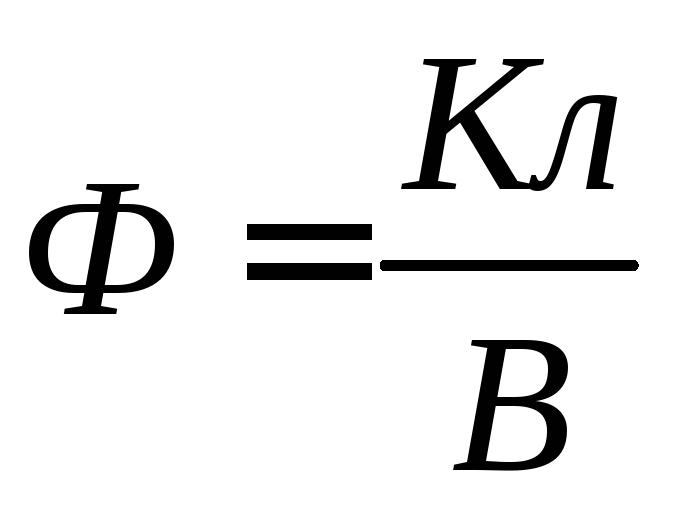 ).
).
Condensator se numește un sistem de doi conductori încărcați cu aceeași mărime, dar diferite ca sarcini de semn. Conductorii sunt numiti plăci de condensator .
Capacitatea unui condensator este determinată de formula.
Condensatorul este desemnat convențional.
Conectarea condensatoarelor
Luați în considerare o conexiune în serie a doi condensatoare C 1 și C 2. Punctul A dintre condensatori este separat de restul circuitului, astfel încât sarcina sa electrică nu se poate modifica. Deoarece sarcina inițială a oricărui punct a fost egală cu zero, atunci ![]() . În consecință, sarcinile plăcilor condensatoarelor adiacente punctului A sunt egale ca mărime, dar semne opuse. Dar, deoarece valoarea încărcăturii plăcilor este egală cu sarcina condensatoarelor, atunci. Sarcina totală a punctului A este zero, așa că dacă aruncăm acest punct împreună cu plăcile, atunci nimic nu se va schimba în circuit. pentru că sarcinile plăcilor extreme sunt, de asemenea, aceleași ca mărime, dar diferite ca semn, atunci condensatorul rezultat va avea aceeași sarcină ca mărime.
. În consecință, sarcinile plăcilor condensatoarelor adiacente punctului A sunt egale ca mărime, dar semne opuse. Dar, deoarece valoarea încărcăturii plăcilor este egală cu sarcina condensatoarelor, atunci. Sarcina totală a punctului A este zero, așa că dacă aruncăm acest punct împreună cu plăcile, atunci nimic nu se va schimba în circuit. pentru că sarcinile plăcilor extreme sunt, de asemenea, aceleași ca mărime, dar diferite ca semn, atunci condensatorul rezultat va avea aceeași sarcină ca mărime.
TOTAL . Sarcinile condensatoarelor conectate în serie sunt de aceeași mărime. Sarcina totală a condensatoarelor conectate în serie este egală cu sarcina fiecăruia dintre condensatori.
În acest caz, tensiunea totală este egală cu suma tensiunilor de pe condensatoare: U GENERAL \u003d U 1 + U 2. Sarcinile condensatoarelor sunt aceleași: q 1 \u003d q 2 \u003d q. Apoi 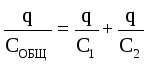 . De aceea
. De aceea 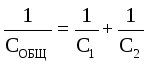 .
.
Când condensatoarele sunt conectate în serie, capacitățile lor sunt adăugate conform legii reciprocelor .
Calculul capacității pentru conectarea în paralel a condensatoarelor.
În acest caz, tensiunile de pe condensatoare sunt aceleași: U 1 \u003d U 2 \u003d U.
Sarcina totală este egală cu suma sarcinilor: q GEN = q 1 + q 2 sau C GEN U=C 1 U+C 2 U.
Atunci C GENERAL =C 1 +C 2 . Când condensatoarele sunt conectate în paralel, capacitățile lor se adună.
Energia condensatorului :
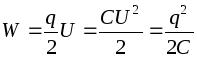 .
.
Sarcina totală a condensatorului este zero. Un condensator stochează energia electrică prin separarea sarcinilor electrice.
Exemple pentru calcularea capacității condensatoarelor .
Condensator plat (aer). reprezintă două plăci paralele, distanţa dintre care este mult mai mică decât dimensiunile plăcilor, astfel încât câmpul dintre plăci poate fi considerat uniform. Există un vid (aer) între plăci, deci = 1.
 În acest caz, atunci când se calculează modelul câmpului, se pot folosi rezultatele obținute pentru câmpul unui plan infinit încărcat. Deoarece sarcinile și ariile plăcilor sunt egale ca mărime, atunci mărimea intensității câmpului creat de fiecare dintre plăci este aceeași: dar direcțiile vectorilor de intensitate sunt diferite (se arată vectorul de intensitate dintr-o placă încărcată negativ). printr-o linie punctată). Între plăci, vectorii de intensitate sunt direcționați în același mod, astfel încât intensitatea totală este egală cu suma intensităților câmpului creat de fiecare dintre plăci:
În acest caz, atunci când se calculează modelul câmpului, se pot folosi rezultatele obținute pentru câmpul unui plan infinit încărcat. Deoarece sarcinile și ariile plăcilor sunt egale ca mărime, atunci mărimea intensității câmpului creat de fiecare dintre plăci este aceeași: dar direcțiile vectorilor de intensitate sunt diferite (se arată vectorul de intensitate dintr-o placă încărcată negativ). printr-o linie punctată). Între plăci, vectorii de intensitate sunt direcționați în același mod, astfel încât intensitatea totală este egală cu suma intensităților câmpului creat de fiecare dintre plăci:
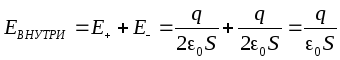 .
.
În afara plăcilor, vectorii intensității câmpului sunt direcționați opus, astfel încât intensitatea câmpului în exterior este zero. În acest fel, într-un condensator, intensitatea câmpului este diferită de zero doar între plăci.
Întrucât câmpul electrostatic este un câmp de forță conservativă, integrala 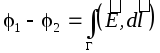 nu depinde de forma traiectoriei G, deci diferența de potențial dintre plăci poate fi găsită de-a lungul perpendicularei care leagă plăcile, a cărei lungime este egală cu d:
nu depinde de forma traiectoriei G, deci diferența de potențial dintre plăci poate fi găsită de-a lungul perpendicularei care leagă plăcile, a cărei lungime este egală cu d: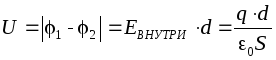 , Unde d este distanța dintre plăci. Apoi, capacitatea unui condensator plat (aer) în conformitate cu definiția va fi egală cu:
, Unde d este distanța dintre plăci. Apoi, capacitatea unui condensator plat (aer) în conformitate cu definiția va fi egală cu: 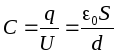
Condensator cilindric (aer). este format din doi cilindri coaxiali
de aceeași lungime, imbricate unele în altele, astfel încât distanța dintre plăci să fie mult mai mică decât dimensiunile plăcilor.
Fie lungimea condensatorului L, sarcina căptușelii interioare este pozitivă: q > 0. Raze de placare R 1 și R 2, lasă R 1 <R 2. Intensitatea câmpului dintre plăci la distanță r de la căptușeala interioară, adică pentru R 1 <r <R 2, găsim folosind teorema Gauss:
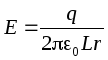 .
.
Apoi tensiunea dintre plăci: .
Prin urmare, capacitatea electrică a unui condensator cilindric (aer): ![]() .
.
DIN  condensator sferic (aer).
reprezintă două sfere concentrice imbricate cu razele plăcilor R 1 și R 2 ,R 1 <R 2. Fie sarcina căptușelii interioare q> 0. Intensitatea câmpului dintre căptușeli la distanță r de la căptușeala interioară ( R 1
<r
<R 2) găsim prin teorema lui Gauss:
condensator sferic (aer).
reprezintă două sfere concentrice imbricate cu razele plăcilor R 1 și R 2 ,R 1 <R 2. Fie sarcina căptușelii interioare q> 0. Intensitatea câmpului dintre căptușeli la distanță r de la căptușeala interioară ( R 1
<r
<R 2) găsim prin teorema lui Gauss:
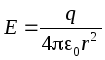 .
.
Tensiune între plăci: .
Prin urmare, capacitatea unui condensator sferic (aer). ![]() .
.
Densitatea energiei volumetrice a câmpului electrostatic.
Luați în considerare un condensator de aer plat. Energia unui condensator încărcat
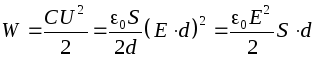 .
.
Cantitatea de spațiu dintre plăcile unui condensator. Deoarece câmpul dintre plăci este considerat a fi omogen, unitatea de volum a acestui câmp are energia 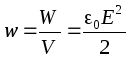 . Această valoare este numită densitatea energiei volumetrice
.
. Această valoare este numită densitatea energiei volumetrice
.
În cazul în care câmpul nu este uniform, densitatea de energie volumetrică este .
În materie, densitatea de energie volumetrică a câmpului electric 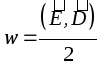 .
.
În cazul unui dielectric izotrop omogen, deci 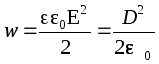 .
.
pentru că ![]() , apoi
, apoi 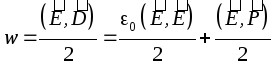 , Unde
, Unde
Energia câmpului electric în vid este energia de polarizare a materiei.
Exemplu . Luați în considerare o sferă încărcată cu pereți subțiri cu raza R. Deoarece sarcinile cu același nume se resping reciproc pe sferă, forțele de respingere au tendința de a întinde suprafața sferei. Putem presupune că din interiorul sferei, pereții sunt afectați de presiune suplimentară p, spargerea sferei și cauzată de prezența unei sarcini electrice la suprafață. Sa gasim R.
Intensitatea câmpului în interiorul sferei este zero, deci densitatea de energie în volum a câmpului electric w este diferit de zero doar în afara sferei.
Cu o ușoară creștere a razei sferei cu dR volumul acestuia va crește, în timp ce în acea parte a spațiului înconjurător care a intrat în interiorul sferei, densitatea volumetrică de energie va deveni egală cu zero. Prin urmare, modificarea energiei câmpului exterior va fi egală cu, unde S este suprafata. Dar odată cu extinderea sferei, forțele de presiune din interiorul sferei vor face treaba ![]() . De atunci
. De atunci ![]() de unde.
de unde.
Exemplu . Să găsim forțele care acționează asupra plăcilor într-un condensator plat încărcat, deconectat de la sursa de alimentare.
Plăcile sunt încărcate opus, așa că se atrag. Să presupunem că plăcile sunt aproape una de cealaltă cu o cantitate mică. X. Apoi volumul condensatorului este redus cu dV = xS, deci energia condensatorului a scăzut cu dW = wdV. Forțele atractive funcționează A = fx. Deoarece A= dW, apoi fx = wxS. Prin urmare, mărimea forței este F = wS. Presiunea suplimentară pe care o creează aceste forţe este egală cu.
Exemplele de mai sus arată că corpurile dintr-un câmp electric sunt supuse unor forțe care provoacă o presiune suplimentară egală cu densitatea energiei volumetrice.
Presiunea cauzată de prezența unui câmp electric este egală cu densitatea de energie volumetrică .
Forțe , acționând asupra corpului din partea unui câmp, se numesc pondemotor .
Plăcile de condensator încărcate opus se atrag reciproc.
Forțele mecanice care acționează asupra corpurilor încărcate macroscopice se numescponderomotiv .
Se calculează forțele ponderomotoare care acționează asupra plăcilor unui condensator plat. În acest caz, sunt posibile două opțiuni:
Condensatorul este încărcat și deconectat de la bateria încărcată(în acest caz, numărul de încărcări de pe plăci rămâne constant q = const).
Când o placă a unui condensator este îndepărtată de cealaltă, munca este gata
datorită căruia energia potențială a sistemului crește:
În acest caz, dA = dW . Echivalând părțile drepte ale acestor expresii, obținem
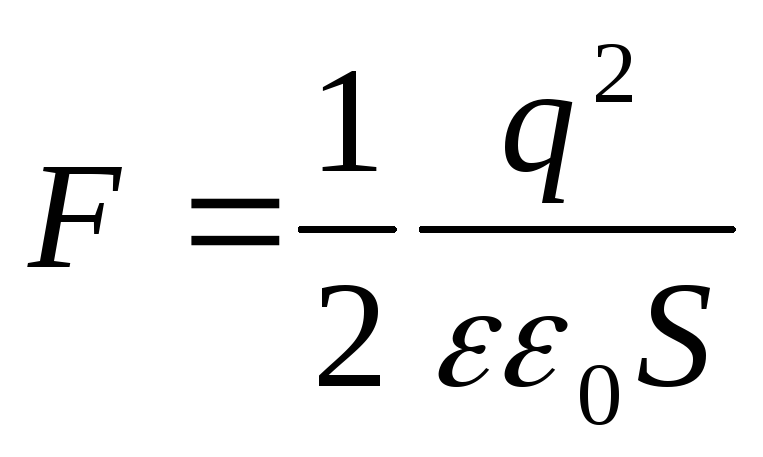 (12.67)
(12.67)
În acest caz, la diferențiere, distanța dintre plăci a fost desemnată x.
Condensator încărcat, dar nu deconectat de la baterie(în acest caz, la mutarea uneia dintre plăcile condensatorului, tensiunea va rămâne constantă ( U = const). În acest caz, atunci când o placă se îndepărtează de cealaltă, energia potențială a câmpului condensatorului scade, deoarece sarcinile „scurg” din plăci, prin urmare
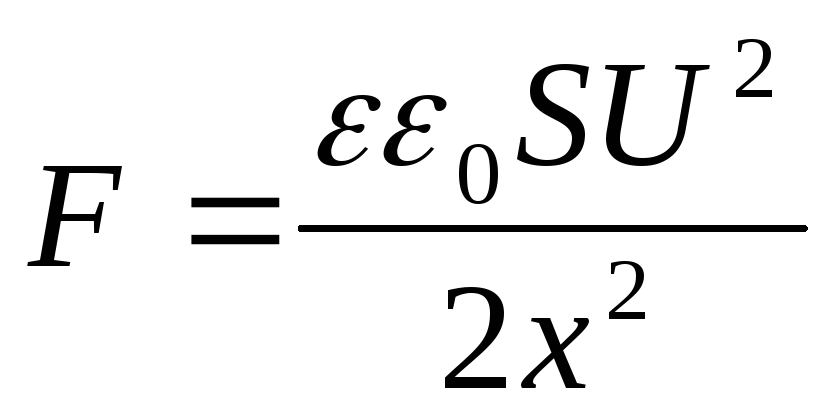
Dar 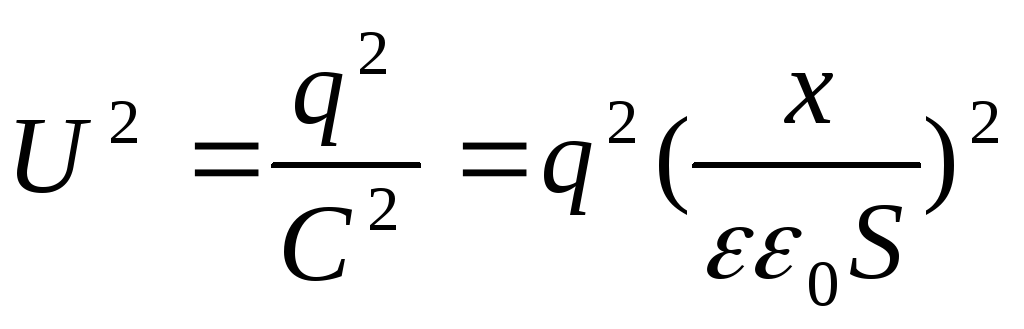 , apoi
, apoi
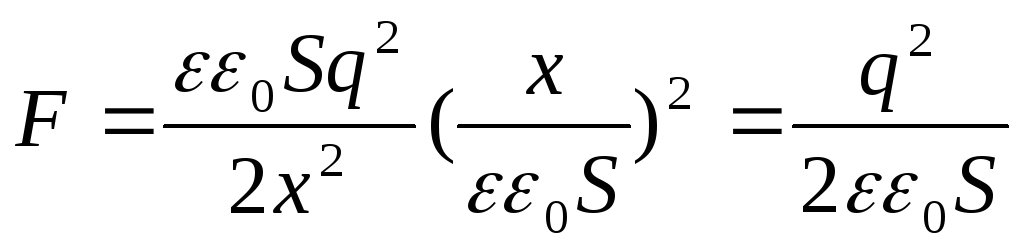
Expresia rezultată coincide cu formula 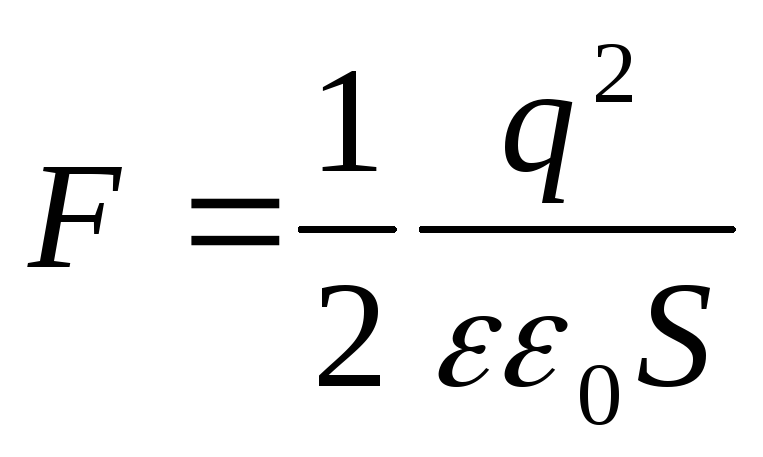 . Poate fi reprezentat și sub altă formă dacă în locul sarcinii q introducem densitatea suprafeței:
. Poate fi reprezentat și sub altă formă dacă în locul sarcinii q introducem densitatea suprafeței:
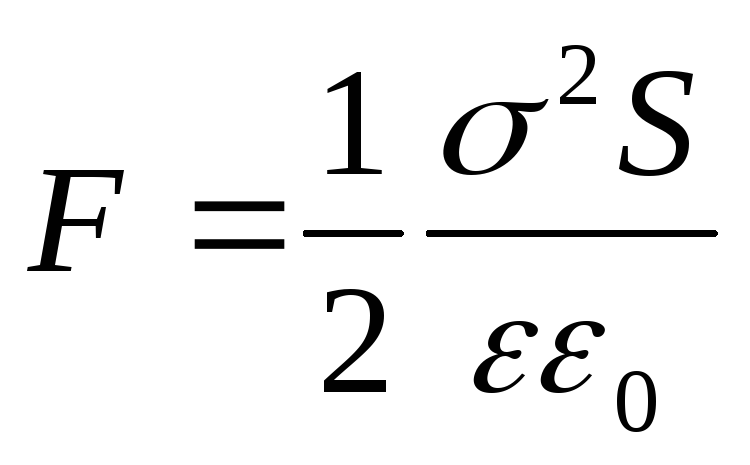 (12.68)
(12.68)
Câmpul este uniform. Intensitatea câmpului condensatorului este 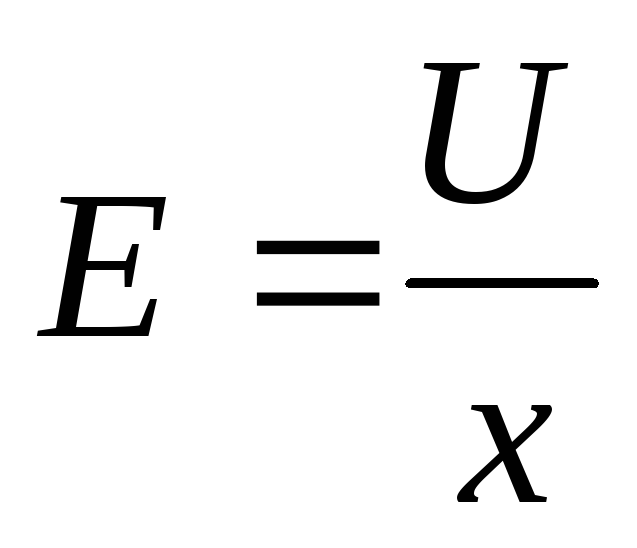 , unde x este distanța dintre plăci. Înlocuind în formulă
, unde x este distanța dintre plăci. Înlocuind în formulă 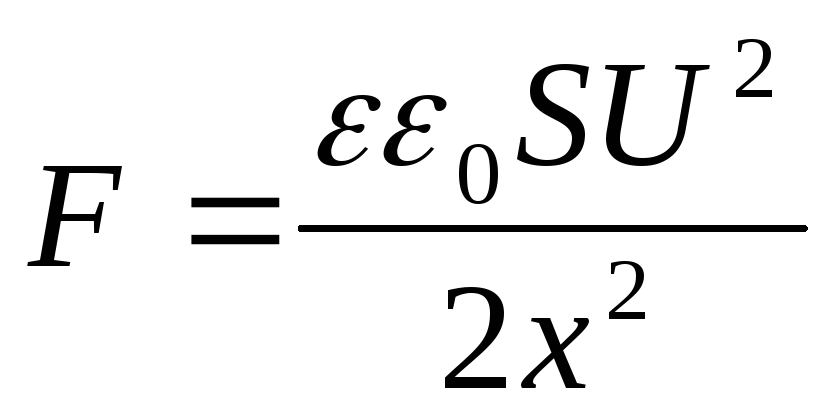 U 2 \u003d E 2 x 2, obținem că forța de atracție a plăcilor unui condensator plat
U 2 \u003d E 2 x 2, obținem că forța de atracție a plăcilor unui condensator plat
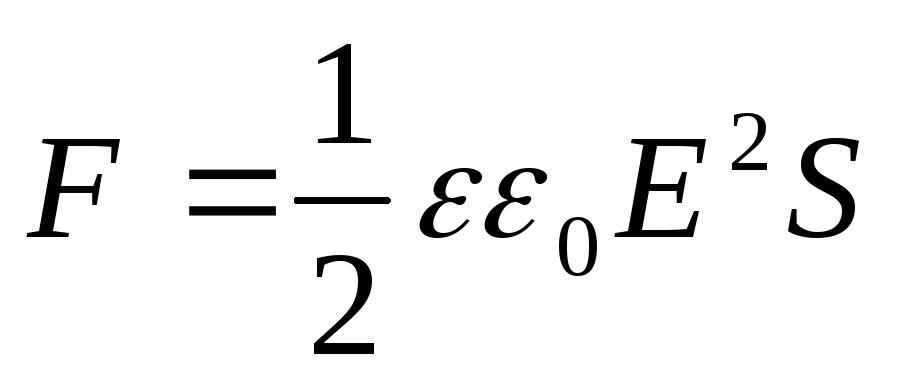 (12.69)
(12.69)
Aceste forțe acționează nu numai asupra plăcilor. Deoarece plăcile, la rândul lor, pun presiune asupra dielectricului plasat între ele și îl deformează, apare presiune în dielectric.
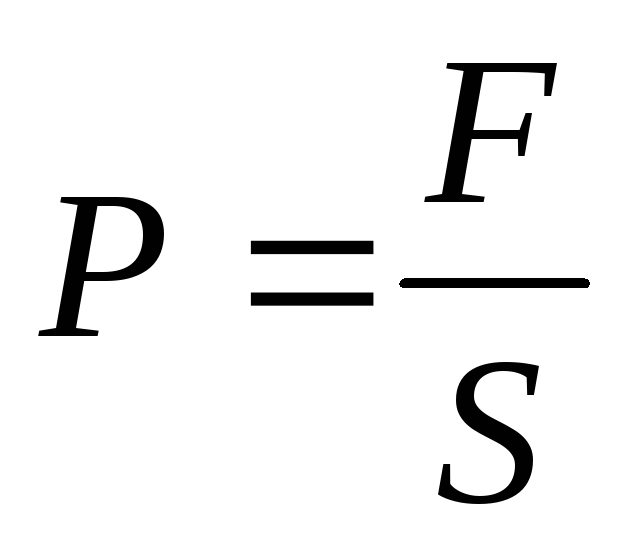
(S este aria fiecărei plăci).
Presiunea care apare în dielectric este
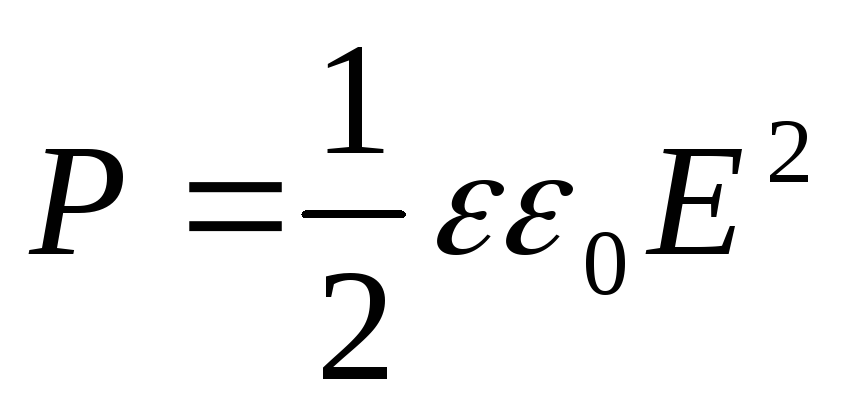 (12.70)
(12.70)
Exemple de rezolvare a problemelor
Exemplul 12.5. O diferență de potențial de 1,5 kV este aplicată plăcilor unui condensator de aer plat. Suprafata farfurii 150 cm 2 iar distanța dintre ele este de 5 mm. După deconectarea condensatorului de la sursa de tensiune, sticlă a fost introdusă în spațiul dintre plăci (ε 2 =7). Definiți:
1) diferența de potențial dintre plăci după introducerea unui dielectric; 2) capacitatea condensatorului înainte și după introducerea dielectricului; 3) densitatea de sarcină de suprafață pe plăci înainte și după introducerea dielectricului.
Dat: U 1 \u003d 1,5 kV \u003d 1,5 ∙ 10 3 V; S \u003d 150cm 2 \u003d 1,5 ∙ 10 -2 m 2; ε 1 =1; d=5mm=5∙10 -3 m.
Găsiți: 1) U2; 2) C1C2; 3) σ 1 , σ 2
Soluţie
.
pentru că 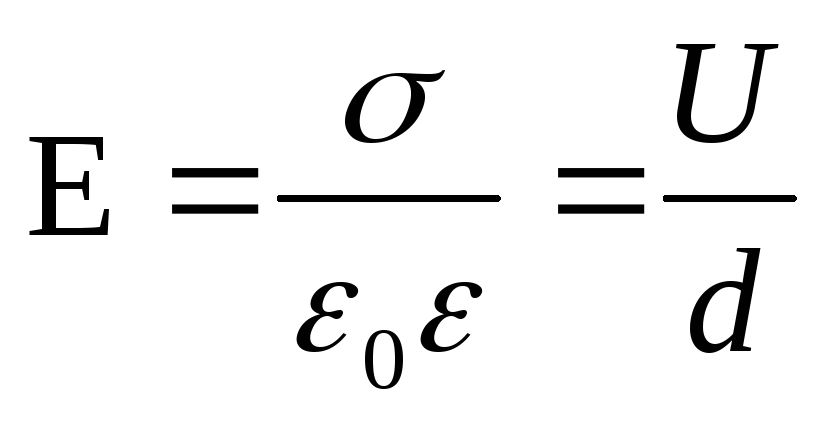 (σ este densitatea de sarcină la suprafață pe plăcile condensatorului), apoi înainte de introducerea dielectricului σd=U 1 ε 0 ε 1 și după introducerea dielectricului σd=U 2 ε 0 ε 2, deci
(σ este densitatea de sarcină la suprafață pe plăcile condensatorului), apoi înainte de introducerea dielectricului σd=U 1 ε 0 ε 1 și după introducerea dielectricului σd=U 2 ε 0 ε 2, deci
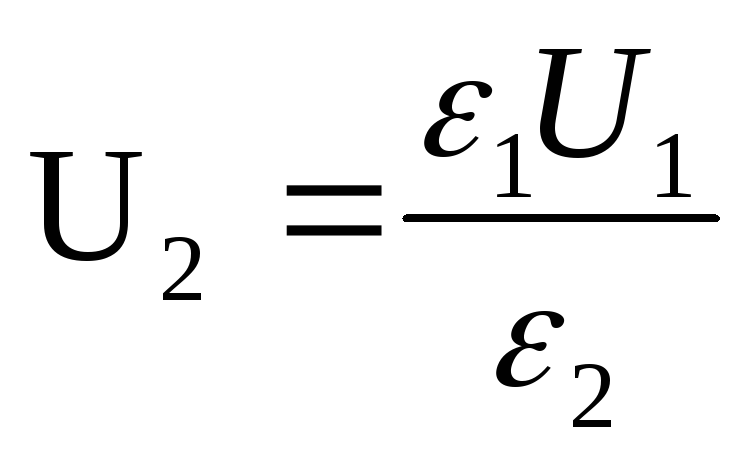
Capacitatea condensatorului înainte și după introducerea unui dielectric
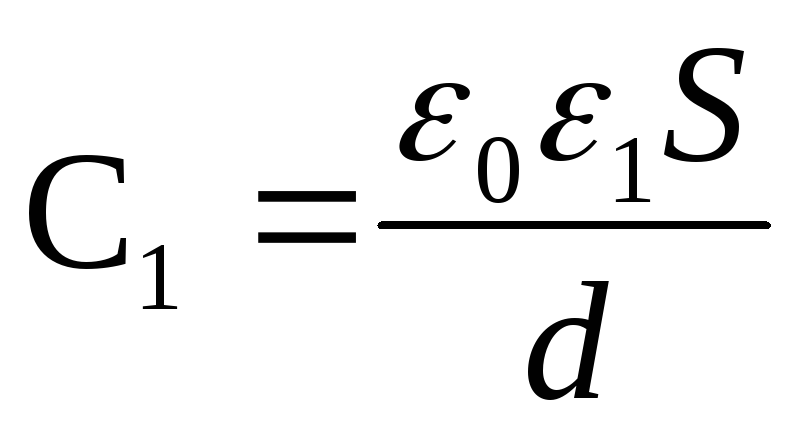 și
și 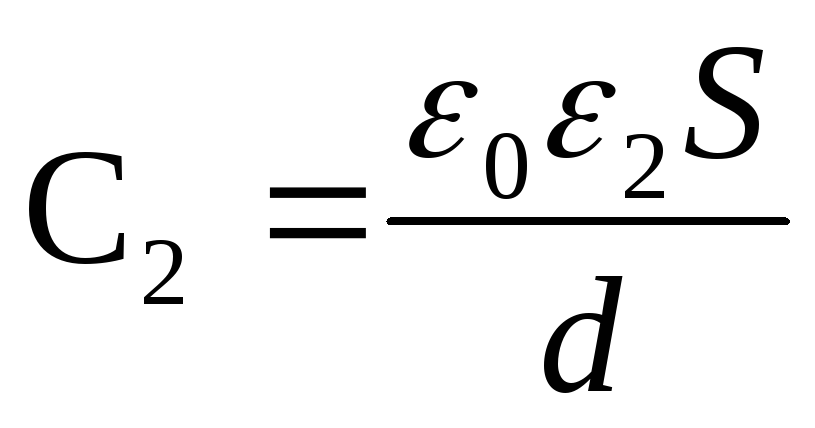
Încărcarea plăcilor după deconectarea de la sursa de tensiune nu se modifică, adică. q=const. Prin urmare, densitatea de sarcină de suprafață pe plăci înainte și după introducerea dielectricului
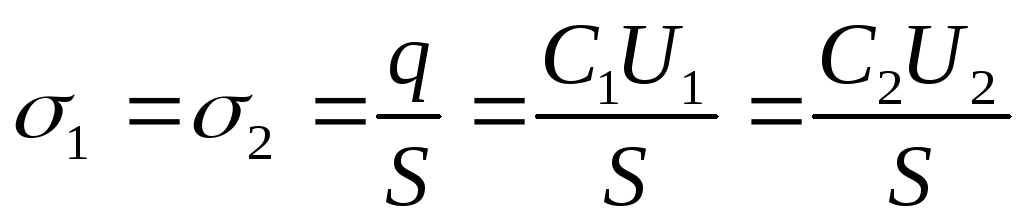
Răspuns: 1) U 2 \u003d 214V; 2) C 1 \u003d 26,5 pF; C 2 \u003d 186pF; 3) σ 1 = σ 2 = 2,65 μC/m 2.
Exemplul 12.7. Spațiul dintre plăcile unui condensator plat este umplut cu un dielectric anizotrop, a cărui permeabilitate ε variază în direcția perpendiculară pe plăci conform legii liniare.ε = α + βх de la ε 1 până la ε 2 , și ε 2 > ε 1 . Zona fiecărei căptușeliS, distanța dintre eled. Aflați capacitatea condensatorului.
Dat:S; d; ε1; ε 2
Găsi: DIN.
Soluţie
.
Constanta dielectrică ε
variază liniar, ε = α + βx, unde x este măsurat de la căptușeală, a cărei permeabilitate este egală cu ε 1 . Considerând că ε (0) = ε 1 , ε (d) = ε 2 , obținem dependența 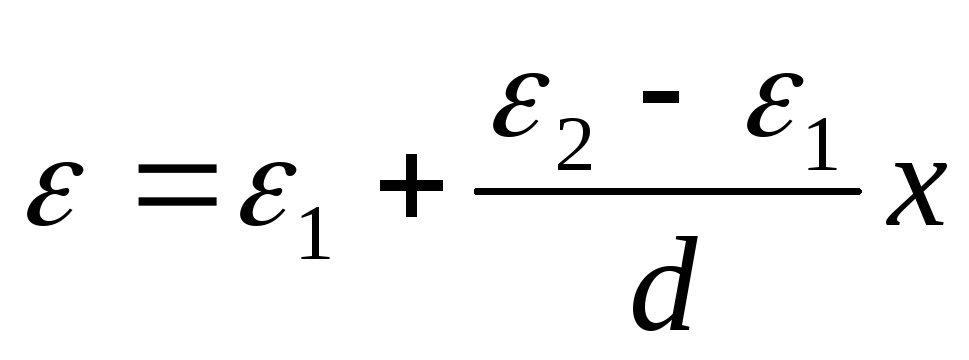 . Găsiți diferența de potențial dintre plăci:
. Găsiți diferența de potențial dintre plăci:
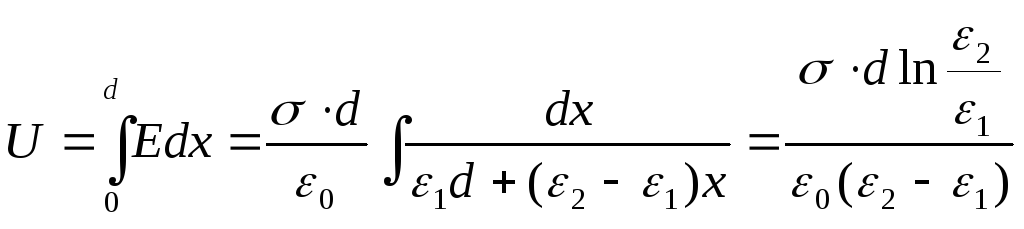
Capacitatea condensatorului va fi
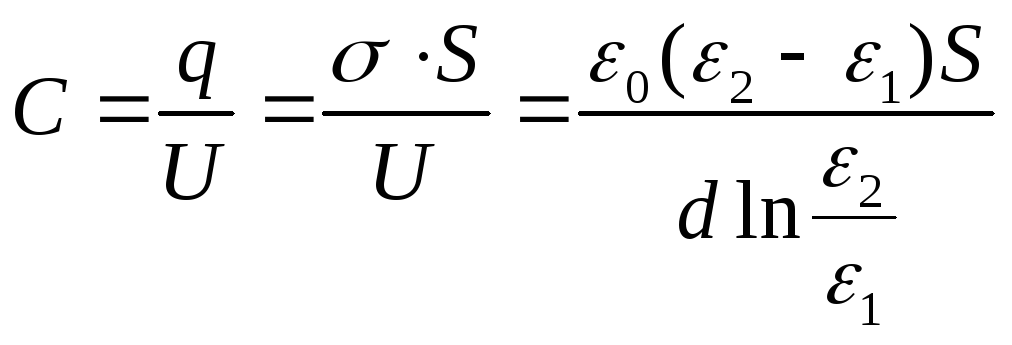
Răspuns:
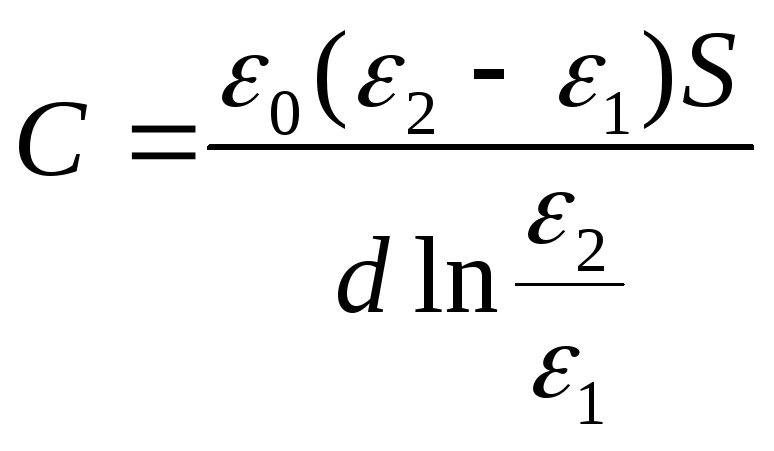
Exemplul 12.7. Între plăcile unui condensator plat încărcat la o diferență de potențial U , două straturi de dielectrici sunt așezate paralel cu plăcile sale. Grosimea straturilor și, respectiv, permitivitatea dielectricilor sunt,d 1 , d 2 , ε 1 , ε 2 . Determinați puterea câmpurilor electrostatice în straturile dielectrice.
Dat: U; d 1 , d 2 , ε 1 , ε 2
Găsi: E1, E2.
Soluţie . Tensiunea pe plăcile condensatorului, având în vedere că câmpul din fiecare dintre straturile dielectrice este uniform,
U=E 1 d 1 + E 2 d 2 . (unu)
Deplasarea electrică în ambele straturi dielectrice este aceeași, așa că putem scrie
D=D1=D2= ε 0 ε 1 E 1 = ε 0 ε 2 E 2 (2)
Din expresiile (1) și (2) găsim cel dorit
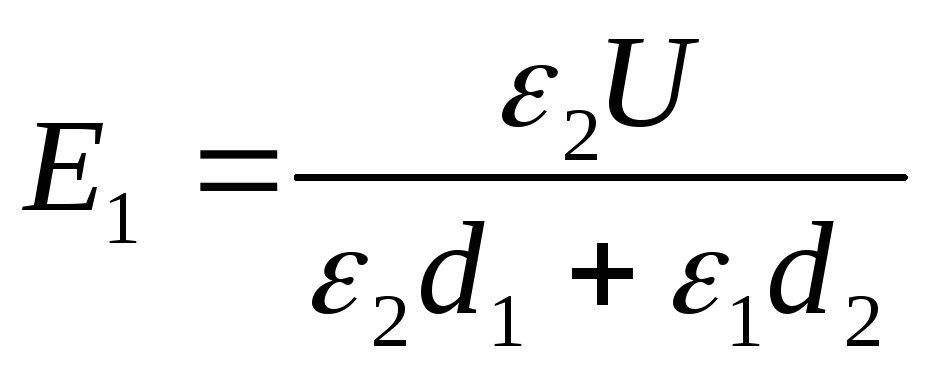 (3)
(3)
Din formula (2) rezultă că
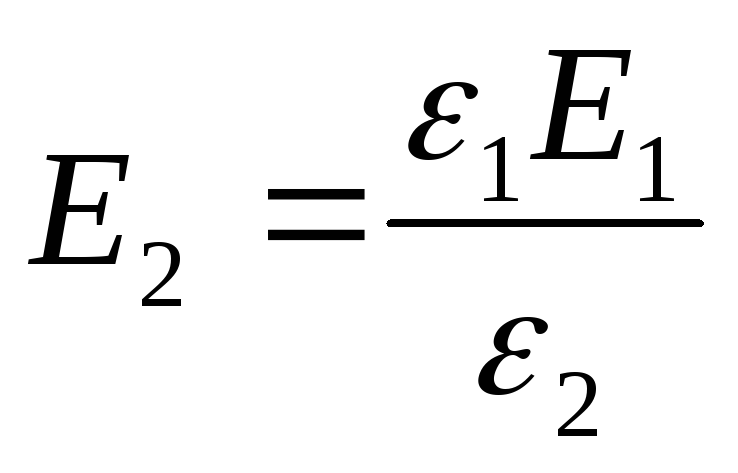
Răspuns:
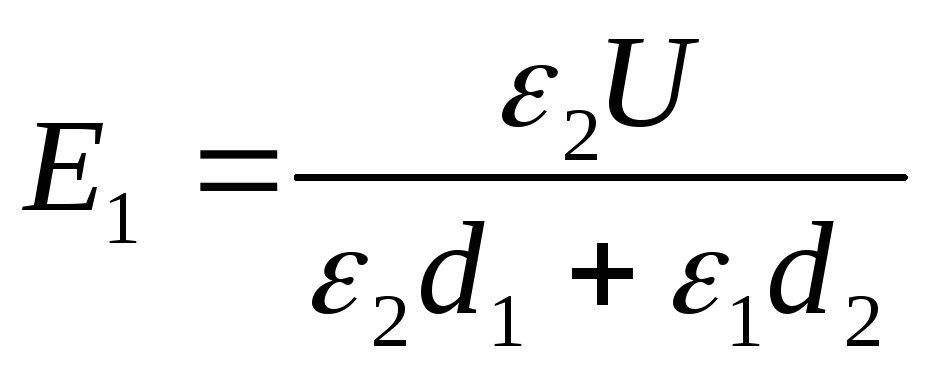 ;
;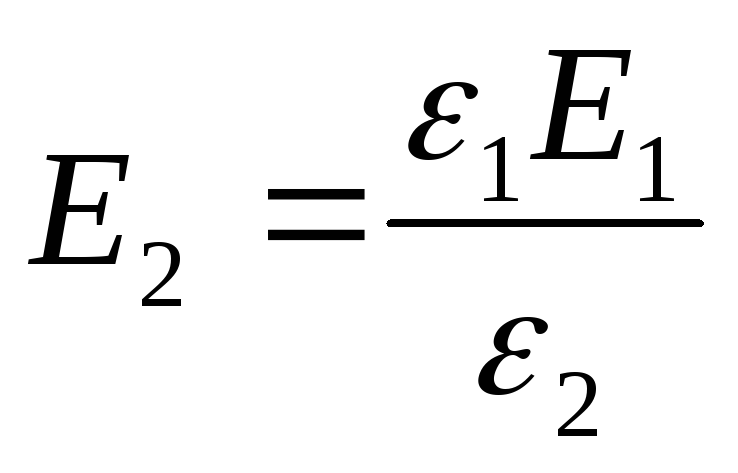
Exemplul 12.7. Zona farfurii S condensatorul plat este de 100 cm 2 . Spațiul dintre plăci este umplut îndeaproape cu două straturi de dielectrici - o placă de mică (ε 1 =7) gros d 1 =3,5 mm și parafină (ε 2 =2) grosime d 2 =5 mm. Determinați capacitatea acestui condensator.
Dat: S= 100 cm 2 =10 -2 m 2 ; ε 1 =7; d 1 =3,5mm=3,5∙10 -3 m;, ε 1 =2; d 1 =3,5mm=5∙10 -3 m;
Găsi: DIN.
Soluţie . Capacitatea condensatorului
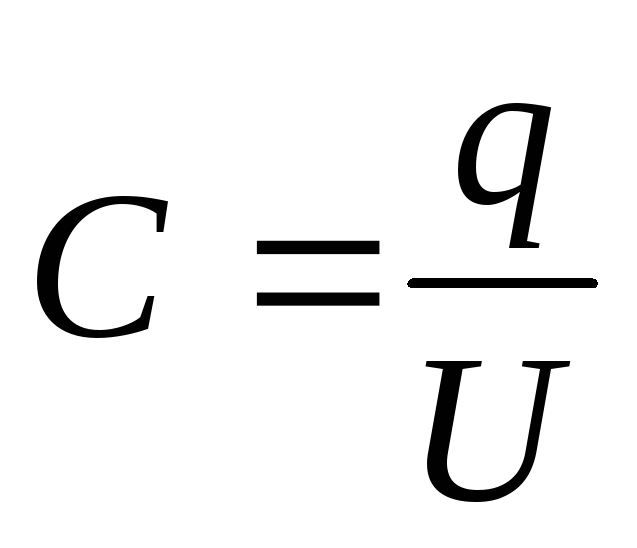
unde = - sarcina pe placile condensatorului (- densitatea sarcinii la suprafata pe placi); \u003d - diferența de potențial a plăcilor, egală cu suma tensiunilor de pe straturile dielectrice: U \u003d U 1 +U 2. Apoi
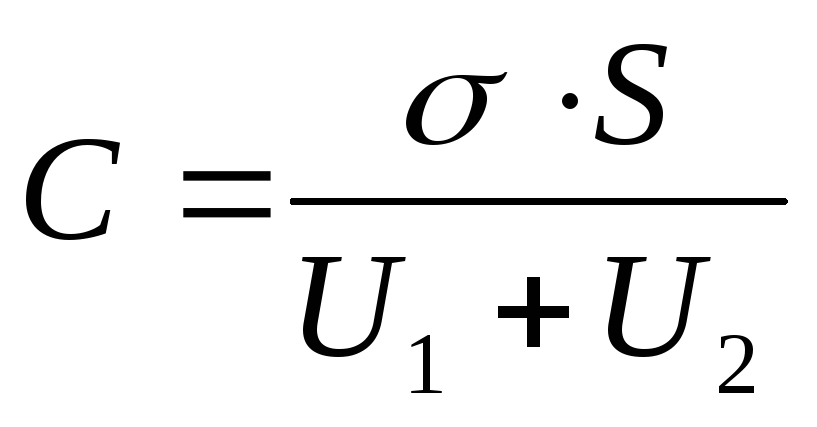 (1)
(1)
Tensiunile U 1 și U 2 se găsesc prin formule
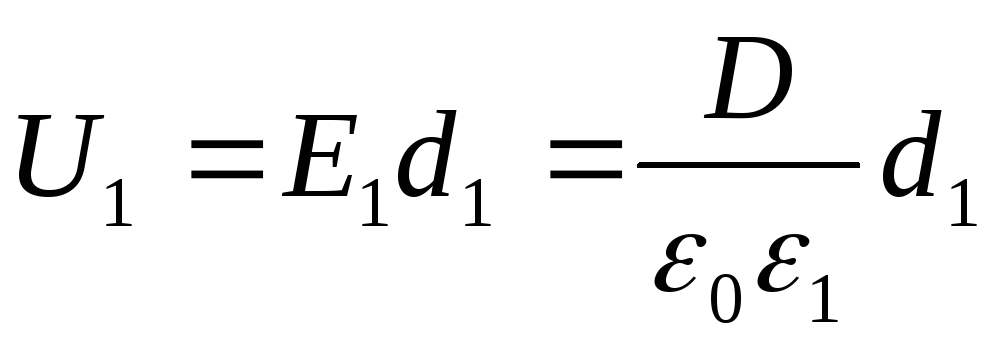 ;
;
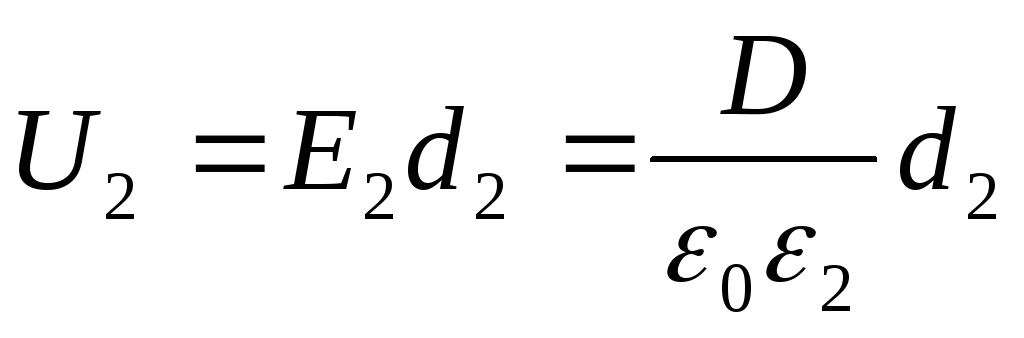 (2)
(2)
unde E 1 și E 2 - intensitatea câmpului electrostatic în primul și al doilea strat al dielectricului; D este deplasarea electrică în dielectrici (la fel în ambele cazuri). Ținând cont de faptul că
Și având formula (2), din expresia (1) găsim capacitatea dorită a condensatorului
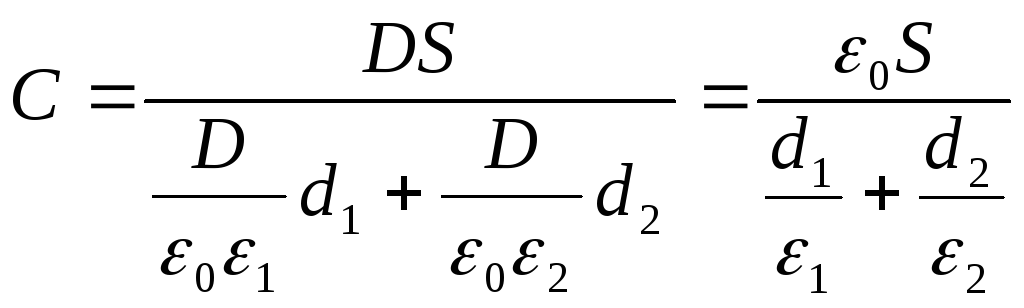
Răspuns: C \u003d 29,5pF.
Exemplul 12.7. O baterie cu trei condensatoare conectate în seria C 1 \u003d 1 μF; DIN 2 \u003d 2uF și C 3 \u003d 4 μF sunt conectate la o sursă EMF. Încărcarea bateriei condensatorului q \u003d 40 μC. Determinați: 1) tensiunea U 1 , U 2 și U 3 pe fiecare condensator; 2) sursa EMF; 3) capacitatea bancului de condensatori.
Dat : C 1 \u003d 1 μF \u003d 1 ∙ 10 -6 F; C 2 \u003d 2 μF \u003d 2 ∙ 10 -6 F și C 3 \u003d 4 μF \u003d 4 ∙ 10 -6 F; q \u003d 40 μC \u003d 40 ∙ 10 -6 F .
Găsiți: 1) U1, U2, U3 ; 2) ξ; 3) C.
Soluţie . Atunci când condensatoarele sunt conectate în serie, sarcinile tuturor plăcilor sunt egale în valoare absolută, prin urmare
q 1 \u003d q 2 \u003d q 3 \u003d q.
Tensiunea condensatorului
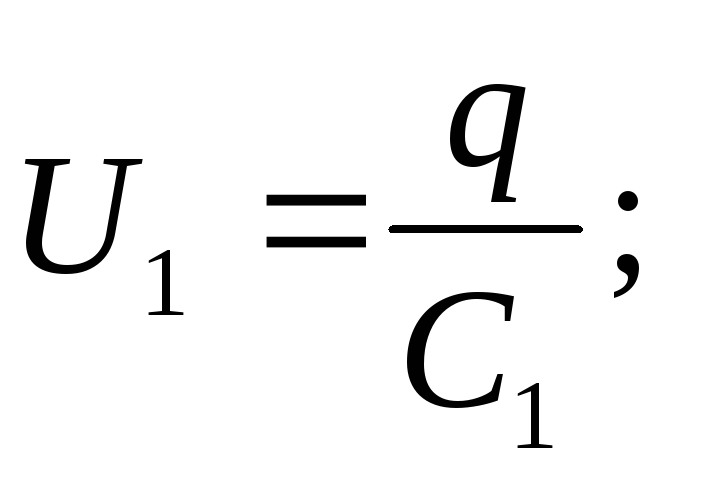
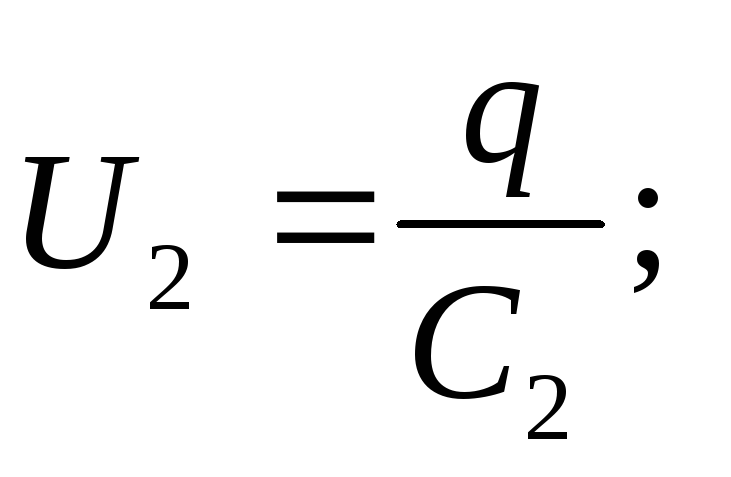
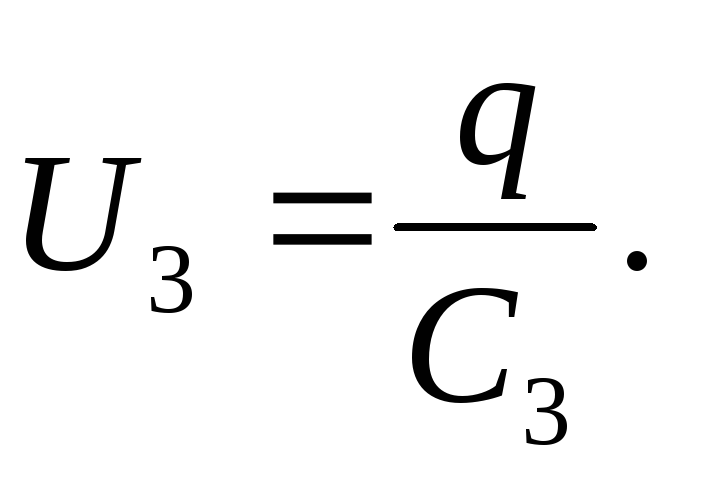
EMF-ul sursei este egal cu suma tensiunilor fiecăruia dintre condensatoarele conectate în serie:
ξ \u003d U 1 + U 2 + U 3
Când sunt conectate în serie, inversele capacităților fiecăruia dintre condensatori sunt însumate:
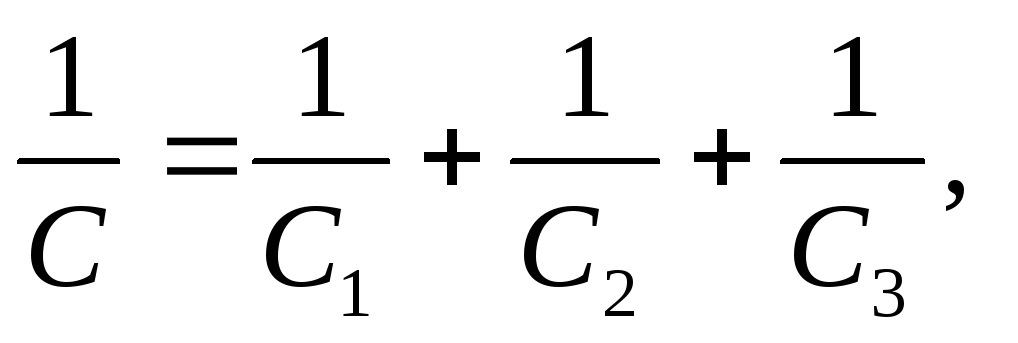
Unde este capacitatea dorită a băncii de condensatoare
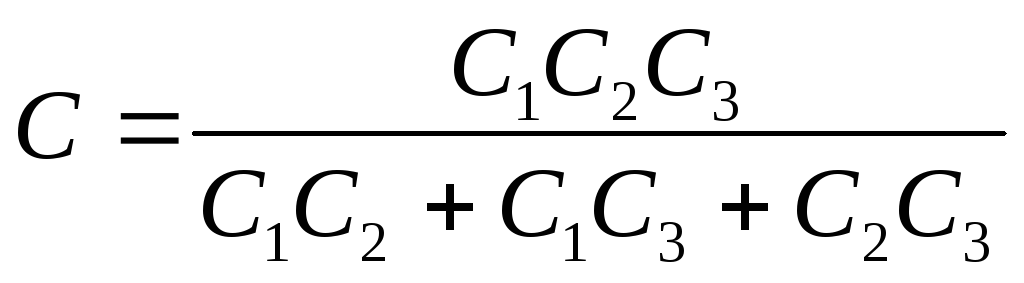
Raspunsul 1) U 1 \u003d 40V; U 2 \u003d 20V, U 3 = 10V; 2) Ɛ= 70V; 3) C \u003d 0,571 μF.
Exemplul 12.7. Două condensatoare de aer plat de aceeași capacitate sunt conectate în serie și conectate la o sursă EMF. De câte ori și de câte ori se va schimba sarcina condensatoarelor dacă unul dintre ei este scufundat în ulei cu o constantă dielectrică ε=2,2.
Dat: C 1 \u003d C 2 \u003d C; q \u003d 40 μC \u003d 40 ∙ 10 -6 F ; ε 1 =1; ε 2 =2,2.
Găsi:
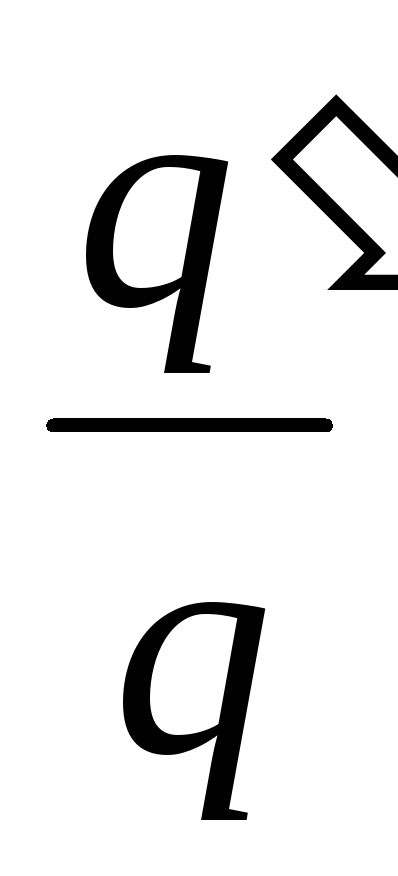 .
.
Soluţie . Când condensatoarele sunt conectate în serie, încărcările ambelor condensatoare sunt egale ca mărime. Înainte de scufundare într-un dielectric (în ulei), încărcarea fiecărui condensator
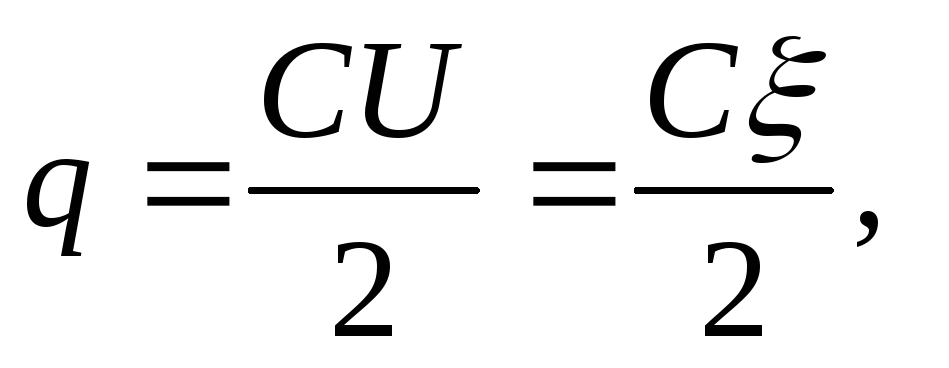
unde ξ \u003d U 1 + U 2 (când condensatorii sunt conectați în serie, EMF-ul sursei este egal cu suma tensiunilor fiecărui condensator).
După ce unul dintre condensatori este scufundat într-un dielectric, sarcinile condensatoarelor sunt din nou aceleași și, respectiv, pe primul și al doilea condensator sunt egale.
q= CU 1 =ε 2 CU 2
(ținând cont că ε 1 =1), de unde, dacă ținem cont că ξ = U 1 + U 2 , aflăm
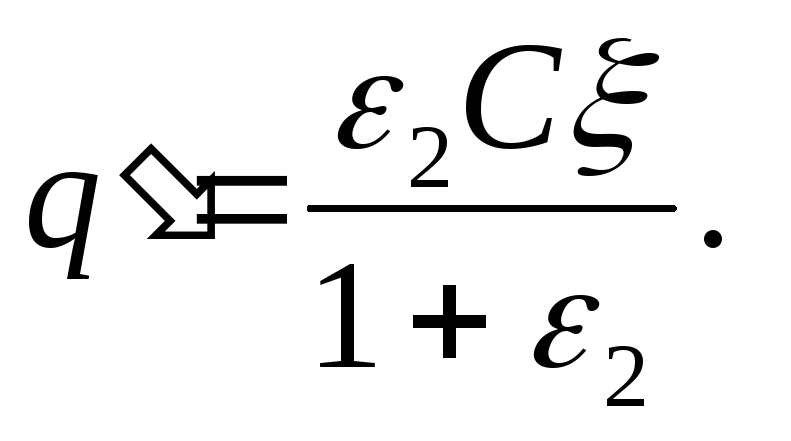 (2)
(2)
Împărțind (2) la (1), găsim raportul dorit
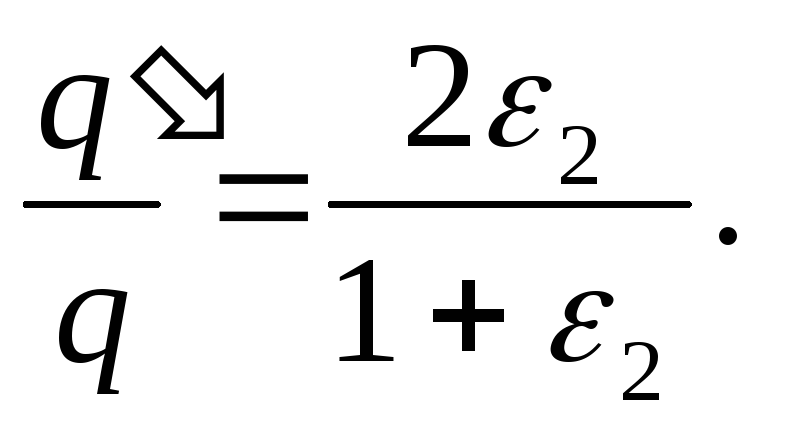
Răspuns:
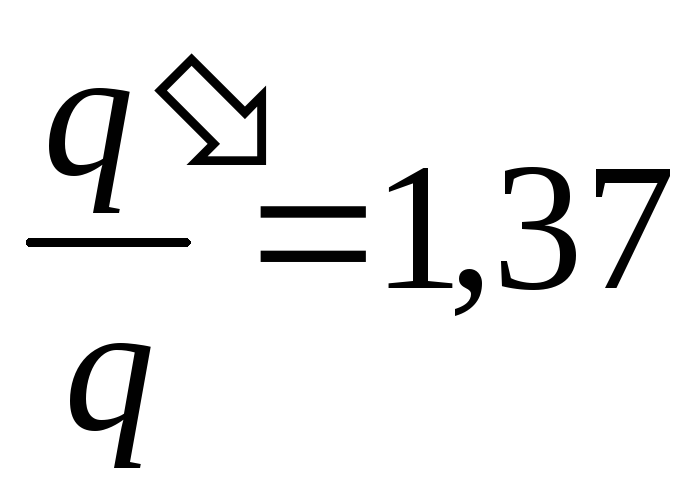 , adică sarcina condensatoarelor crește cu un factor de 1,37.
, adică sarcina condensatoarelor crește cu un factor de 1,37.
Exemplul 12.7. Condensatoarele cu capacități C fiecare sunt conectate așa cum se arată în fig.a. determina capacitatea uzual această conexiune a condensatoarelor. .
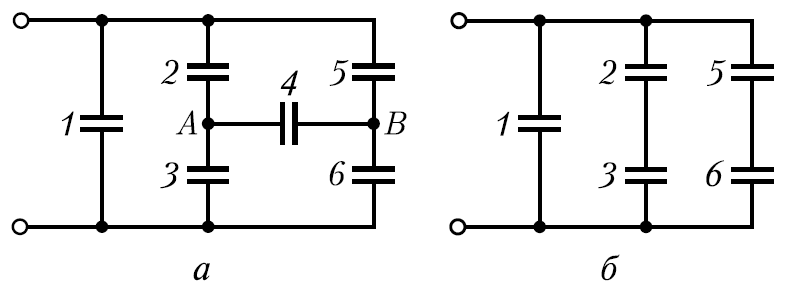 Soluţie
.
Dacă deconectați condensatorul C 4 de la circuit, obțineți o conexiune a condensatoarelor, care este ușor de calculat. Deoarece capacitățile tuturor condensatoarelor sunt aceleași (C 2 \u003d C 3 și C 5 \u003d C 6), ambele ramuri paralele sunt simetrice, prin urmare potențialele punctelor A și B, situate egal în ramuri, trebuie să fie egale. Condensatorul C4 este astfel conectat la puncte cu diferență de potențial zero. Prin urmare, condensatorul C4 nu este încărcat, adică. poate fi exclusă iar schema prezentată în starea problemei poate fi simplificată (fig. b).
Soluţie
.
Dacă deconectați condensatorul C 4 de la circuit, obțineți o conexiune a condensatoarelor, care este ușor de calculat. Deoarece capacitățile tuturor condensatoarelor sunt aceleași (C 2 \u003d C 3 și C 5 \u003d C 6), ambele ramuri paralele sunt simetrice, prin urmare potențialele punctelor A și B, situate egal în ramuri, trebuie să fie egale. Condensatorul C4 este astfel conectat la puncte cu diferență de potențial zero. Prin urmare, condensatorul C4 nu este încărcat, adică. poate fi exclusă iar schema prezentată în starea problemei poate fi simplificată (fig. b).
Acest circuit este format din trei ramuri paralele, dintre care două conțin doi condensatori în serie.
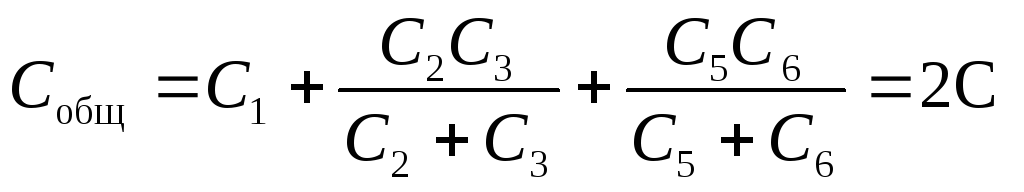
Răspuns: C total = 2C.
Exemplul 12.7. Condensator de aer plat cu capacitate C 1 \u003d 4pF încărcat la o diferență de potențialU 1 =100V. După deconectarea condensatorului de la sursa de tensiune, distanța dintre plăcile condensatorului a fost dublată. Determinați: 1) diferența de potențialU 2 pe plăcile condensatorului după separarea lor; 2) munca forțelor externe pentru a împinge plăcile în afară.
Dat: C 1 \u003d 4pF \u003d 4 ∙ 10 -12 F; U 1 \u003d 100V; d 2 \u003d 2d 1.
Găsi: 1) U2;2)A.
Soluţie . Încărcarea plăcilor condensatorului după deconectarea de la sursa de tensiune nu se modifică, adică. Q=const. De aceea
C 1 U 1 \u003d C 2 U 2, (1)
unde C 2 și U 2 sunt, respectiv, capacitatea și diferența de potențial de pe plăcile condensatorului după ce acestea sunt îndepărtate.
Având în vedere că capacitatea unui condensator plat 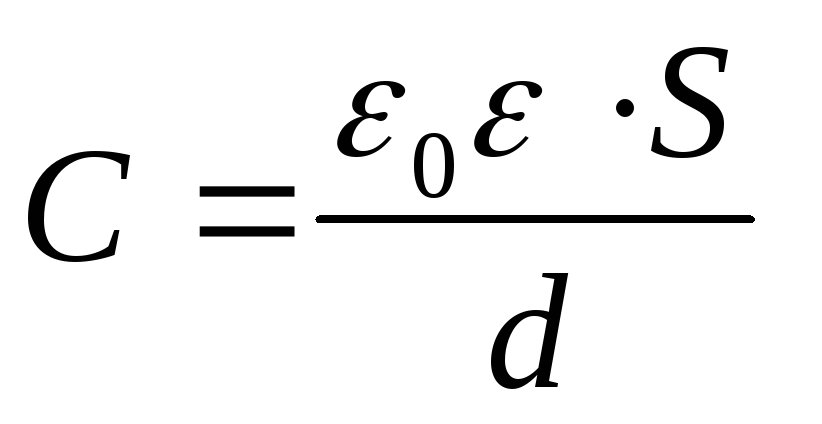 , din formula (1) obținem diferența de potențial dorită
, din formula (1) obținem diferența de potențial dorită
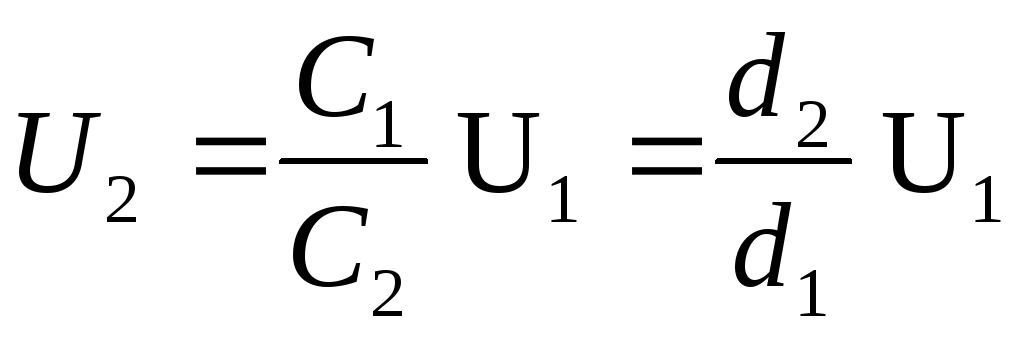 (2)
(2)
După deconectarea condensatorului de la sursa de tensiune, sistemul a două plăci încărcate poate fi considerat închis, pentru care este îndeplinită legea conservării energiei: lucrul A al forțelor externe este egal cu modificarea energiei sistemului.
A \u003d W 2 - W 1 (3)
unde W 1 și W 2 sunt energia câmpului condensatorului în starea inițială și, respectiv, finală.
Dat fiind 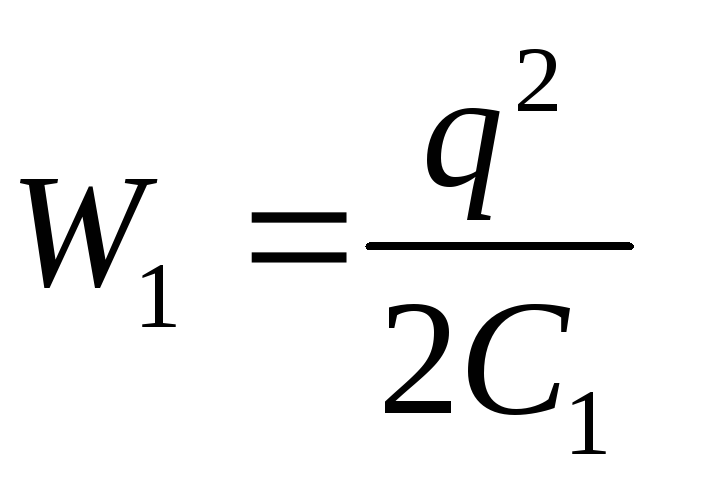 și
și 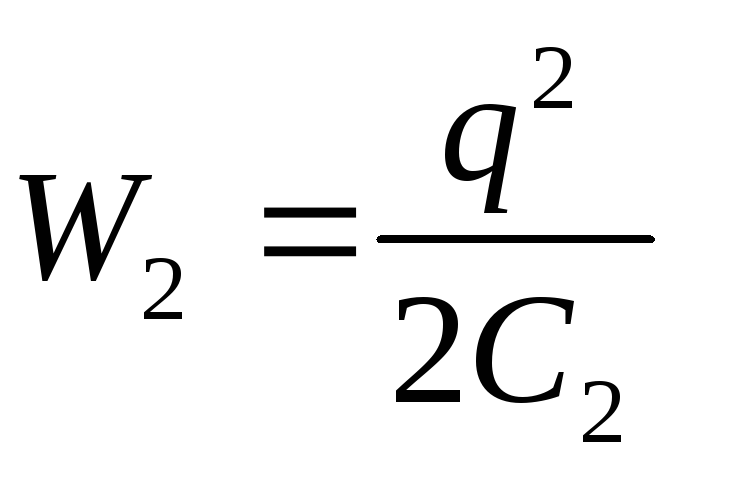 (q – const), din formula (3) se obține munca dorită a forțelor exterioare
(q – const), din formula (3) se obține munca dorită a forțelor exterioare
[ținând cont de faptul că q=C 1 U 1 și formula (2)].
Răspuns : 1) U 2 \u003d 200V; 2) A \u003d 40nJ.
Exemplul 12.7. O bilă solidă de dielectric cu o razăR=5cm încărcat uniform cu densitatea în vrac ρ=5nC/m 3 . Determinați energia câmpului electrostatic conținut în spațiul din jurul mingii.
Dat: R=5cm=5∙10 -2 m; ρ=5nC/m 3 = 5∙10 -9 C/m 3.
Găsi: W.
Soluţie . Câmpul unei bile încărcate este simetric sferic, astfel încât densitatea de sarcină volumetrică este aceeași în toate punctele situate la distanțe egale de centrul bilei.
E 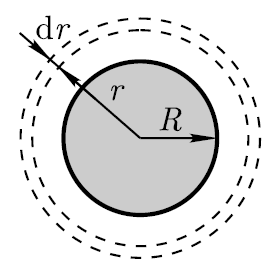 energie într-un strat sferic elementar (este ales în afara dielectricului, unde ar trebui determinată energia) cu un volum de dV (vezi figura)
energie într-un strat sferic elementar (este ales în afara dielectricului, unde ar trebui determinată energia) cu un volum de dV (vezi figura)
unde dV=4πr 2 dr (r este raza unui strat sferic elementar; dr este grosimea acestuia); 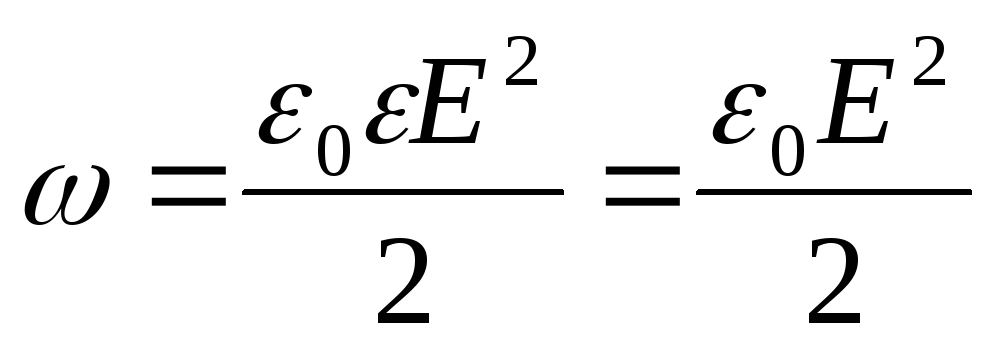 (ε=1 – câmp în vid; E – intensitatea câmpului electrostatic).
(ε=1 – câmp în vid; E – intensitatea câmpului electrostatic).
Vom găsi intensitatea E după teorema lui Gauss pentru un câmp în vid, iar ca suprafață închisă alegem mental o sferă cu raza r (vezi figura). În acest caz, întreaga încărcătură a mingii, care creează câmpul luat în considerare, ajunge în interiorul suprafeței și, conform teoremei lui Gauss,
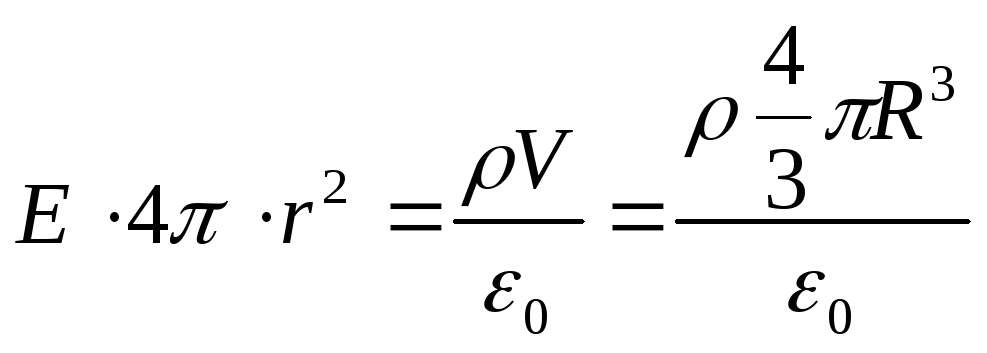
Unde 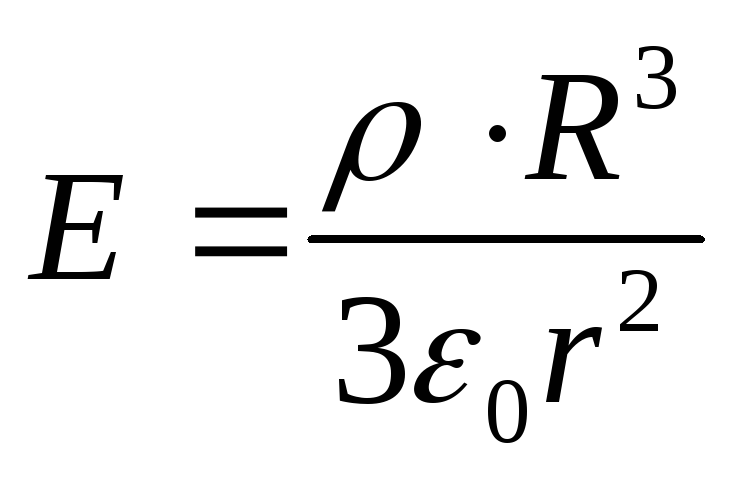
Înlocuind expresiile găsite în formula (1), obținem
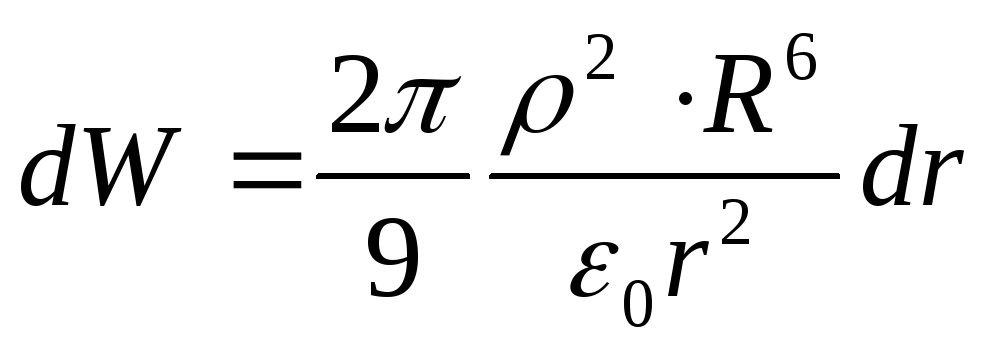
Energia conținută în spațiul din jurul mingii,
Răspuns: W=6,16∙10-13 J.
Exemplul 12.7. Condensator plan cu zona plăcilorSiar distanța dintre ele ℓ se raportează încărcareaq, după care condensatorul este deconectat de la sursa de tensiune. Determinați forța de atracțieFîntre plăcile condensatorului, dacă constanta dielectrică a mediului dintre plăci este egală cu ε.
Dat : S; ℓ; q; ε .
Găsi: F.
Soluţie . Încărcarea plăcilor condensatorului după deconectarea de la sursa de tensiune nu se modifică, adică. q=const. Să presupunem că sub acțiunea forței de atracție F, distanța dintre plăcile condensatorului s-a modificat cu d ℓ . Atunci forța F funcționează
Conform legii conservării energiei, această muncă este egală cu pierderea de energie a condensatorului, adică.
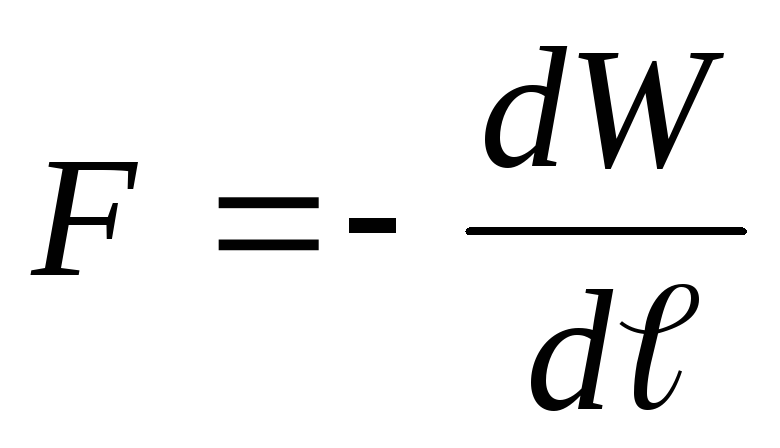 .
(3)
.
(3)
Înlocuind în formula energia unui condensator încărcat 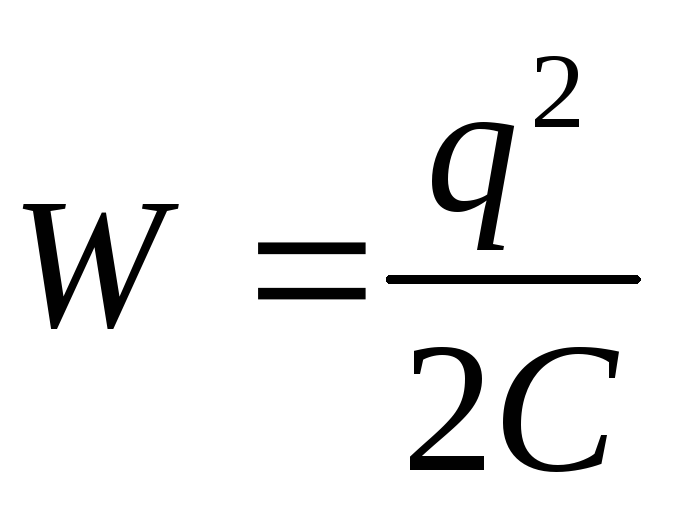 expresie pentru capacitatea unui condensator plat
expresie pentru capacitatea unui condensator plat 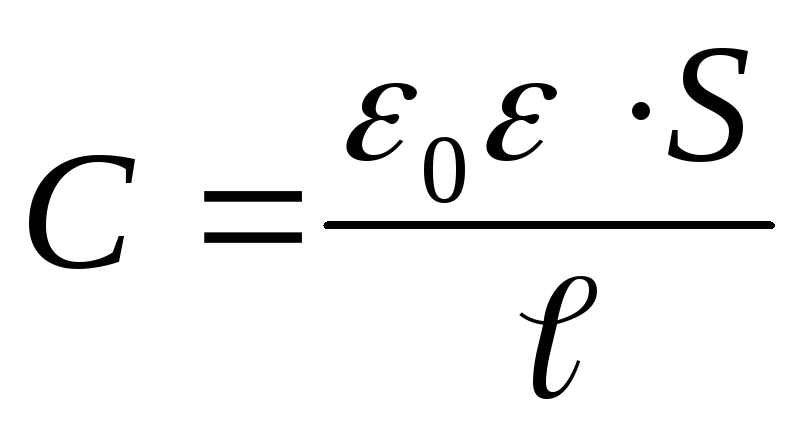 , primim
, primim
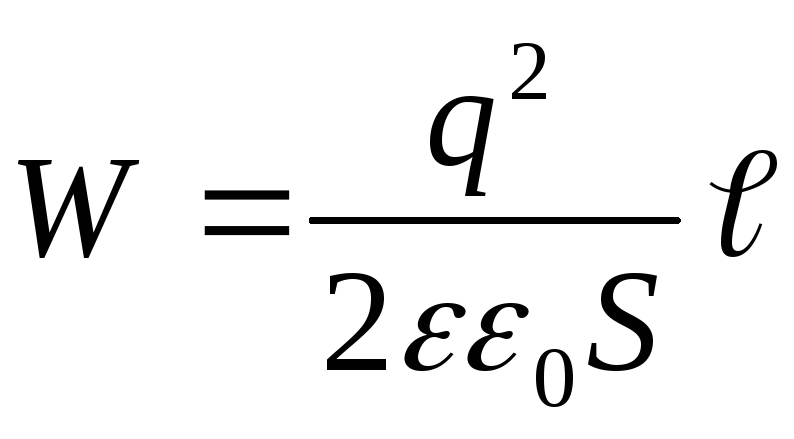 (4)
(4)
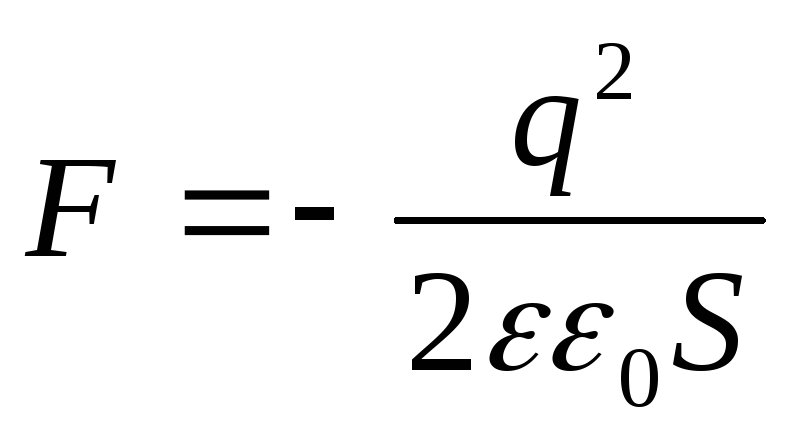
Răspuns:
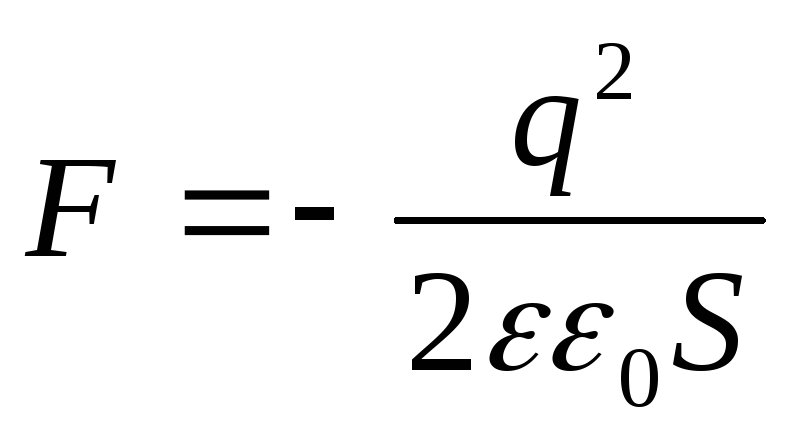
Exemplul 12.7. Condensator platSiar distanța dintre ele ℓ conectate la o sursă de tensiune constantăU. Determinați forța de atracțieFîntre plăcile condensatorului, dacă constanta dielectrică a mediului dintre plăci este egală cu ε.
Dat : S; ℓ; U; ε .
Găsi: F.
Soluţie . În funcție de starea problemei, pe plăcile condensatorului se menține o tensiune constantă, adică. U=const. Să presupunem că sub acțiunea forței de atracție F, distanța dintre plăcile condensatorului s-a modificat cu dℓ. Atunci forța F funcționează
Conform legii conservării energiei, această lucrare în acest caz duce la creșterea energiei condensatorului (comparați cu sarcina anterioară), adică.
de unde, pe baza expresiilor (1) și (2), obținem
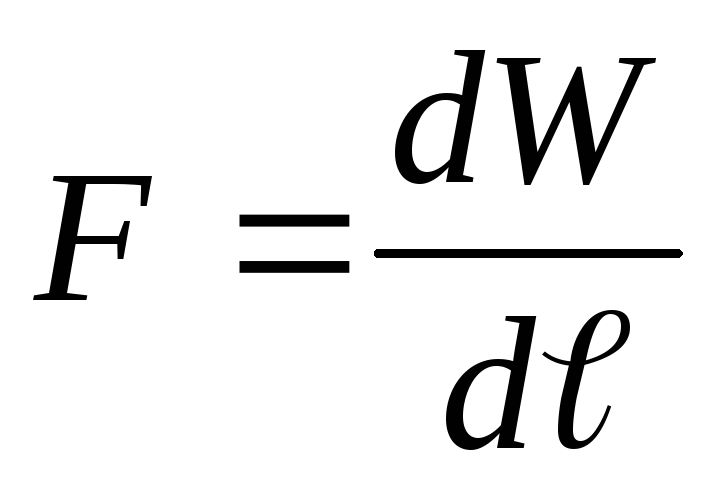 (3)
(3)
Înlocuind în formula energia condensatorului 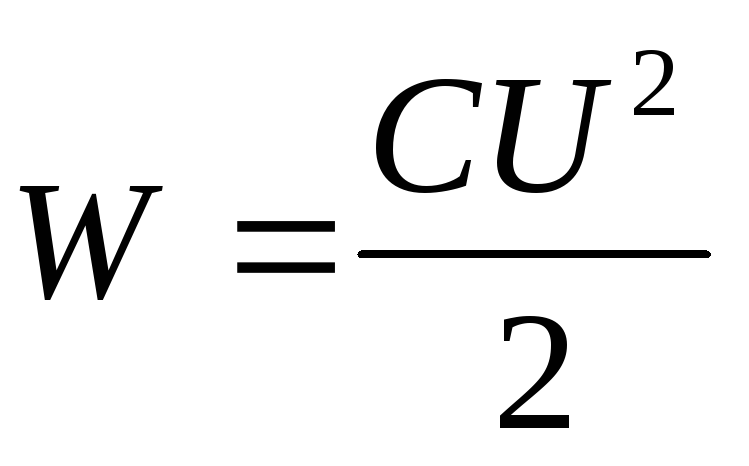 expresie pentru capacitatea unui condensator plat
expresie pentru capacitatea unui condensator plat  , primim
, primim
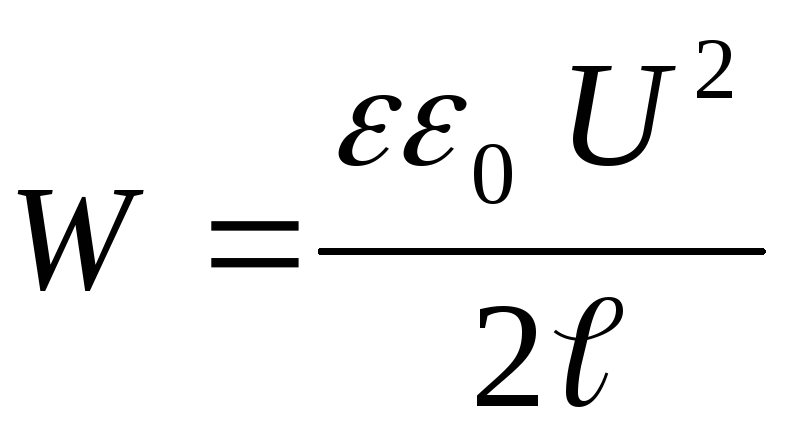 (4)
(4)
Înlocuind valoarea energetică (4) în formula (3) și efectuând diferențierea, găsim forța de atracție dorită între plăcile condensatorului.
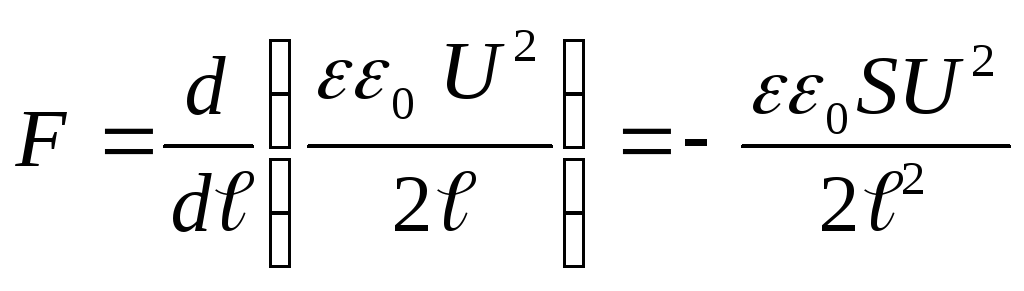 .
.
unde semnul „-” indică faptul că forța F este o forță de atracție.
Răspuns
: