Modelos descritos por sistemas de dos autónomos. ecuaciones diferenciales.

plano de fase. Retrato de fase. método de isoclina. isoclinas principales. Estabilidad en estado estacionario. Sistemas lineales. Tipos de puntos clave: nodo, silla, foco, centro. Ejemplo: reacciones químicas primer orden.

Los resultados más interesantes sobre la modelización cualitativa de las propiedades de sistemas biológicos se obtuvieron sobre modelos de dos ecuaciones diferenciales, que permiten un estudio cualitativo mediante el método plano de fase. Considere un sistema de dos ecuaciones diferenciales ordinarias autónomas de la forma general

(4.1)

P(x,y), Q(x,y)- funciones continuas definidas en algún dominio GRAMO Plano euclidiano ( x, y- Coordenadas cartesianas) y que tengan en esta zona derivadas continuas de orden no inferior a la primera.

Región GRAMO puede ser ilimitado o limitado. si variables x,y tienen un significado biológico específico (concentraciones de sustancias, abundancia de especies), la mayoría de las veces el área GRAMO es el cuadrante positivo del semiplano derecho:

0 £ X< ¥ ,0 £ y< ¥ .

Las concentraciones de sustancias o la abundancia de especies también pueden limitarse desde arriba por el volumen del recipiente o por la superficie del hábitat. Entonces el rango de variables tiene la forma:

0 £ X< x 0 , 0 £ y< y 0 .

variables x,y cambio en el tiempo de acuerdo con el sistema de ecuaciones (4.1), de modo que cada estado del sistema corresponde a un par de valores de variables ( x,y).

Por el contrario, para cada par de variables ( x,y) corresponde a un determinado estado del sistema.

Considere un plano con ejes de coordenadas en el que se trazan los valores de las variables. x, y. cada punto METRO este plano corresponde a un determinado estado del sistema. Este plano se llama plano de fase y representa la totalidad de todos los estados del sistema. El punto M(x, y) se llama punto de representación o representación.

Dejar en el momento inicial del tiempo. t=t 0 representa las coordenadas del punto METRO 0 (X(t 0), y(t 0)). En cada momento siguiente en el tiempo t el punto de representación se moverá según los cambios en los valores de las variables X(t), y(t). Cambio de agujas METRO(X(t), y(t)) en el plano de fase, cuya posición corresponde a los estados del sistema en el proceso de cambio de variables a lo largo del tiempo x(t), y(t) según las ecuaciones (4.1), se llama trayectoria de fase.

El conjunto de trayectorias de fase para diferentes valores iniciales de las variables proporciona un "retrato" fácilmente visible del sistema. Edificio retrato de fase le permite sacar conclusiones sobre la naturaleza de los cambios en las variables x,y sin conocer las soluciones analíticas del sistema de ecuaciones original(4.1).

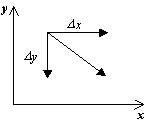
Para representar un retrato de fase, es necesario construir un campo vectorial de direcciones para las trayectorias del sistema en cada punto del plano de fase. Al especificar un incrementoD t>0,obtenemos los incrementos correspondientes D X Y D y de expresiones:

D x=P(x,y)D t,

D y=Q(x,y)D t.

dirección vectorial dy/dx en el punto ( x,y) depende del signo de las funciones P(x, y), Q(x, y) y puede ser dado por una tabla:

P(x,y)>0,Q(x,y)>0
P(x,y)<0,Q(x,y)<0
P(x,y)>0,Q(x,y)<0
P(x,y)<0,Q(x,y)>0

.(4.2)

Solución a esta ecuación y=y(x,c), o implícitamente F(x, y)=c, Dónde Con es la constante de integración, da la familia de curvas integrales de la ecuación (4.2) - trayectorias de fase sistema (4.1) en el avión x,y.

método de isoclina

Para construir un retrato de fase, se utiliza método de isoclina - Se dibujan líneas en el plano de fase que intersecan las curvas integrales en un ángulo específico. La ecuación de isoclina es fácil de obtener a partir de (4.2). Pongamos

Dónde A– una determinada constante. Significado A representa la tangente de la pendiente de la tangente a la trayectoria de fase y puede tomar valores de -¥ a + ¥ . Sustituyendo en lugar de dy/dx en (4.2) la cantidad A obtenemos la ecuación de isoclina:

.(4.3)

La ecuación (4.3) determina en cada punto del plano la única tangente a la curva integral correspondiente, excepto el punto donde P(x,y)= 0, Q (x, y) = 0 , en el que la dirección de la tangente se vuelve indefinida, ya que el valor de la derivada se vuelve indefinido:

.

Este punto es el punto de intersección de todas las isoclinas. punto especial. Simultáneamente desaparece las derivadas temporales de las variables. X Y y.

Por tanto, en el punto singular, las tasas de cambio de las variables son iguales a cero. Por tanto, el punto singular de las ecuaciones diferenciales de trayectorias de fase (4.2) corresponde a estado estacionario del sistema(4.1), y sus coordenadas son los valores estacionarios de las variables x, y.

De particular interés son principales isoclinas:

dy/dx=0, P(x, y)=0 – isoclina de tangentes horizontales y

dy/dx=¥ , q(x, y)=0 – isoclina de tangentes verticales.

Construyendo las isoclinas principales y encontrando el punto de su intersección. (x,y), cuyas coordenadas cumplen las condiciones:

Así encontraremos el punto de intersección de todas las isoclinas del plano de fase, en el que la dirección de las tangentes a las trayectorias de fase es indefinida. Este - punto singular, que corresponde estado estacionario del sistema(Figura 4.2).

El sistema (4.1) tiene tantos estados estacionarios como puntos de intersección de las isoclinas principales en el plano de fase.

Cada trayectoria de fase corresponde a un conjunto de movimientos de un sistema dinámico que pasan por los mismos estados y se diferencian entre sí sólo por el comienzo de la referencia temporal.

Si se cumplen las condiciones del teorema de Cauchy, entonces a través de cada punto del espacio x, y, t pasa por una sola curva integral. Lo mismo ocurre, gracias a la autonomía, con las trayectorias de fase: una trayectoria de fase única pasa por cada punto del plano de fase.

Estabilidad en estado estacionario

Dejemos que el sistema esté en equilibrio.

Entonces el punto representativo se ubica en uno de los puntos singulares del sistema, en el cual, por definición:

.

Si un punto singular es estable o no está determinado por si el punto representativo sale o no con una pequeña desviación del estado estacionario. Aplicada a un sistema de dos ecuaciones, la definición de estabilidad en el lenguajemi, dcomo sigue.

El estado de equilibrio es estable si para cualquier área dada de desviaciones del estado de equilibrio (mi )El área se puede especificar. d (mi ), rodeando el estado de equilibrio y teniendo la propiedad de que ninguna trayectoria que comience dentro de la región d , nunca llegará a la frontera mi . (Figura 4.4)

Para una gran clase de sistemas: sistemas rugosos – cuya naturaleza de comportamiento no cambia con un pequeño cambio en el tipo de ecuaciones, se puede obtener información sobre el tipo de comportamiento en las proximidades del estado estacionario estudiando no el original, sino el simplificado. linealizado sistema.

Sistemas lineales.

Considere un sistema de dos ecuaciones lineales:

.(4.4)

Aquí a B C D- constantes, x,y- Coordenadas cartesianas en el plano de fase.

La solución general se buscará en la forma:

.(4.5)

Sustituya estas expresiones en (4.4) y reduzca por mi yo t:

(4.6)

Sistema algebraico de ecuaciones (4.6) con incógnitas A, B tiene solución distinta de cero sólo si su determinante, compuesto por los coeficientes de las incógnitas, es igual a cero:

.

Ampliando este determinante, obtenemos la ecuación característica del sistema:

.(4.7)

La solución de esta ecuación da los valores del indicador.yo 1,2 , bajo el cual son posibles valores distintos de cero para A Y B soluciones de la ecuación (4.6). Estos valores son

.(4.8)

Si la expresión radical es negativa, entoncesyo 1,2 números conjugados complejos. Supongamos que ambas raíces de la ecuación (4.7) tienen partes reales distintas de cero y que no hay raíces múltiples. Entonces la solución general del sistema (4.4) se puede representar como una combinación lineal de exponentes con exponentesyo 1 , yo 2 :

(4.9)

Para analizar la naturaleza de las posibles trayectorias del sistema en el plano de fase, utilizamos transformación de coordenadas lineal homogénea, que llevará el sistema a forma canónica:

,(4.10)

lo que permite una representación más conveniente en el plano de fase en comparación con el sistema original (4.4). Introduzcamos nuevas coordenadas.ξ , η según las fórmulas:

(4.1)

Se sabe por el curso de álgebra lineal que si las partes reales no son iguales a ceroyo 1 , yo 2 el sistema original (4.4) con la ayuda de transformaciones (4.11) siempre se puede transformar a la forma canónica (4.10) y se puede estudiar su comportamiento en el plano de fases.ξ , η . Consideremos los diversos casos que pueden presentarse aquí.

Raíces λ 1 , λ 2 – válido y del mismo signo

En este caso los coeficientes de transformación son reales, nos movemos del plano real.x,yal plano real ξ, η. Dividiendo la segunda de las ecuaciones (4.10) por la primera, obtenemos:

.(4.12)

Integrando esta ecuación encontramos:

Donde .(4.13)

Acordemos entender por λ 2 la raíz de la ecuación característica con un módulo grande, que no viola la generalidad de nuestro razonamiento. Entonces, dado que en el caso considerado las raíces λ 1 , λ2 – válido y del mismo signo,a>1 , y estamos ante curvas integrales de tipo parabólica.

Todas las curvas integrales (excepto el eje η , que corresponde a ) toque en el origen del eje ξ, que también es una curva integral de la ecuación (4.11). El origen de coordenadas es un punto singular.

Averigüemos ahora la dirección del movimiento del punto representativo a lo largo de las trayectorias de fase. Si λ 1 , λ 2 son negativos, entonces, como se puede ver en las ecuaciones (4.10), |ξ|, |η| disminuir con el tiempo. El punto de representación se acerca al origen, pero nunca llega a él. De lo contrario, esto contradeciría el teorema de Cauchy, que establece que sólo una trayectoria de fase pasa por cada punto del plano de fase.

Un punto tan singular por el que pasan curvas integrales, como una familia de parábolas pasa por el origen de coordenadas, se llama nodo (Fig. 4.5)

Estado de equilibrio tipo nudo en λ 1 , λ 2 < 0 es estable según Lyapunov, ya que el punto de representación se mueve a lo largo de todas las curvas integrales hacia el origen de coordenadas. Este nudo estable. Si λ 1 , λ 2 > 0, entonces |ξ|, |η| aumenta con el tiempo y el punto representativo se aleja del origen. En este caso, el punto singular– nodo inestable .

En el plano de fase x,y Se mantendrá el carácter cualitativo general del comportamiento de las curvas integrales, pero las tangentes a las curvas integrales no coincidirán con los ejes de coordenadas. El ángulo de inclinación de estas tangentes vendrá determinado por la relación de los coeficientes α , β , γ , δ en las ecuaciones (4.11).

Raíces λ 1 , λ 2 son válidos y tienen signos diferentes.

Convertir de coordenadas x, y a coordenadas ξ, η otra vez real. Las ecuaciones para las variables canónicas nuevamente tienen la forma (4.10), pero ahora los signos λ 1 , λ 2 diferente. La ecuación de la trayectoria de fase tiene la forma:

Donde, (4.14)

Integrando (4.14), encontramos

(4.15)

Este La ecuación define una familia de curvas de tipo hiperbólico, donde ambos ejes coordenados son las asíntotas (en a=1 tendríamos una familia de hipérbolas isósceles). Los ejes de coordenadas también son curvas integrales en este caso.– estas serán las únicas curvas integrales que pasan por el origen. Cadade los cuales consta de trayectorias de tres fases: de dos movimientos hacia un estado de equilibrio (o alejamiento de un estado de equilibrio) y desde un estado de equilibrio. Todas las demás curvas integrales– Son hipérbolas que no pasan por el origen (Fig. 4.6) Este punto singular se llama "sillín ». Las líneas de nivel cerca de la montaña se comportan como trayectorias de fase en las proximidades de la montaña.

Consideremos la naturaleza del movimiento del punto representativo a lo largo de trayectorias de fase cercanas al estado de equilibrio. Dejemos, por ejemplo,λ 1 > 0 , λ 2<0 . Entonces el punto representativo colocado sobre el eje ξ , se alejará del origen y se colocará en el eje η – se acercará indefinidamente al origen de coordenadas, sin alcanzarlo en tiempo finito. Dondequiera que esté el punto representativo en el momento inicial (con excepción del punto singular y los puntos en la asíntota η =0), eventualmente se alejará del estado de equilibrio, incluso si al principio se mueve a lo largo de una de las curvas integrales hacia un punto singular.

Es obvio que El punto singular tipo silla de montar siempre es inestable. . Sólo bajo condiciones iniciales especialmente elegidas en la asíntotaη =0 el sistema se acercará a un estado de equilibrio. Sin embargo, esto no contradice la afirmación de que el sistema es inestable. si cuentas, que todos los estados iniciales del sistema en el plano de fase son igualmente probables, entonces la probabilidad de tal estado inicial que corresponda al movimiento en la dirección A el punto singular es igual a cero. Por tanto, cualquier movimiento real sacará al sistema del estado de equilibrio.Volviendo a las coordenadasx, y,obtenemos la misma imagen cualitativa de la naturaleza del movimiento de trayectorias alrededor del origen.

El límite entre los casos considerados de un nodo y una silla de montar es el caso Cuando uno de los indicadores característicos, por ejemplo λ 1 , desaparece, lo que ocurre cuando el determinante del sistema- expresión adbc=0(ver fórmula 4.8 ). En este caso, los coeficientes de los lados derechos de las ecuaciones (4.4) son proporcionales entre sí.:

y el sistema tiene por estados de equilibrio todos los puntos de la recta:

Las curvas integrales restantes son una familia de rectas paralelas con pendiente , a lo largo del cual los puntos representativos se acercan al estado de equilibrio o se alejan de él, dependiendo del signo de la segunda raíz de la ecuación característica λ 2 = a+d.(Figura 4.7 ) En este caso, las coordenadas del estado de equilibrio dependen del valor inicial de las variables.

Raíces λ 1 , λ 2 – complejoconjugado

En este caso, de verdad.X Y y Lo haremos tener conjugados complejos ξ , η (4.10) . Sin embargo, introduciendo una transformación intermedia más, también es posible en este caso reducir la consideración a una transformación lineal homogénea real. Pongamos:

(4.16)

Dónde a, b, Y u,v – valores reales. Se puede demostrar que la transformación dex,y A tú, v es, según nuestros supuestos, real, lineal, homogéneo con un determinante distinto de cero. Debido a las ecuaciones(4.10, 4.16) tenemos:

dónde

(4.17)

Dividiendo la segunda de las ecuaciones por la primera, obtenemos:

que es más fácil de integrar, si cambiamos al sistema de coordenadas polares (r, φ ) . Después de la sustitución obtenemos de donde:

.(4.18)

Así, en el plano de fasetú, vEstamos tratando con una familia de espirales logarítmicas, cada una de las cuales tienePunto asintótico en el origen.Punto singular que es el punto asintótico de todas las curvas integrales que tienen forma de espirales., amigo anidado enamigo, llamado enfocar ( figura 4.8 ) .

Consideremos la naturaleza del movimiento del punto representativo a lo largo de las trayectorias de fase. Multiplicando la primera de las ecuaciones (4.17) portu, y el segundo a v y sumando obtenemos:

Dónde

Dejar a 1 < 0 (a 1 = Reλ ) . El punto de representación se acerca entonces continuamente al origen, sin llegar a él en un tiempo finito. Esto significa que las trayectorias de fase son espirales torcidas y corresponden a oscilaciones amortiguadas. variables. Este - enfoque constante .

En el caso de un foco estable, como en el caso de un nodo estable, no solo se cumple la condición de Lyapunov, sino también un requisito más estricto. Es decir, ante cualquier desviación inicial, el sistema eventualmente regresará tan cerca como se desee de la posición de equilibrio. Tal estabilidad, en la que las desviaciones iniciales no solo no aumentan, sino que decaen, tendiendo a cero, se llama estabilidad absoluta .

Si en la fórmula (4.18) a 1 >0 , entonces el punto representativo se aleja del origen y estamos ante enfoque inestable . Al pasar de un aviónu,val plano de faseX, yLas espirales también seguirán siendo espirales, pero se deformarán.

Consideremos ahora el caso cuandoa 1 =0 . Trayectorias de fase en el avión.tú, vhabrá círculos cual en el avionx,yajustar elipses:

Así, enun 1=0 a través de un punto especialx= 0,y= 0 no pasa ninguna curva integral. Un punto singular aislado, cerca del cual las curvas integrales son curvas cerradas, en particular, elipses incrustadas entre sí y que encierran el punto singular, se llama centro.

Por tanto, son posibles seis tipos de equilibrio, dependiendo de la naturaleza de las raíces de la ecuación característica (4.7). Vista de trayectorias de fase en el avión. x,y Para estos seis casos se muestra en la Fig. 4.9.

Arroz. 4.9.Tipos de retratos de fase en las proximidades de un estado estacionario para el sistema de ecuaciones lineales (4.4).

Los cinco tipos de estados de equilibrio son aproximados; su naturaleza no cambia con cambios suficientemente pequeños en los lados derechos de las ecuaciones (4.4). En este caso, los cambios deberían ser pequeños no sólo en los lados derechos, sino también en sus derivadas de primer orden. El sexto estado de equilibrio, el centro, no es tosco. Con pequeños cambios en los parámetros del lado derecho de las ecuaciones, entra en un foco estable o inestable.

Diagrama de bifurcación

Introduzcamos la notación:

. (4.11)

Entonces la ecuación característica se puede escribir en la forma:

. (4.12)

Considere un plano con coordenadas cartesianas rectangulares. s , D y marque en él las áreas correspondientes a uno u otro tipo de estado de equilibrio, que está determinado por la naturaleza de las raíces de la ecuación característica.

.(4.13)

La condición para la estabilidad del estado de equilibrio será la presencia de una parte real negativa de yyo 1 y yo 2 . Una condición necesaria y suficiente para ello es el cumplimiento de las desigualdades.s > 0, D > 0 . En el diagrama (4.15), esta condición corresponde a los puntos ubicados en el primer cuarto del plano de parámetros. El punto singular será el foco siyo 1 y yo 2 complejo. Esta condición corresponde a aquellos puntos del plano para los cuales , aquellos. puntos entre dos ramas de una parábolas 2 = 4 D. Puntos del semieje s = 0, D>0, corresponden a estados de equilibrio del tipo centro. Asimismo,yo 1 y yo 2 - signos válidos, pero diferentes, es decir un punto singular será una silla de montar si D<0, etc. Como resultado, obtenemos un diagrama de partición del plano de parámetros. s, D, en regiones correspondientes a diferentes tipos de estados de equilibrio.

Arroz. 4.10. Diagrama de bifurcación

para el sistema de ecuaciones lineales 4.4

Si los coeficientes del sistema lineal a B C D dependen de algún parámetro, entonces cuando se cambia este parámetro, los valores también cambiaráns , D . Al atravesar los límites, la naturaleza del retrato de fase cambia cualitativamente. Por lo tanto, tales límites se denominan límites de bifurcación: en lados opuestos del límite, el sistema tiene dos retratos de fase topológicamente diferentes y, en consecuencia, dos tipos diferentes de comportamiento.

El diagrama muestra cómo pueden ocurrir tales cambios. Si excluimos casos especiales (el origen de las coordenadas), entonces es fácil ver que la silla puede entrar en un nodo, estable o inestable, al cruzar el eje y. Un nodo estable puede moverse a una silla o a un foco estable, y así sucesivamente. Tenga en cuenta que las transiciones nodo estable-enfoque estable y nodo inestable-enfoque inestable no son bifurcacionales, ya que la topología del espacio de fase no cambia en este caso. Hablaremos con más detalle sobre la topología del espacio de fase y las transiciones de bifurcación en la Clase 6.

En las transiciones de bifurcación, la naturaleza de la estabilidad del punto singular cambia. Por ejemplo, un foco estable a través del centro puede convertirse en un foco inestable. Esta bifurcación se llama Bifurcación de Andronov-Hopf por los nombres de los científicos que lo estudiaron. Con esta bifurcación en sistemas no lineales, nace un ciclo límite y el sistema se vuelve autooscilante (ver lección 8).

Ejemplo. Sistema de reacciones químicas lineales.

Sustancia X Fluye desde el exterior a una velocidad constante, se convierte en la sustancia Y y a una velocidad proporcional a la concentración de la sustancia. Y, se saca de la esfera de reacción. Todas las reacciones son de primer orden, a excepción de la entrada de materia del exterior, que es de orden cero. El esquema de reacción es el siguiente:

(4.14)

y se describe mediante el sistema de ecuaciones:

(4.15)

Obtenemos concentraciones estacionarias igualando los lados derechos a cero:

.(4.16)

Considere el retrato de fases del sistema. Dividamos la segunda ecuación del sistema (4.16) por la primera. Obtenemos:

.(4.17)

La ecuación (4.17) determina el comportamiento de las variables en el plano de fase. Construyamos un retrato de fase de este sistema. Primero, dibujamos las isoclinas principales en el plano de fase. Ecuación de la isoclina de tangentes verticales:

Ecuación para la isoclina de tangentes horizontales:

El punto singular (estado estacionario) se encuentra en la intersección de las isoclinas principales.

Ahora determinemos en qué ángulo los ejes de coordenadas se cruzan con las curvas integrales.

Si x= 0, entonces.

Por tanto, la tangente de la pendiente de la tangente a las curvas integrales. y=y(x), cruzando el eje y x=0, es negativo en el semiplano superior (recordemos que las variables x,y tienen valores de concentración, y por lo tanto sólo nos interesa el cuadrante superior derecho del plano de fase). En este caso, el valor de la tangente del ángulo de inclinación de la tangente aumenta con la distancia al origen.

Considere el eje y= 0. En la intersección de este eje, las curvas integrales están descritas por la ecuación

En la tangente de la pendiente de las curvas integrales que cruzan el eje de abscisas es positiva y aumenta de cero a infinito al aumentar X.

En .

Luego, con un aumento adicional, la tangente de la pendiente disminuye en valor absoluto, quedando negativa y tiende a -1 en X ® ¥ . Conociendo la dirección de las tangentes a las curvas integrales en las isoclinas principales y en los ejes de coordenadas, es fácil construir la imagen completa de las trayectorias de fase.

La naturaleza de la estabilidad del punto singular se establecerá mediante el método de Lyapunov. El determinante característico del sistema tiene la forma:

.

Ampliando el determinante, obtenemos la ecuación característica del sistema: , es decir. las raíces de la ecuación característica son ambas negativas. Por tanto, el estado estacionario del sistema es un nodo estable. Al mismo tiempo, la concentración de la sustancia. X tiende a un estado estacionario siempre de forma monótona, la concentración de la sustancia Y puede pasar por min o max. Los regímenes oscilatorios en un sistema así son imposibles.

Dejar zq - punto singular de la función f(z), t.s. f(z) pero es analítico en este punto (en particular, puede que no esté definido en él). Si existe una vecindad tan perforada del punto zq (es decir, el conjunto O z - zq f(z) es aliatico, entonces zo llamado punto singular aislado funciones f(z). Esta definición también se conserva en el caso zn = oo, si el yodo es una vecindad perforada de un punto zq = oo entender el conjunto z > I - la aparición de algún círculo centrado en el origen. En otras palabras, el punto singular Se dice que zq está aislado si existe una vecindad de este punto en la que existen otros puntos singulares diferentes de zq. A continuación, consideramos sólo puntos singulares de un carácter de un solo valor (la función f(z) se supone que es único).

Dependiendo del comportamiento de la función. f(z) en z -> zq Hay tres tipos de puntos singulares. Punto singular aislado funciones zq f(z) llamado:

1) punto singular removible si hay un límite finito

2) polo si hay un limite

3) punto esencial, Si f(z)) no tiene límite finito ni infinito para z-> zq.

EJEMPLO 26.1. Demostremos que se realizan los tres tipos de puntos singulares. Considerar F(z)= punto zq = 0 está aislado

punto singular de esta función. Usando la fórmula (22.12), obtenemos la expansión

de lo cual se deduce que existe lim fi(z)= 1. Por lo tanto, zq = 0 es

es un punto singular removible de la función fi(z).

Función f'j(z) =--- tiene un polo en un punto zo= 1 porque

2 r" X

Consideremos ahora la función )z(z)= e 1 ^ r y demuestre que zo = O es un punto singular esencial de esta función. Al esforzarse z a cero a lo largo del eje real, los límites izquierdo y derecho de la función f (z) diferente: lim Con 1 / 1 = 0,lím con 1 /* = os. Esto implica,

x->0-0 x->0+0

Qué f:i(z) no tiene límite finito ni infinito para 2 -> Ah, es decir zq = 0 es un punto singular esencial de esta función. (Tenga en cuenta que a medida que el punto tiende z-iy a cero en la función del eje imaginario

no tiene ningún límite.)

Por supuesto, también existen puntos singulares no aislados. Por ejemplo. la función tiene polos en los puntos zn = -, PAG= ±1, ±2,...

Por eso, Zq = 0 es un punto singular no aislado de esta función: en cualquier vecindad (arbitrariamente pequeña) de este punto hay otros puntos singulares gp.

Dejar zo- punto singular aislado final de una función f(z). Entonces f(z) es similar en algún barrio pinchado 0 Zo del punto zo esta vecindad puede considerarse como un anillo con radio interior r = 0. Según el teorema 25.1, en la vecindad considerada, la función f(z) se puede ampliar en una serie de Laurent (25.2). Demostraremos que el comportamiento de la función para 2 -> zq (es decir, el tipo de punto singular zo) depende de la forma de la parte principal de la descomposición (25.2); esta circunstancia explica el origen del término “parte principal”.

TEOREMA 2G.2. Un punto singular aislado zo de una función f(z) es removible si y sólo si la expansión de Lorap en una vecindad perforada de este punto tiene la oid

aquellos. consta solo de la parte correcta, y todos los coeficientes de la parte principal son iguales a la viñeta.

Prueba. 1. dejar zo es un punto singular removible. Demostremos que la expansión de Laurent de la función f(z) tiene la forma (26.1). Desde el punto singular zo extraíble, entonces hay un límite finito lim f(z) = A. Por eso, f(z) delimitado en alguna vecindad perforada 0 z - zq del punto zo, aquellos. )(z) para todos z de este barrio. Tomar cualquiera r. U р /?|, y utilice las fórmulas (25.3) para los coeficientes de la serie de Laurent:

Para los coeficientes de la parte principal de la expansión. norte =- 1,-2,... Para tales valores PAG tenemos p~n-e 0 en R-> 0. Desde el valor R se puede elegir arbitrariamente pequeño, entonces Señor~" puede ser arbitrariamente pequeño. Desde |c t,| ^ Señor ~ n y cn no dependen de p, entonces cn = 0 para Y= - 1, -2,..., lo cual estaba por demostrar.

2. Supongamos ahora que el desarrollo de Laurent tiene la forma (26.1). La serie (26.1) es una serie de potencias y. por tanto, converge no sólo en los pinchados, sino también en todo el barrio z-zq incluyendo el punto zo; su suma S(z) es analítico para z y S(z) = )(z) a las 0 z - zo r. Por lo tanto, existe un límite finito lim )(z)\u003d Pm 5 (r) \u003d 5 (r) - Por lo tanto, el punto singular zq

Z->Zo Z-*Zo

desechable. El teorema ha sido demostrado.

Comentario. De la demostración del teorema se deduce que en una vecindad perforada 0 z - zo de un punto singular removible, la función f(z) coincide con la función S(r), que es analítica en toda la vecindad z - zo. Por tanto, si ponemos /(th) = S(zq), luego, sin cambiar los valores de la función. f(z) en cualquier punto de la vecindad perforada, hacemos que esta función sea analítica en r, es decir, “eliminar” la función. Esto explica el término "singularidad removible". Es natural considerar tales puntos como regulares y no como puntos singulares de la función. f(z).

Consideremos, por ejemplo, la función

En el ejemplo 26.1, se demostró que Pm (n) = 1, es decir punto singular

zq = 0 es extraíble. Si establecemos /i(0) = 1, eliminamos la singularidad y obtenemos una función que es analítica en el punto zq = 0 (y en todo el plano C).

Caractericemos ahora los polos en términos de expansiones de Laurent.

Teorema 26.3. Un punto singular aislado Zo de una función f(z) es un polo si y sólo si, cuando la parte principal del desarrollo de Laurent con centro Zq tiene sólo un número finito de elementos distintos

desde cero coeficientes con n:

Prueba. 1. dejar zq - polo, es decir lím /( z) = oo.

Demostremos que la expansión de Laurent de la función f(z) tiene la forma (2G.2). desde lim f(z)=oo. entonces existe una vecindad perforada del punto

ki zq. donde f(z) es analítico y no tiene ceros. Entonces la función gramo(z) = 1 /f(z) también será analítico en este vecindario perforado, y lim gramo(z)= 0. Por lo tanto, Zo es desechable *-? *0

punto singular de la función g(z). vamos a redefinir gramo(z) en el punto zo, poniendo g(zo)= 0. Entonces gramo(z) se vuelve analítico en toda la vecindad del punto (no perforado) z0, y z0 será su cero aislado. Denotamos por norte multiplicidad (orden) de este cero. Como se mostró en §23, en una vecindad del punto función zq gramo(z) representable en la forma (ver (23.2))

y (z$)f 0 y y>(z) es analítico en alguna vecindad del punto zo- Porque dirección IP(z) continuo en el punto zo Y g>(zo)F 0" entonces dirección IP(z) tampoco tiene ceros en alguna vecindad de este punto. Por lo tanto la función 1 /-p(z) también será analítico en esta vecindad y, por lo tanto, se expande en ella en una serie de Taylor:

Ampliando los paréntesis y cambiando las designaciones de los coeficientes, escribimos la última expansión en la forma

donde c_jv = 1>o f 0. Así, la parte principal del desarrollo de Laurent de f(r) contiene sólo un número finito de términos; hemos llegado a la igualdad requerida (26.2).

2. Dejar entrar una zona perforada de un punto. th función )(z) está representado por la expansión de Laurent (26.2) (en una forma más ampliada, ver (26.3)), la parte principal de la cual contiene sólo un número finito de términos, y Con- d" F 0. Debemos demostrar que Zq - polo de función f(z). Multiplicando la igualdad (26.3) por (GRAMO - GRAMO o) iV , obtenemos la función

La serie en (26.4) es una serie de potencias que converge a una función analítica no sólo en el punto perforado, sino también en toda la vecindad del punto Zq. Por lo tanto, la función h(z) se vuelve analítico en este vecindario si lo extendemos en th estableciendo h(zo)= s_dg F 0. Entonces

Por tanto, el punto o es un polo y se demuestra el teorema 26.3.

Multiplicidad (orden) de la función cero. gramo(z)= 1//(r) se llama orden de polos función /(r). Si NORTE- el orden del polo es th, entonces gramo(z)= (r - Zo)Nip(z), y ve) F 0 y, como se muestra en la primera parte de la demostración del Teorema 26.3, el desarrollo de f(r) tiene la forma (26.3), donde c_/v F 0. Por el contrario, si f(r) se expande en la serie (26.3) y ez F 0, entonces

t.s. NORTE- el orden del polo de la función f(r). De este modo, el orden del polo zq de la función/(GRAMO) es igual al número del coeficiente principal distinto de cero de la parte principal de la expansión de Laurent en la vecindad perforada del punto zq(es decir, igual a tal número NORTE, que s_dg F 0 y sp= 0 en PAG > NORTE).

Probemos la siguiente afirmación, que es conveniente) para aplicaciones.

Corolario 26.4. El punto zq es un polo de orden N de la ficción/(GRAMO) si y solo si/(GRAMO) representar en la forma

donde h(z) es una función analítica en la vecindad de un punto th y h(zo) f 0.

Prueba. Función cp(z) = l/h(z) es analítico en alguna vecindad del punto r. La condición del Corolario 26.4 es equivalente a lo siguiente:

Es por eso zq - multiplicidad cero norte funciones g(z). y de ahí el polo de multiplicidad norte funciones /(2).

II ejemplo 26.5. Encuentra puntos singulares aislados de una función. y determinar su tipo.

D e u c ció n. Los puntos en los que (z 2 + 1 )(z+ H) 2 = 0. Si z 2 L- 1 = 0 entonces 2 = ± g Si (z 4- H) 2 = 0, entonces z= -3. Por tanto, la función tiene tres puntos singulares. z= r, 22 = -r, z3 = - 3. Considere z:

GRAMO- polo de primer orden (usamos el Corolario 26.4). De manera similar se puede demostrar que 22 = -i también un polo de primer orden. Durante 2h tenemos:

Pasemos a la consideración de puntos esencialmente singulares.

Teorema 26.6. Un punto singular aislado zq de una función f(z) es esencialmente singular si y sólo si la parte principal de la expansión de Laurent centrada en zq tiene infinitas diferencias de. cero, coeficientes con p.

Prueba. El teorema 26.6 se deriva directamente de los teoremas 26.2 y 26.3. De hecho, si el punto zq es esencialmente singular, entonces la parte principal de la expansión de Laurent no puede estar ausente o contener un número finito de términos (de lo contrario, el punto Zq será removible o un poste). Por tanto, el número de términos de la parte principal debe ser infinito.

Por el contrario, si la parte principal contiene infinitos miembros, entonces Zq no puede ser ni un punto removible ni un polo. En consecuencia, este punto es esencialmente singular.

Según la definición, un punto esencialmente singular se caracteriza por el hecho de que la función f(2) no tiene límite finito ni infinito para z->zq. El siguiente teorema da una idea más completa de cuán irregular es el comportamiento de una función en la vecindad de un punto esencialmente singular.

Teorema 26.7 (teorema de Sochocki). Si zq es esencialmente singular, entonces el punto de la función f(z), entonces para cualquier número complejo L, incluyendo A = oh, existe una secuencia de puntos z n tal que z n -> zo y Lim f(zn) = A.

n->os

Prueba. Consideremos primero el caso Una = oh. En la primera parte de la demostración del Teorema 2G.2, establecimos que si f(z) está acotado en alguna vecindad perforada del punto r0, entonces todos los coeficientes c, norte = - 1, - 2,... de la parte principal son iguales a cero (y, en consecuencia, la singularidad en th es removible). Dado que, por supuesto, r0 es un punto esencialmente singular, la función f(r) es ilimitada en cualquier vecindad perforada del punto r0. Tomemos una vecindad estrecha 0 Z tal que f(zi) > 1 (si |/(r)| z - zo R/2 hay un punto z-2 , donde |/(dd)| > 2, etc.: en el barrio perforado O 71. Es obvio que rn -e go y lim /(r«) = oo. Por tanto, en el caso A = oo, Teorema 26.7

probado.

deja ahora una f oh. Supongamos primero que hay un vecindario perforado 0

= -yy---- será analítico en este vecindario perforado y, en consecuencia,

/(G) - A

en consecuencia, r es un punto singular aislado de la función Φ(r). Vamos a mostrar. que r0 es un punto esencialmente singular de Φ(r). Que esté mal. Entonces existe un límite lim Φ(r), ya sea finito o infinito. Porque

/(r) = A + , entonces Hsh /(r) también existe, lo que contradice la condición

F(g) ~ :-*z 0

vista del teorema. Por tanto, r0 es un punto esencialmente singular de la función Φ(r). Según lo demostrado anteriormente, existe una secuencia de puntos r n tal que r n o y lim Φ(r n) = oo. De aquí

Hemos demostrado la afirmación requerida bajo el supuesto de que f(r) F.A. en alguna vecindad perforada del punto r. Supongamos ahora que esto no es cierto, es decir en cualquier vecindad perforada arbitrariamente pequeña del punto th existe tal punto GRAMO", que f(r") = A. Entonces para cualquier PAG en la vecindad perforada 0 f(zu) = L. Por lo tanto, la afirmación requerida es verdadera PAG-yuo

en todos los casos, y se demuestra el teorema 26.7.

Según el teorema 26.7 (de Sokhotsky), en cualquier vecindad perforada (arbitrariamente pequeña) de un punto esencialmente singular, la función f(r) toma valores arbitrariamente cercanos a cualquier número en el plano complejo extendido C.

Para estudiar puntos singulares aislados, suelen resultar útiles las conocidas expansiones de Taylor de funciones elementales básicas.

EJEMPLO 2G.8. Determinar el tipo de punto singular zq = 0 para la función

Resuelto y e. Expandimos el numerador y denominador en una serie de Taylor en potencias de r. Sustituyendo en (22.11) 3 z en lugar de r y restar 1, obtenemos

Usando (22.12), obtenemos el desarrollo del denominador:

Las series en estos desarrollos convergen en todo el plano complejo €. Tenemos

y /2(2) son análogos en una vecindad del punto zo = 0 (e incluso en todo el plano) y /2(20) F 0, entonces h(z) también es analítico en alguna vecindad del punto gF 0. Según el Corolario 26.4, el punto Zo = 0 es el polo del orden norte = 4.

II ejemplo 26.9. Encontrar puntos singulares de una función f(z)= sin j - y determinar su tipo.

P e en e y e. La función tiene un único punto singular final. zq = 1. En otros puntos de C, la función w =--- analítico; de ahí la función pecado w será analítico.

Sustituyendo en el desarrollo del seno (22.12) - en lugar de r, obtenemos

Hemos obtenido la expansión de la función seno en una serie de Laurent en una vecindad perforada del punto 20 = 1. Dado que la expansión resultante contiene infinitos términos con potencias negativas (r - 1), entonces zq = 1 es un punto singular esencial (en este caso, la expansión de Laurent consta sólo de la parte principal y falta la parte correcta).

Tenga en cuenta que en este caso también fue posible establecer la naturaleza de la singularidad directamente a partir de la definición, sin recurrir a la expansión en serie. De hecho, hay secuencias (r") y (2") que convergen a zo= 1, y tal que f(z"n)= 1, /(2") = 0 (especifique dichas secuencias usted mismo). Entonces, f(z) no tiene límite cuando z-> 1 y de ahí el punto zq - 1 es esencialmente singular.

Introduzcamos el concepto de expansión de Laurent de una función en la vecindad de un punto. Zq = 00 y considere la conexión entre la expansión y la naturaleza de la singularidad en este punto. Tenga en cuenta que las definiciones de un punto singular aislado y su tipo (extraíble, polar o esencialmente singular) se trasladan al caso zq = oc sin cambios. Pero los teoremas 26.2. 26.3 y 26.6, relacionados con la naturaleza de las expansiones de Laurent, deben cambiarse. La cuestión es que los miembros c norte (z - 2o) pág. PAG= -1,-2,..., la parte principal, que define la "irregularidad" de la función cerca del punto final Zq, como 2 tiende a oo, se comportarán “correctamente” (tienden a 0). Por el contrario, los integrantes de la parte regular con PAG= 1,2,... tenderá a oo; determinan la naturaleza de la singularidad en Zq = oo. Por lo tanto, la mayor parte de la expansión en el vecindario de oo serán los términos con potencias positivas. PAG, y correcto - con negativo.

Introduzcamos una nueva variable. w = 12. Función televisión= 1/2, extendido de modo que u(oo) = 0, uno a uno y mapea conformemente la vecindad z > R puntos zq = 00 en la vecindad de |w| wq = 0. Si la función f(z) análisis en un barrio perforado R z Zq = oc, entonces la función G(w) = f(l/w) será analítico en el barrio amarillo 0 wo = 0. Dado que para 2 -> oo habrá w-> 0, entonces

Es por eso G(w) tiene en el punto wq = 0 es una singularidad del mismo tipo que f(z) en el punto Zq = 00. Expandamos la función G(w) en una serie de Laurent en una vecindad perforada del punto wo = 0:

Las sumas del lado derecho de (26.5) representan las partes correcta y principal del desarrollo, respectivamente. Pasemos a la variable. z, sustituyendo w = 1/z:

denotando PAG\u003d -A *, 6 * \u003d 6_ " \u003d Con p y notando que G(l/z) = f(z)), obtenemos

La descomposición (2G.G) se llama Expansión de Laurent de la función f(z) en una vecindad perforada del punto zq=oo. La primera suma en (2G.6) se llama parte derecha, y la segunda suma es parte principal esta descomposición. Dado que estas sumas corresponden a las partes correcta y principal del desarrollo (26.5), el desarrollo (26.6) satisface los análogos de los teoremas 26.2, 26.3 y 26.6. Por tanto, el siguiente teorema es análogo al teorema 26.2.

Teorema 26.10. Punto singular aisladozq - sistema operativo (funciones/(GRAMO) es removible si y solo si la expansión de Laurent en un vecindario perforado de este punto tiene la forma

t.s. consta sólo de la parte correcta.

Ponemos /(oo) = co. La función definida por la serie (26.7) que converge en la vecindad z > R puntos 2o \u003d oc, llamados analítica en el punto z o = oo. (Tenga en cuenta que esta definición es equivalente a la analiticidad de la función G(w) en el punto wo = 0.)

Ejemplo 26.11. Investiga el punto singular zq = oo de la función.

Como el límite es finito, entonces zo = oo es un punto singular removible de la función f(r). Si ponemos /(oo) = lim J(z)= 0, entonces f(z) se convertirá

tic en el punto Zo= os. Mostremos cómo encontrar el desarrollo correspondiente (26.7). Pasemos a la variable. w = 1 fz. Sustituyendo z= 1 /?e, obtenemos

(la última igualdad es válida en la vecindad perforada del punto w0 = 0, pero ampliaremos la definición (7(0) = 0). La función resultante tiene puntos singulares w =±yo, w =-1/3, y en el punto Wq = 0 es analítico. Función de expansión G(w) por grados w(como se hizo en el ejemplo 25.7) y sustituyendo en la serie de potencias resultante w = 1/z se puede obtener el desarrollo (26.7) de la función f(z).

Teorema 26.3 para el caso zo= oo se reescribirá de la siguiente forma.

Teorema 26.12. Punto singular aislado ir = os la función f(z) es un polo si y sólo si la parte principal del desarrollo de Laurent (26.6) tiene sólo un número finito de coeficientes distintos de cero Con":

Aquí la serie es la parte regular y el polinomio entre paréntesis es la parte principal de la expansión. La multiplicidad del polo en oc se define como la multiplicidad del polo. wq = 0 funciones G(z). Es fácil ver que la multiplicidad del polo coincide con el número norte en (26.8).

Q p | (yo 2 + 1) (z + 3) 2

Tarea. Demuestre que la función f(z)) =-- -- tiene en

punto zo = oo orden de polos 3.

Se reescribe el teorema 26.6 sobre un punto singular esencial para el caso zo= os casi palabra por palabra, y no nos detenemos en ello en detalle.

Conceptos básicos y definiciones:

El cero de la función analítica f(z) es el punto “a” para el cual f(a)=0.

El cero de orden “n” de la función f(z) es el punto “a” si pero fn(a)¹0.

Un punto singular "a" se denomina punto singular aislado de la función f(z) si existe una vecindad de este punto donde no hay puntos singulares distintos de "a".

Los puntos singulares aislados son de tres tipos: .

1 puntos especiales extraíbles;

3 puntos singulares esenciales.

El tipo de punto singular se puede determinar en función del comportamiento de la función dada en el punto singular encontrado, así como de la forma de la serie de Laurent obtenida para la función en la vecindad del punto singular encontrado.

Determinar el tipo de un punto singular por el comportamiento de la función en él.

1. Puntos Singulares Removibles.

Un punto singular aislado a de la función f(z) se llama removible si existe un límite finito.

2. Polacos.

Un punto singular aislado a de la función f(z) se llama polo si .

3. Puntos singulares significativos.

Un punto singular aislado a de una función f(z) se llama punto singular esencial si no existe ni finito ni infinito.

La siguiente relación tiene lugar entre los ceros y los polos de la función.

Para que un punto a sea un polo de orden n de la función f(Z), es necesario y suficiente que ese punto sea un cero de orden n para la función .

Si n=1 el polo se llama simple.

Definición: Un punto singular aislado de un carácter de un solo valor se llama:

a) removible si la parte principal de la descomposición está ausente;

b) un poste si la parte principal contiene un número finito de miembros;

c) un punto esencialmente singular si la parte principal contiene un número infinito de términos.

a) Así, en la vecindad de un punto singular removible, la expansión tiene la forma:

expresa la función en todos los puntos del círculo |z-a|

En el centro z=a, la igualdad es falsa, porque la función en z=a tiene una discontinuidad y el lado derecho es continuo. Si se cambia el valor de la función en el centro, tomándolo igual al valor del lado derecho, entonces se eliminará el espacio, de ahí el nombre, removible.

b) En una vecindad de un polo de orden m, el desarrollo en serie de Laurent tiene la forma:

c) En las proximidades de un poste simple

Deducciones y fórmulas para su cálculo.

El residuo de una función analítica f(z) en un punto singular aislado z 0 es un número complejo igual al valor de la integral , tomada en la dirección positiva a lo largo del círculo L centrado en el punto z 0 , que se encuentra en la región de analiticidad de la función f(z) (es decir, en el anillo 0<|z-z0|

El residuo de la función f(z) en un punto singular aislado z 0 se denota con el símbolo Res f(z 0) o Res (f(z); z 0). De este modo,

Resf(z0)= . (22.15.1)

Si ponemos n=-1 en la fórmula (22.15.1), obtenemos:

C-1=

o Res f(z 0)= C -1 ,

aquellos. el residuo de la función f(z) con respecto al punto singular z 0 es igual al coeficiente del primer término con exponente negativo en el desarrollo de la función f(z) en una serie de Laurent.

Cálculo de deducciones.

Puntos singulares regulares o removibles. Obviamente, si z=z 0 es un punto singular regular o removible de la función f(z), entonces Res f(z 0)=0 (no hay parte principal en la descomposición de Laurent en estos casos, por lo que c-1= 0).

Polo. Sea el punto z 0 un polo simple de la función f(z). Entonces la serie de Laurent para la función f(z) en una vecindad del punto z 0 tiene la forma:

De aquí

Por lo tanto, pasando esta igualdad al límite como z --z 0 , obtenemos

Resf(z0)=

Punto esencialmente especial. Si el punto z 0 es un punto esencialmente singular de la función f(z), entonces para calcular el residuo de la función en este punto, normalmente se determina directamente el coeficiente c-1 en el desarrollo de la función en una serie de Laurent.

Clasificación de eventos. Suma, producto de eventos, sus propiedades, representación gráfica.

Los eventos se dividen en:

1. Aleatorio

2. Creíble

3. Imposible

Confiable: este es un evento que necesariamente ocurre en estas condiciones (a la noche le sigue la mañana).

Aleatorio es un evento que puede ocurrir o no (aprobar un examen).

Lo imposible es un evento que no ocurrirá bajo las condiciones dadas (saca un lápiz verde de la caja con solo los rojos).

punto singular

en matemáticas.

1) Punto singular de la curva dada por la ecuación F ( x,y) = 0, - punto M 0 ( x 0 , y 0), en el que ambas derivadas parciales de la función F ( x,y) desaparecer:

Si, además, no todas las segundas derivadas parciales de la función F ( x,y) en el punto M 0 son iguales a cero, entonces O. t. se llama doble. Si, junto con la desaparición de las primeras derivadas en el punto M 0, todas las segundas derivadas desaparecen, pero no todas las terceras derivadas son iguales a cero, entonces el O. t. se llama triple, y así sucesivamente. Al estudiar la estructura de una curva cerca de un doble O. t., el signo de la expresión juega un papel importante

Si Δ > 0, entonces el O.t. se llama aislado; por ejemplo, la curva y 2 - x 4 + 4x 2= 0 el origen es un O. t. aislado (ver arroz. 1 ). Si Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - un 4= 0 el origen de coordenadas es el O. t. nodal (ver arroz. 2 ). Si Δ = 0, entonces la curva O.t. está aislada o se caracteriza por el hecho de que diferentes ramas de la curva tienen una tangente común en este punto, por ejemplo: tangente y forman un punto, como una curva. y2-x3= 0 (ver arroz. 3 , a); b) cúspide de segundo tipo: diferentes ramas de la curva se encuentran en el mismo lado de la tangente común, como una curva (y-x2)2-x5= 0 (ver arroz. 3 , b); c) punto de autocontacto (para una curva y2-x4= 0 origen es un punto de autocontacto; (cm. arroz. 3 , V). Junto con el O.t. especificado, hay muchos otros O.t. con nombres especiales; por ejemplo, un punto asintótico es el vértice de una espiral con un número infinito de vueltas (ver Fig. arroz. 4 ), punto de quiebre, punto de esquina, etc.

2) Un punto singular de una ecuación diferencial es un punto en el que tanto el numerador como el denominador del lado derecho de la ecuación diferencial desaparecen simultáneamente (ver Ecuaciones diferenciales).

donde P y Q son funciones continuamente diferenciables. Suponiendo O. t. ubicado en el origen de coordenadas y usando la fórmula de Taylor (Ver fórmula de Taylor), podemos representar la ecuación (1) en la forma

donde P 1 ( x,y) y P 1 ( x,y) son infinitesimales con respecto a

Es decir, si λ 1 ≠ λ 2 y λ 1 λ 2 > 0 o λ 1 = λ 2, entonces O. t. es un nodo; todas las curvas integrales que pasan por puntos de una vecindad suficientemente pequeña del nodo entran en él. Si λ 1 ≠ λ 2 y λ 1 λ 2 i β, α ≠ 0 y β ≠ 0, entonces O. t. es un foco; todas las curvas integrales que pasan por puntos en una vecindad suficientemente pequeña del foco son espirales con un número infinito de vueltas en cualquier vecindad arbitrariamente pequeña del foco. Si, finalmente, λ 1,2 = ± iβ, β ≠ 0, entonces el carácter de O. t. no está determinado por términos lineales en expansiones de P ( x,y) y Q ( x,y), como ocurrió en todos los casos anteriores; aquí O.t. puede ser un foco o centro, o puede tener un carácter más complejo. En la vecindad del centro, todas las curvas integrales son cerradas y contienen el centro dentro de ellas. Entonces, por ejemplo, el punto (0, 0) es un nodo para las ecuaciones en" = 2u/x(λ 1 = 1, λ 2 = 2; ver arroz. 5 , a) y y" = u/x(λ 1 = λ 2 = 1; ver arroz. 5 , b), una silla para la ecuación y" = -y/x(λ 1 = -1, λ 2 = 1 ; cm. arroz. 6 ), el foco de la ecuación y" =(x + y) / (x - y) (λ 1 = 1 - i, λ 2 = 1 + i; cm. arroz. 7 ) y el centro de la ecuación y" = -x/y(λ1 = -i, λ2 = i; cm. arroz. 8 ).

Si x, y) y Q ( x,y) son analíticos, la vecindad de un O. t. de orden superior se puede dividir en regiones: D 1 - llena de curvas integrales, ambos extremos entran en el O. t. (regiones elípticas), D 2 - llena de curvas integrales, un extremo ingresa al O. t. (regiones parabólicas), y D 3 - regiones delimitadas por dos curvas integrales incluidas en el O. t., entre las cuales hay curvas integrales del tipo de hipérbolas (regiones hiperbólicas) (ver. arroz. 9 ). Si no hay curvas integrales que entren en un punto O., entonces el punto O. se llama punto de tipo estable. La vecindad de un O. t. estable consta de curvas integrales cerradas que contienen O. t. dentro de sí mismas, entre las cuales se ubican espirales (ver Fig. arroz. 10 ).

El estudio de las ecuaciones diferenciales de O. t., es decir, en esencia, el estudio del comportamiento de familias de curvas integrales en una vecindad de O. t. M. Lyapunov a, A. Poincaré y otros).

3) Un punto singular de una función analítica de un solo valor es un punto en el que se viola la analiticidad de la función (ver Funciones analíticas). Si hay un barrio de O. t. a, libre de otros O. t., entonces el punto A se llama aislado O. t. Si A es un T.O. aislado y existe un T.O. finito se llama T.O. removible Cambiando apropiadamente la definición de la función en el punto a (o redefiniéndola en este punto, si la función no está definida en absoluto en ese punto), es decir, estableciendo F(a)= segundo, es posible lograr a se convertirá en un punto ordinario de la función corregida. Por ejemplo, punto z= 0 es un OT removible para la función f 1 ( z) = F(z), Si z≠ 0, y F 1(0),=1, punto z= 0 es un punto ordinario [ F 1 (z) es analítico en el punto z= 0]. Si A- aislado O. t. y a se llama polo o punto inesencialmente singular de la función F(z), si la serie Laurent) funciona F(z) en una vecindad de un O.t. aislado no contiene poderes negativos z-a, Si A- O. t. extraíble, contiene un número finito de poderes negativos z-a, Si A- polo (en este caso, el orden del polo R se define como la potencia más alta de a - un punto esencialmente singular. Por ejemplo, para la función

pag = 2, 3,…)

punto z= 0 es el polo del orden R, para la función

punto z= 0 es un punto singular esencial.

En el límite del círculo de convergencia de una serie de potencias debe haber al menos un O. t. de la función representada dentro de este círculo por la serie de potencias dada. Todos los puntos límite del dominio de existencia de una función analítica de un solo valor (límite natural) son puntos límite de esta función. Por tanto, todos los puntos del círculo unitario | z| = 1 son especiales para la función

Para una función analítica multivaluada, el concepto de "O. T." más difícil. Además del O.t., en hojas individuales de la superficie de Riemann de una función (es decir, el O.t. de elementos analíticos univaluados), cualquier punto de ramificación es también un O.t. de la función. Los puntos de ramificación aislados de una superficie de Riemann (es decir, puntos de ramificación tales que en algunas de sus vecindades no hay otras funciones O.t. en ninguna hoja) se clasifican de la siguiente manera. Si a es un punto de ramificación aislado de orden finito y existe un a finito, se llama polo crítico. Si A es un punto de ramificación aislado de orden infinito, y a se llama O. t trascendental. Todos los demás puntos de ramificación aislados se denominan puntos críticos esencialmente singulares. Ejemplos: punto z= 0 es un punto crítico ordinario de la función f ( z) = iniciar sesión z y un punto singular esencial crítico de la función F (z) = registro de pecado z.

Cualquier O.t., excepto uno removible, es un obstáculo para la continuación analítica, es decir, la continuación analítica a lo largo de una curva que pasa por un O.t. inamovible es imposible.

Gran enciclopedia soviética. - M.: Enciclopedia soviética. 1969-1978 .

Vea qué es "Punto especial" en otros diccionarios:

Puntos aquí. Véase también punto singular (ecuaciones diferenciales). Una característica o singularidad en matemáticas es un punto en el que un objeto matemático (generalmente una función) no está definido o tiene un comportamiento irregular (por ejemplo, un punto en el que... ... Wikipedia

Una función analítica es un punto en el que se violan las condiciones de analiticidad. Si una función analítica f(z) se define en alguna vecindad del punto z0 en todas partes... Enciclopedia Física

Una función analítica es un punto en el que se viola la analiticidad de una función... Gran diccionario enciclopédico

punto singular- — [Ya.N. Luginsky, M.S. Fezi Zhilinskaya, Yu.S. Kabirov. Diccionario inglés ruso de ingeniería eléctrica e industria energética, Moscú, 1999] Temas de ingeniería eléctrica, conceptos básicos EN punto singular ... Manual del traductor técnico

1) Una OT de una función analítica f(z) es un obstáculo para la continuación analítica de un elemento de la función f(z) de una variable compleja z a lo largo de algún camino en el plano de esta variable. Dejemos que la función analítica f(z) esté definida por algunos... ... Enciclopedia Matemática

Una función analítica, el punto en el que se viola la analiticidad de la función. * * * PUNTO SINGULAR UN PUNTO SINGULAR de una función analítica, un punto en el que se viola la analiticidad de la función... diccionario enciclopédico

punto singular- ypatingasis taškas statusas T sritis automatika atitikmenys: engl. punto singular vok. singularer Punkt, m rus. punto singular, fpranc. partícula puntual, m; punto singular, m … Automatikos terminų žodynas

punto singular- ypatingasis taškas statusas T sritis fizika atitikmenys: engl. punto singular vok. singularer Punkt, m rus. punto singular, fpranc. punto singular, m … Fizikos terminų žodynas

Las series de Taylor sirven como una herramienta eficaz para estudiar funciones analíticas en el círculo zol. Para estudiar funciones analíticas en una región anular, resulta que es posible construir expansiones en potencias positivas y negativas (z - zq) de la forma que generaliza las expansiones de Taylor. La serie (1), entendida como la suma de dos series, se denomina serie de Laurent. Es claro que la región de convergencia de la serie (1) es la parte común de las regiones de convergencia de cada una de las series (2). Encontrémosla. El área de convergencia de la primera serie es un círculo cuyo radio está determinado por la fórmula de Cauchy-Hadamard. Dentro del círculo de convergencia, la serie (3) converge a una función analítica, y en cualquier círculo de menor radio, converge absolutamente y uniformemente. La segunda serie es una serie de potencias con respecto a la variable. La serie (5) converge dentro de su círculo de convergencia a una función analítica de la variable compleja m - * oo, y en cualquier círculo de menor radio converge absoluta y uniformemente, lo que significa que la región de convergencia de la serie (4) es la apariencia del círculo - Si entonces hay una región de convergencia común de las series (3) y (4) - un anillo circular en el que la serie (1) converge a una función analítica. Además, en cualquier anillo converge absoluta y uniformemente. Ejemplo 1. Determinar la región de convergencia de la serie de rad Laurent Los puntos singulares aislados y su clasificación (z), que es univaluada y apolítica en un anillo circular, se pueden representar en este anillo como la suma de una serie convergente cuyos coeficientes Cn están determinados y calculados de forma única mediante las fórmulas donde 7p es un círculo de radio m. Fijemos un punto arbitrario z dentro del anillo R. Construimos círculos con centros en el punto r0 cuyos radios satisfacen las desigualdades y consideramos un nuevo anillo. De acuerdo con el teorema integral de Cauchy para un dominio múltiplemente conexo, transformamos cada una de las integrales en la suma (8) por separado. Para todos los puntos £ a lo largo del círculo 7d*, se satisface la relación de la suma de una serie uniformemente convergente 1 1. Por lo tanto, la fracción ^ se puede representar en vi- /" / Para todos los puntos £ en el círculo ir> la relación se cumple Por lo tanto, la fracción ^ se puede representar como la suma de una serie uniformemente convergente en las fórmulas (10) y (12) son funciones analíticas en un anillo circular. Por lo tanto, según el teorema de Cauchy, los valores de las integrales correspondientes no cambian si los círculos 7/r y 7r/ se reemplazan por cualquier círculo. Esto nos permite combinar las fórmulas (10) y (12). Reemplazando las integrales del lado derecho de la fórmula (8) con sus expresiones (9) y (11), respectivamente, obtenemos la expansión deseada. Dado que z es un valor arbitrario punto del anillo, se sigue que la serie (14) converge a la función f(z) en todas partes de este anillo, y en cualquier anillo la serie converge a esta función de manera absoluta y uniforme. Demostremos ahora que la descomposición de la forma (6) es única. Suponiendo que se produce una descomposición más, entonces, en todo el interior del anillo R, tenemos En la circunferencia, la serie (15) converge uniformemente. Multiplicamos ambos lados de la igualdad (donde m es un número entero fijo e integramos ambas series término por término. Como resultado, obtenemos Csh en el lado izquierdo y en el derecho. Por lo tanto, (4, = St. Dado que m es un número arbitrario, entonces la última serie de igualdad (6), cuyos coeficientes se calculan mediante las fórmulas (7), se denomina serie de Laurent de la función f(z) en el anillo 7) para los coeficientes de la serie de Laurent. rara vez se utilizan en la práctica porque, por regla general, requieren cálculos engorrosos. Generalmente, si es posible, se utilizan expansiones de Taylor de funciones elementales ya preparadas. Basado en la unicidad de la expansión, cualquier método legítimo conduce al mismo resultado. Ejemplo 2 Considere las expansiones en serie de Laurent de funciones en diferentes dominios, suponiendo que Fuiscius /(r) tiene dos puntos singulares: Por lo tanto, hay tres dominios anulares, centrados en el punto r = 0. En cada uno de los cuales la función /(r) es analítico: a ) círculo anillo la apariencia del círculo (Fig. 27). Encontremos las expansiones de Laurent de la función /(z) en cada una de estas regiones. Representamos /(z) como una suma de fracciones elementales a) Relación de transformación circular (16) de la siguiente manera Usando la fórmula para la suma de los términos de una progresión geométrica, obtenemos b) El anillo para la función -z permanece convergente en este anillo, ya que la Serie (19) para la función j^j para |z| > 1 diverge. Por tanto, transformamos la función /(z) de la siguiente manera: aplicando nuevamente la fórmula (19), obtenemos que esta serie converge para. Sustituyendo las expansiones (18) y (21) en la relación (20), obtenemos c) La exterioridad del círculo para la función -z con |z| > 2 diverge, y la serie (21) para la función Representemos la función /(z) de la siguiente forma: /<*>Usando las fórmulas (18) y (19), obtenemos OR 1. Este ejemplo muestra que para la misma función f(z) la expansión de Laurent, en términos generales, tiene diferente tipo para diferentes anillos. Ejemplo 3. Encuentre la descomposición de las 8 series de Laurent de la función Serie de Laurent Puntos singulares aislados y su clasificación en la región anular A Usamos la representación de la función f (z) de la siguiente forma: y transformamos el segundo término usando la fórmula para la suma de los términos de una progresión geométrica, obtenemos Al sustituir las expresiones encontradas en la fórmula (22), tenemos el Ejemplo 4. Expandir la función en una serie de Laurent en la vecindad de zq = 0. Para cualquier complejo , tenemos Let Esta expansión es válida para cualquier punto z Ф 0. En este caso, la región anular es todo el plano complejo con un punto z eliminado - 0. Esta región se puede definir mediante la siguiente relación: Esta función es analítica en la región A partir de las fórmulas (13) para los coeficientes de la serie de Laurent, siguiendo el mismo razonamiento que en el párrafo anterior, se pueden obtener las desigualdades de Kouiw. si la función f(z) está acotada en un círculo, donde M es una constante), entonces puntos singulares aislados Un punto zo se llama punto singular aislado de la función f(z) si existe una vecindad anular del punto ( este conjunto a veces también se denomina vecindad perforada del punto 2o), en donde la función f(z) es univaluada y analítica. En el propio punto zo, la función o no está definida o no es univaluada ni analítica. Se distinguen tres tipos de puntos singulares en función del comportamiento de la función /(z) al aproximarse al punto zo. Un punto singular aislado se llama: 1) removible si existe un finito 2) pmusach si 3) un punto esencialmente singular si la función f(z) no tiene límite para Teorema 16. Un punto singular aislado z0 de una función f(z) es un punto singular removible si y sólo si la expansión de Laurent de la función f(z) en una vecindad del punto zo no contiene una parte principal, es decir, tiene la forma Let zo - punto singular removible. Entonces existe uno finito y, por tanto, la función f(z) está acotada en una vecindad prológica del punto r. En virtud de las desigualdades de Cauchy, establecemos que p es posible elegir arbitrariamente pequeño, entonces todos los coeficientes en valores negativos las potencias (z - 20) son iguales a cero: Por el contrario, supongamos que la expansión de Laurent de la función /(r) en una vecindad del punto zq contiene sólo la parte correcta, es decir, tiene la forma (23) y, por tanto , es Taylor. Es fácil ver que para z -* z0 la función /(z) tiene un valor límite: Teorema 17. Un punto singular aislado zq de la función f(z) es removible si y sólo si la función J(z) es delimitado en algún barrio perforado del punto zq, Zgmechai no. Sea r0 un punto singular removible de f(r). Suponiendo que obtenemos que la función f(r) es analítica en algún círculo centrado en el punto th. Esto determina el nombre del punto: desechable. Teorema 18. Un punto singular aislado zq de una función f(z) es un polo si y sólo si la parte principal del desarrollo de Laurent de la función f(z) en una vecindad del punto contiene un número finito (y positivo) de términos distintos de cero, es decir, tiene la forma 4 Sea z0 un polo. Desde entonces existe una vecindad perforada del punto z0 en la que la función f(z) es analítica y distinta de cero. Entonces se define una función analítica en esta vecindad y, por lo tanto, el punto zq es un punto singular removible (cero) de la función o donde h(z) es una función analítica, h(z0) ∩ 0. es analítica en una vecindad del punto zq, y por tanto, de donde obtenemos que Supongamos ahora que la función f(z) tiene una descomposición de la forma (24) en una vecindad perforada del punto zo. Esto significa que en esta vecindad la función f(z) es analítica junto con la función. Para la función g(z), la expansión es válida de la cual está claro que zq es un punto singular removible de la función g(z) y existe Entonces la función tiende a 0 - el polo de la función Hay uno más simple hecho. El punto Zq es un polo de la función f(z) si y sólo si la función g(z) = y puede extenderse a una función analítica en una vecindad del punto zq estableciendo g(z0) = 0. El orden del polo de la función f(z) se llama orden de cero de la función jfa. Los teoremas 16 y 18 implican la siguiente afirmación. Teorema 19. Un delgado singular aislado es esencialmente singular si y sólo si la parte principal de la expansión de Laurent en una vecindad perforada de este punto contiene infinitos términos distintos de cero. Ejemplo 5. El punto singular de la función es zo = 0. Tenemos Serie Laurent Puntos singulares aislados y su clasificación Por lo tanto, zo = 0 es un punto singular removible. El desarrollo de la función /(z) en una serie de Laurent en las proximidades del punto cero contiene sólo la parte correcta: Ejemplo 7. f(z) = El punto singular de la función f(z) es zq = 0. Considere el comportamiento de esta función en los ejes real e imaginario: en el eje real en x 0, en el eje imaginario Por lo tanto, ni finito ni El límite infinito f(z) en z -* 0 no existe. Por tanto, el punto r0 = 0 es un punto esencialmente singular de la función f(z). Encontremos la expansión de Laurent de la función f(z) en una vecindad del punto cero. Para cualquier complejo C que tenemos establecemos. Entonces la expansión de Laurent contiene un número infinito de términos con potencias negativas de z.