Modelli descritti da sistemi di due autonomi equazioni differenziali.

piano di fase. Ritratto di fase. metodo isoclino. principali isocline. Stabilità dello stato stazionario. Sistemi lineari. Tipi di punti chiave: nodo, sella, fuoco, centro. Esempio: reazioni chimiche primo ordine.

I risultati più interessanti sulla modellazione qualitativa delle proprietà dei sistemi biologici sono stati ottenuti su modelli di due equazioni differenziali, che consentono uno studio qualitativo utilizzando il metodo piano di fase. Consideriamo un sistema di due equazioni differenziali ordinarie autonome della forma generale

(4.1)

P(x,y), Q(x,y)- funzioni continue definite in qualche dominio G Piano euclideo ( x,y- Coordinate cartesiane) e avente in quest'area derivate continue di ordine non inferiore alla prima.

Regione G può essere illimitato o limitato. Se variabili x, y hanno un significato biologico specifico (concentrazioni di sostanze, abbondanza di specie), molto spesso l'area Gè il quadrante positivo del semipiano destro:

0 £ X< ¥ ,0 £ sì< ¥ .

Le concentrazioni di sostanze o l'abbondanza di specie possono anche essere limitate dall'alto dal volume del vaso o dalla superficie dell'habitat. Quindi l'intervallo di variabili ha la forma:

0 £ X< x 0 , 0 £ sì< y 0 .

Variabili x, y cambiamento nel tempo secondo il sistema di equazioni (4.1), in modo che ogni stato del sistema corrisponda a una coppia di valori di variabili ( x, y).

Viceversa, per ogni coppia di variabili ( x, y) corrisponde ad un certo stato del sistema.

Considera un piano con assi di coordinate su cui sono tracciati i valori delle variabili x,y. Ogni punto M questo piano corrisponde ad un certo stato del sistema. Tale piano è chiamato piano di fase e rappresenta la totalità di tutti gli stati del sistema. Il punto M(x, y) è detto punto raffigurante o rappresentante.

Lasciamo che sia il momento iniziale t=t 0 che rappresenta le coordinate del punto M 0 (X(T 0), sì(T 0)). In ogni momento successivo T il punto raffigurante si sposterà in base alle variazioni dei valori delle variabili X(T), sì(T). Insieme di punti M(X(T), y(t)) sul piano delle fasi, la cui posizione corrisponde agli stati del sistema in procinto di cambiare variabili nel tempo x(t), y(t) secondo le equazioni (4.1), viene chiamato traiettoria di fase.

L'insieme delle traiettorie di fase per diversi valori iniziali delle variabili fornisce un "ritratto" facilmente visibile del sistema. Edificio ritratto di fase consente di trarre conclusioni sulla natura dei cambiamenti nelle variabili x, y senza conoscere le soluzioni analitiche del sistema di equazioni originale(4.1).

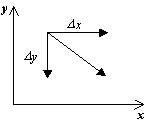
Per rappresentare un ritratto di fase, è necessario costruire un campo vettoriale di direzioni per le traiettorie del sistema in ciascun punto del piano di fase. Specificando un incrementoD t>0,otteniamo gli incrementi corrispondenti D X E D sì dalle espressioni:

D x=P(x,y)D T,

D y=Q(x,y)D T.

direzione del vettore dy/dx nel punto ( x, y) dipende dal segno delle funzioni P(x, y), Q(x, y) e può essere dato da una tabella:

P(x,y)>0,Q(x,y)>0
P(x,y)<0,Q(x,y)<0
P(x,y)>0,Q(x,y)<0
P(x,y)<0,Q(x,y)>0

.(4.2)

Soluzione a questa equazione y=y(x, c), o implicitamente F(x,y)=c, Dove Conè la costante di integrazione, fornisce la famiglia delle curve integrali dell'equazione (4.2) - traiettorie di fase sistema (4.1) sull'aereo x, y.

Metodo isoclino

Per costruire un ritratto di fase, si usa metodo isoclino - sul piano di fase vengono disegnate linee che intersecano le curve integrali con un angolo specifico. L'equazione isoclina è facile da ottenere dalla (4.2). Mettiamo

Dove UN– una certa costante. Senso UN rappresenta la tangente della pendenza della tangente alla traiettoria della fase e può assumere valori da -¥ a + ¥ . Sostituendo invece di dy/dx in (4.2) la quantità UN otteniamo l'equazione isoclina:

.(4.3)

L'equazione (4.3) determina in ogni punto del piano l'unica tangente alla corrispondente curva integrale, ad eccezione del punto in cui P(x,y)= 0, Q (x,y) = 0 , in cui la direzione della tangente diventa indefinita, poiché il valore della derivata diventa indefinito:

.

Questo punto è il punto di intersezione di tutte le isocline - punto speciale. Contemporaneamente annulla le derivate temporali delle variabili X E sì.

Pertanto, nel punto singolare, i tassi di variazione delle variabili sono pari a zero. Pertanto, il punto singolare delle equazioni differenziali delle traiettorie di fase (4.2) corrisponde a stato stazionario del sistema(4.1), e le sue coordinate sono i valori stazionari delle variabili x, y.

Di particolare interesse sono principali isocline:

dy/dx=0, P(x,y)=0 – isoclina delle tangenti orizzontali e

dy/dx=¥ , Q(x,y)=0 – isoclina delle tangenti verticali.

Costruendo le principali isocline e trovando il punto della loro intersezione (x,y), le cui coordinate soddisfano le condizioni:

troveremo così il punto di intersezione di tutte le isocline del piano di fase, in cui la direzione delle tangenti alle traiettorie di fase è indefinita. Questo - punto singolare, che corrisponde stato stazionario del sistema(Fig. 4.2).

Il sistema (4.1) ha tanti stati stazionari quanti sono i punti di intersezione delle isocline principali sul piano delle fasi.

Ciascuna traiettoria di fase corrisponde a un insieme di movimenti di un sistema dinamico che passa attraverso gli stessi stati e differisce tra loro solo per l'inizio del riferimento temporale.

Se le condizioni del teorema di Cauchy sono soddisfatte, allora attraverso ogni punto dello spazio x, y, t passa attraverso un'unica curva integrale. Lo stesso vale, grazie all'autonomia, per le traiettorie di fase: per ogni punto del piano di fase passa un'unica traiettoria di fase.

Stabilità dello stato stazionario

Lasciamo che il sistema sia in equilibrio.

Allora il punto rappresentativo si trova in uno dei punti singolari del sistema, in cui, per definizione:

.

Se un punto singolare è stabile o meno è determinato dal fatto che il punto rappresentativo si allontani o meno con una piccola deviazione dallo stato stazionario. Applicato a un sistema di due equazioni, la definizione di stabilità nel linguaggioe, Dcome segue.

Lo stato di equilibrio è stabile se per ogni data area si discostano dallo stato di equilibrio (e )è possibile specificare l'area D (e ), che circonda lo stato di equilibrio e ha la proprietà che nessuna traiettoria abbia inizio all'interno della regione D , non raggiungerà mai il confine e . (figura 4.4)

Per un'ampia classe di sistemi: sistemi grezzi – la cui natura del comportamento non cambia con un piccolo cambiamento nel tipo di equazioni, le informazioni sul tipo di comportamento in prossimità dello stato stazionario possono essere ottenute studiando non l'originale, ma quello semplificato linearizzato sistema.

Sistemi lineari.

Considera un sistema di due equazioni lineari:

.(4.4)

Qui a, b, c, d- costanti, x, y- Coordinate cartesiane sul piano delle fasi.

La soluzione generale verrà cercata nella forma:

.(4.5)

Sostituisci queste espressioni nella (4.4) e riduci di e l T:

(4.6)

Sistema algebrico di equazioni (4.6) con incognite A, B ha soluzione diversa da zero solo se il suo determinante, composto dai coefficienti delle incognite, è uguale a zero:

.

Espandendo questo determinante, otteniamo l’equazione caratteristica del sistema:

.(4.7)

La soluzione di questa equazione fornisce i valori dell'indicatorel 1,2 , sotto il quale sono possibili valori diversi da zero UN E B soluzioni dell'equazione (4.6). Questi valori sono

.(4.8)

Se l'espressione radicale è negativa, alloral 1,2 numeri coniugati complessi. Supponiamo che entrambe le radici dell'equazione (4.7) abbiano parte reale diversa da zero e che non vi siano radici multiple. Allora la soluzione generale del sistema (4.4) può essere rappresentata come una combinazione lineare di esponenti con esponentil 1 , l 2 :

(4.9)

Per analizzare la natura delle possibili traiettorie del sistema sul piano di fase, utilizziamo trasformazione lineare omogenea delle coordinate, che porterà il sistema a forma canonica:

,(4.10)

che consente una rappresentazione sul piano delle fasi più conveniente rispetto al sistema originale (4.4). Introduciamo nuove coordinateξ , η secondo le formule:

(4.1)

È noto dal corso di algebra lineare che se le parti reali non sono uguali a zerol 1 , l 2 il sistema originale (4.4) con l'aiuto delle trasformazioni (4.11) può sempre essere trasformato nella forma canonica (4.10) e se ne può studiare il comportamento sul piano delle fasiξ , η . Consideriamo i vari casi che possono presentarsi qui.

Radici λ 1 , λ 2 – validi e dello stesso segno

In questo caso i coefficienti di trasformazione sono reali, ci muoviamo dal piano realex,yal piano reale ξ, η. Dividendo la seconda delle equazioni (4.10) per la prima, otteniamo:

.(4.12)

Integrando questa equazione, troviamo:

Dove .(4.13)

Accettiamo di intenderlo per λ 2 la radice dell'equazione caratteristica con un modulo grande, che non viola la generalità del nostro ragionamento. Allora, poiché nel caso in esame le radici λ 1 , λ2 – validi e dello stesso segno,UN>1 , e si tratta di curve integrali di tipo parabolico.

Tutte le curve integrali (tranne l'asse η , che corrisponde a ) toccano all'origine dell'asse ξ, che è anche una curva integrale dell'equazione (4.11). L'origine delle coordinate è un punto singolare.

Cerchiamo ora di determinare la direzione del moto del punto rappresentativo lungo le traiettorie di fase. Se λ 1, λ2 sono negativi, allora, come si vede dalle equazioni (4.10), |ξ|, |η| diminuire nel tempo. Il punto che rappresenta si avvicina all'origine, ma non la raggiunge mai. Altrimenti ciò contraddirebbe il teorema di Cauchy, il quale afferma che per ogni punto del piano delle fasi passa solo una traiettoria di fase.

Un punto così singolare attraverso il quale passano le curve integrali, proprio come una famiglia di parabole passa per l'origine, è chiamato nodo (Fig. 4.5)

Stato di equilibrio di tipo nodoso a λ 1, λ2 < 0 è stabile secondo Lyapunov, poiché il punto rappresentativo si muove lungo tutte le curve integrali verso l'origine delle coordinate. Questo nodo stabile. Se λ 1, λ2 > 0, allora |ξ|, |η| aumentano con il tempo e il punto rappresentativo si allontana dall'origine. In questo caso, il punto singolare– nodo instabile .

Sul piano di fase x, y resterà il carattere qualitativo generale del comportamento delle curve integrali, ma le tangenti alle curve integrali non coincideranno con gli assi coordinati. L'angolo di inclinazione di queste tangenti sarà determinato dal rapporto dei coefficienti α , β , γ , δ nelle equazioni (4.11).

Radici λ 1 , λ 2 sono validi e hanno segni diversi.

Converti da coordinate x,y alle coordinate ξ, η ancora una volta reale. Le equazioni per le variabili canoniche hanno ancora la forma (4.10), ma ora i segni λ 1, λ2 diverso. L'equazione della traiettoria di fase ha la forma:

Dove , (4.14)

Integrando (4.14), si trova

(4.15)

Questo L'equazione definisce una famiglia di curve di tipo iperbolico, dove entrambi gli assi coordinano sono gli asintoti (at UN=1 avremmo una famiglia di iperboli isoscele). Anche in questo caso gli assi delle coordinate sono curve integrali– queste saranno le uniche curve integrali passanti per l'origine. Ognidi cui è costituito da tre traiettorie di fase: di due movimenti verso uno stato di equilibrio (o allontanamento da uno stato di equilibrio) e da uno stato di equilibrio. Tutte le altre curve integrali– sono iperboli che non passano per l'origine (Fig. 4.6) Questo punto singolare si chiama "sella ». Le linee di livello vicino alla sella della montagna si comportano come traiettorie di fase in prossimità della sella.

Consideriamo la natura del movimento del punto rappresentativo lungo traiettorie di fase vicine allo stato di equilibrio. Lasciamo, ad esempio,λ 1 >0 , λ 2<0 . Quindi il punto rappresentativo posto sull'asse ξ , si allontanerà dall'origine e si posizionerà sull'asse η – si avvicinerà indefinitamente all'origine delle coordinate, senza raggiungerlo in un tempo finito. Dovunque si trovi il punto rappresentante nel momento iniziale (ad eccezione del punto singolare e dei punti sull'asintoto η =0), col tempo si allontanerà dallo stato di equilibrio, anche se all'inizio si muove lungo una delle curve integrali verso un punto singolare.

E' ovvio il punto singolare a sella è sempre instabile . Solo in condizioni iniziali appositamente scelte sull'asintotoη =0 il sistema si avvicinerà ad uno stato di equilibrio. Tuttavia, ciò non contraddice l’affermazione secondo cui il sistema è instabile. Se conti, che tutti gli stati iniziali del sistema sul piano di fase sono ugualmente probabili, allora la probabilità di tale stato iniziale che corrisponde al movimento nella direzione A il punto singolare è uguale a zero. Pertanto, qualsiasi movimento reale allontanerà il sistema dallo stato di equilibrio.Torniamo alle coordinatex,y,otteniamo la stessa immagine qualitativa della natura del movimento delle traiettorie attorno all'origine.

Il confine tra i casi considerati di un nodo e di una sella è il caso Quando uno degli indicatori caratteristici, per esempio λ 1 , svanisce, cosa che si verifica quando il determinante del sistema- espressione adbc=0(vedi formula 4.8 ). In questo caso, i coefficienti dei membri di destra delle equazioni (4.4) sono proporzionali tra loro:

e il sistema ha per stati di equilibrio tutti i punti della retta:

Le restanti curve integrali sono una famiglia di linee parallele con pendenza , lungo il quale i punti rappresentativi si avvicinano allo stato di equilibrio o se ne allontanano, a seconda del segno della radice seconda dell'equazione caratteristica λ 2 = a+d.(Fig.4.7 ) In questo caso le coordinate dello stato di equilibrio dipendono dal valore iniziale delle variabili.

Radici λ 1 , λ 2 – complessoconiugare

In questo caso, per davveroX E sì noi hanno coniugati complessi ξ , η (4.10) . Tuttavia, introducendo un'ulteriore trasformazione intermedia, è possibile anche in questo caso ridurre la considerazione ad una vera e propria trasformazione lineare omogenea. Mettiamo:

(4.16)

Dove un, b, E tu, v – valori reali. Si può dimostrare che la trasformazione dax,y A tu, v è, secondo le nostre ipotesi, reale, lineare, omogeneo con un determinante diverso da zero. A causa delle equazioni(4.10, 4.16) abbiamo:

Dove

(4.17)

Dividendo la seconda delle equazioni per la prima, noi abbiamo:

che è più facile da integrare, se passiamo al sistema di coordinate polari (R, φ ) . Dopo la sostituzione otteniamo da dove:

.(4.18)

Quindi, sul piano di fasetu, vabbiamo a che fare con una famiglia di spirali logaritmiche, ciascuna delle quali hapunto asintotico nell'origine.Punto singolare che è il punto asintotico di tutte le curve integrali a forma di spirale, amico annidato dentroamico, chiamato messa a fuoco ( fig.4.8 ) .

Consideriamo la natura del movimento del punto rappresentante lungo le traiettorie di fase. Moltiplicando la prima delle equazioni (4.17) pertu, e il secondo a v e aggiungendo , otteniamo:

Dove

Permettere UN 1 < 0 (UN 1 = Rifλ ) . Il punto rappresentante si avvicina quindi continuamente all'origine senza raggiungerla in un tempo finito. Ciò significa che le traiettorie di fase sono spirali tortuose e corrispondono a oscillazioni smorzate variabili. Questo - concentrazione costante .

Nel caso di un focus stabile, come nel caso di un nodo stabile, non è soddisfatta solo la condizione di Lyapunov, ma anche un requisito più severo. Vale a dire, per qualsiasi deviazione iniziale, il sistema alla fine ritornerà il più vicino possibile alla posizione di equilibrio. Viene chiamata tale stabilità, in cui le deviazioni iniziali non solo non aumentano, ma decadono, tendendo a zero stabilità assoluta .

Se nella formula (4.18) UN 1 >0 , allora il punto che rappresenta si allontana dall'origine, e abbiamo a che fare con messa a fuoco instabile . Quando ci si sposta da un aereotu, val piano di faseX, sìanche le spirali rimarranno spirali, ma saranno deformate.

Consideriamo ora il caso in cuiUN 1 =0 . Traiettorie di fase sul pianotu, vci saranno dei cerchi che sull'aereox,yadattare le ellissi:

Quindi, aun 1=0 attraverso un punto specialex= 0,y= 0 non passa alcuna curva integrale. Un tale punto singolare isolato, vicino al quale le curve integrali sono curve chiuse, in particolare ellissi incastrate l'una nell'altra e che racchiudono il punto singolare, è chiamato centro.

Sono quindi possibili sei tipi di equilibrio, a seconda della natura delle radici dell'equazione caratteristica (4.7). Vista delle traiettorie di fase sul piano x, y per questi sei casi è mostrato in Fig. 4.9.

Riso. 4.9.Tipi di ritratti di fase nell'intorno di uno stato stazionario per il sistema di equazioni lineari (4.4).

I cinque tipi di stati di equilibrio sono approssimativi, la loro natura non cambia con cambiamenti sufficientemente piccoli nei membri di destra delle equazioni (4.4). In questo caso, i cambiamenti dovrebbero essere piccoli non solo nei membri di destra, ma anche nelle loro derivate del primo ordine. Il sesto stato di equilibrio – il centro – non è grossolano. Con piccoli cambiamenti nei parametri del lato destro delle equazioni, entra in un focus stabile o instabile.

Diagramma di biforcazione

Introduciamo la notazione:

. (4.11)

Allora l’equazione caratteristica può essere scritta nella forma:

. (4.12)

Consideriamo un piano di coordinate cartesiane rettangolari S , D e segnare su di esso le aree corrispondenti all'uno o all'altro tipo di stato di equilibrio, che è determinato dalla natura delle radici dell'equazione caratteristica

.(4.13)

La condizione per la stabilità dello stato di equilibrio sarà la presenza di una parte reale negativa di yl 1 e l 2 . Condizione necessaria e sufficiente a tal fine è il soddisfacimento delle disuguaglianzeS > 0, D > 0 . Nel diagramma (4.15), questa condizione corrisponde ai punti situati nel primo quarto del piano dei parametri. Il punto singolare sarà il focus sel 1 e l 2 complesso. Questa condizione corrisponde a quei punti del piano per i quali , quelli. punti compresi tra due rami di una parabolaS 2 = 4 D. Punti del semiasse S = 0, D>0, corrispondono a stati di equilibrio di tipo centrale. Allo stesso modo,l 1 e l 2 - segni validi, ma diversi, ad es. un punto singolare sarà una sella se D<0, eccetera. Di conseguenza, otteniamo un diagramma di partizione del piano dei parametri S, D, in regioni corrispondenti a diversi tipi di stati di equilibrio.

Riso. 4.10. Diagramma di biforcazione

per il sistema di equazioni lineari 4.4

Se i coefficienti del sistema lineare a, b, c, d dipendono da alcuni parametri, quindi quando questo parametro viene modificato, cambieranno anche i valoriS , D . Quando si attraversano i confini, la natura del ritratto di fase cambia qualitativamente. Pertanto, tali confini sono chiamati confini di biforcazione: sui lati opposti del confine, il sistema ha due ritratti di fase topologicamente diversi e, di conseguenza, due diversi tipi di comportamento.

Il diagramma mostra come possono avvenire tali cambiamenti. Se escludiamo casi particolari - l'origine delle coordinate - allora è facile vedere che la sella può entrare in un nodo, stabile o instabile quando attraversa l'asse y. Un nodo stabile può spostarsi su una sella o su un focus stabile e così via. Si noti che le transizioni nodo stabile-fuoco stabile e nodo instabile-fuoco instabile non sono biforcative, poiché la topologia dello spazio delle fasi non cambia in questo caso. Parleremo più in dettaglio della topologia dello spazio delle fasi e delle transizioni di biforcazione nella Lezione 6.

Durante le transizioni di biforcazione, la natura della stabilità del punto singolare cambia. Ad esempio, una messa a fuoco stabile attraverso il centro può trasformarsi in una messa a fuoco instabile. Questa biforcazione si chiama Biforcazione Andronov-Hopf dai nomi degli scienziati che lo hanno studiato. Con questa biforcazione nei sistemi non lineari nasce un ciclo limite e il sistema diventa auto-oscillante (vedi lezione 8).

Esempio. Sistema di reazioni chimiche lineari

Sostanza X fluisce dall'esterno a velocità costante, si trasforma nella sostanza Y e ad una velocità proporzionale alla concentrazione della sostanza Y, viene tolto dalla sfera di reazione. Tutte le reazioni sono del primo ordine, ad eccezione dell'afflusso di materia dall'esterno, che è di ordine zero. Lo schema di reazione è il seguente:

(4.14)

ed è descritto dal sistema di equazioni:

(4.15)

Otteniamo concentrazioni stazionarie uguagliando i lati di destra a zero:

.(4.16)

Consideriamo il ritratto di fase del sistema. Dividiamo la seconda equazione del sistema (4.16) per la prima. Noi abbiamo:

.(4.17)

L'equazione (4.17) determina il comportamento delle variabili sul piano di fase. Costruiamo un ritratto di fase di questo sistema. Per prima cosa disegniamo le principali isocline sul piano delle fasi. Equazione dell'isoclina delle tangenti verticali:

Equazione per l'isoclina delle tangenti orizzontali:

Il punto singolare (stato stazionario) si trova all'intersezione delle principali isocline.

Determiniamo ora con quale angolo gli assi delle coordinate intersecano le curve integrali.

Se x= 0, quindi .

Pertanto, la tangente della pendenza della tangente alle curve integrali y=y(x), attraversando l'asse y x=0, è negativo nel semipiano superiore (ricordiamo che le variabili x, y hanno valori di concentrazione, e quindi a noi interessa solo il quadrante in alto a destra del piano di fase). In questo caso il valore della tangente dell'angolo di inclinazione della tangente aumenta con la distanza dall'origine.

Considera l'asse y= 0. All'intersezione di questo asse, le curve integrali sono descritte dall'equazione

A la tangente della pendenza delle curve integrali che attraversano l'asse delle ascisse è positiva e cresce da zero a infinito con l'aumentare X.

A .

Poi, con un ulteriore aumento, la tangente della pendenza diminuisce in valore assoluto, rimanendo negativa e tendendo a -1 X ® ¥ . Conoscendo la direzione delle tangenti alle curve integrali sulle principali isocline e sugli assi coordinati, è facile costruire l'intero quadro delle traiettorie di fase.

La natura della stabilità del punto singolare verrà stabilita utilizzando il metodo Lyapunov. Il determinante caratteristico del sistema ha la forma:

.

Espandendo il determinante, otteniamo l’equazione caratteristica del sistema: , cioè. le radici dell'equazione caratteristica sono entrambe negative. Pertanto, lo stato stazionario del sistema è un nodo stabile. Allo stesso tempo, la concentrazione della sostanza X tende ad uno stato stazionario sempre in modo monotono, la concentrazione della sostanza Y può passare da min a max. I regimi oscillatori in un tale sistema sono impossibili.

Permettere zq - punto singolare della funzione f(z), t.s. f(z) ma è analitico a questo punto (in particolare, potrebbe non essere definito a questo punto). Se esiste un intorno del punto così forato zq (cioè l'insieme O z - zq f(z) è quindi aliatico zo chiamato punto singolare isolato funzioni f(z). Questa definizione è conservata anche nel caso zn = oo, se lo iodio è un quartiere forato di un punto zq = oo comprendi l'insieme z > IO - l'apparizione di un cerchio centrato nell'origine. In altre parole, il punto singolare zq si dice isolato se esiste un intorno di questo punto in cui esistono altri punti singolari diversi da esso zq. Ovunque di seguito, consideriamo solo i punti singolari di un carattere a valore singolo (la funzione f(z) ritenuto unico).

A seconda del comportamento della funzione f(z) A z -> zq Esistono tre tipi di punti singolari. Punto singolare isolato funzioni zq f(z) chiamato:

1) punto singolare rimovibile se esiste un limite finito

2) palo se c'è un limite

3) punto essenziale, Se f(z) non ha né un limite finito né un limite infinito per z-> zq.

ESEMPIO 26.1. Mostriamo che tutti e tre i tipi di punti singolari sono realizzati. Prendere in considerazione F(z)= punto zq = 0 è isolato

punto singolare di questa funzione. Usando la formula (22.12), otteniamo l'espansione

da cui segue che esiste lim fi(z)= 1. Pertanto zq = 0 lo è

è un punto singolare rimovibile della funzione fi(z).

Funzione f'j(z) =--- ha un palo in un punto zo= 1 perché

2 R" X

Consideriamo ora la funzione )z(z)= e 1 ^ r e dimostralo zo = O è un punto singolare essenziale di questa funzione. Quando ti sforzi z a zero lungo l'asse reale, i limiti sinistro e destro della funzione f (z) diverso: lim Con 1 / 1 = 0,lim con 1 /* = os. Ciò implica,

x->0-0 x->0+O

Che cosa f:i(z) non ha né un limite finito né un limite infinito per 2 -> Oh, cioè zq = 0 è un punto singolare essenziale di questa funzione. (Nota che, come tende il punto z-iy a zero sulla funzione dell'asse immaginario

non ha alcun limite.)

Naturalmente esistono anche punti singolari non isolati. Per esempio. la funzione ha poli nei punti zn = -, P= ±1, ±2,...

Quindi, Zq = 0 è un punto singolare non isolato di questa funzione: in qualsiasi intorno (arbitrariamente piccolo) di questo punto ci sono altri punti singolari g pag.

Permettere zo- punto singolare isolato finale di una funzione f(z). Poi f(z)è simile in qualche quartiere perforato 0 Zo del punto zo questo intorno può essere considerato come un anello di raggio interno r = 0. Per il Teorema 25.1, nell'intorno in esame, la funzione f(z) può essere espanso in una serie di Laurent (25.2). Mostreremo che il comportamento della funzione per 2 -> zq (ovvero il tipo di punto singolare zo) dipende dalla forma della parte principale della scomposizione (25.2); questa circostanza spiega l'origine del termine “parte principale”.

TEOREMA 2G.2. Un punto singolare isolato zo di una funzione f(z) è rimovibile se e solo se l'espansione di Lorap in un intorno punteggiato di questo punto ha l'oid

quelli. consiste solo della parte corretta, e tutti i coefficienti della parte principale sono uguali al proiettile.

Prova. 1. Lascia zoè un punto singolare rimovibile. Dimostriamo che lo sviluppo di Laurent della funzione f(z) ha la forma (26.1). Dal punto singolare zo rimovibile, allora esiste un limite finito f(z) = A. Quindi, f(z) delimitato in qualche intorno forato 0 z - zq del punto zo, quelli. )(z) per tutti z da questo quartiere. Prendine uno qualsiasi R. U р /?|, e utilizzare le formule (25.3) per i coefficienti della serie di Laurent:

Per i coefficienti della parte principale dell'espansione n =- 1,-2,... Per tali valori P abbiamo p~n-e 0 a R-> 0. Poiché il valore R può essere scelto arbitrariamente piccolo, quindi Signor~" può essere arbitrariamente piccolo. Poiché |c t,| ^ Signor~n e cn non dipendono da p, allora cn = 0 per E= - 1, -2,..., che era da dimostrare.

2. Supponiamo ora che lo sviluppo di Laurent abbia la forma (26.1). La serie (26.1) è una serie di potenze e. converge quindi non solo nella zona forata, ma anche nell'intero quartiere z-zq compreso il punto zo; la sua somma S(z)è analitico per z e S(z) = )(z) a 0z - zo R. Pertanto esiste un limite finito )(z)\u003d Pm 5 (r) \u003d 5 (r) - Pertanto, il punto singolare zq

Z->Zo Z-*Zo

monouso. Il teorema è stato dimostrato.

Commento. Dalla dimostrazione del teorema segue che in un intorno perforato 0 z - zo di un punto singolare rimovibile, la funzione f(z) coincide con la funzione S(r), che è analitica nell'intero intorno z - zo. Pertanto, se poniamo /(th) = S(zq), quindi, senza modificare i valori della funzione f(z) in qualsiasi punto dell'intorno perforato, rendiamo questa funzione analitica in r, cioè "rimuovere" la funzione. Questo spiega il termine “singolarità rimovibile”. È naturale considerare tali punti come punti regolari e non come punti singolari della funzione f(z).

Consideriamo ad esempio la funzione

Nell’esempio 26.1 è stato dimostrato che Pm (n) = 1. cioè punto singolare

zq = 0 è rimovibile. Ponendo /i(0) = 1, eliminiamo così la singolarità e otteniamo una funzione analitica nel punto zq = 0 (e nell'intero piano C).

Caratterizziamo ora i poli in termini di espansioni di Laurent.

Teorema 26.3. Un punto singolare isolato Zo di una funzione f(z) è un polo se e solo se, quando la parte principale dello sviluppo di Laurent con centro Zq ha solo un numero finito di distinti

da zero coefficienti con n:

Prova. 1. Lascia zq - polo, cioè lim /( z) = oh.

Dimostriamo che lo sviluppo di Laurent della funzione f(z) ha la forma (2G.2). Dal lim f(z)= oh. allora esiste un intorno forato del punto

ki zq. in cui f(z)è analitico e non ha zeri. Quindi la funzione g(z) = 1 /f(z) sarà anche analitico in questo quartiere forato, e lim g(z)= 0. Pertanto, Zoè usa e getta *-? *0

punto singolare della funzione g(z). Ridefiniamo g(z) al punto zo, mettendo g(zo)= 0. Allora g(z) diventa analitico in tutto l'intorno del punto (non perforato). z0, E z0 sarà il suo zero isolato. Denotare con N molteplicità (ordine) di questo zero. Come è stato mostrato nel §23, in un intorno del punto funzione zq g(z) rappresentabile nella forma (vedi (23.2))

E (z$) f 0 e y>(z)è analitico in qualche intorno del punto zo- Perché ip(z) continuo nel punto zo E g>(zo) F 0" quindi ip(z) non ha zeri nemmeno in qualche intorno di questo punto. Quindi funzione 1 /-p(z) sarà analitico anche in questo intorno e, quindi, lo espande in una serie di Taylor:

Espandendo le parentesi e modificando le designazioni dei coefficienti, scriviamo l'ultima espansione nel modulo

dove c_jv = 1>o f 0. Pertanto, la parte principale dello sviluppo di Laurent di f(r) contiene solo un numero finito di termini; siamo arrivati ​​all'uguaglianza richiesta (26.2).

2. Inserisci un quartiere forato di un punto th funzione )(z)è rappresentato dallo sviluppo di Laurent (26.2) (in una forma più estesa, vedere (26.3)), la cui parte principale contiene solo un numero finito di termini, e Con- D" F 0. Dobbiamo dimostrarlo Zq - polo funzionale f(z). Moltiplicando l'uguaglianza (26.3) per (G - G o) iV , otteniamo la funzione

La serie in (26.4) è una serie di potenze che converge ad una funzione analitica non solo nel punto forato, ma anche nell'intero intorno del punto Zq. Pertanto, la funzione h(z) diventa analitico in questo quartiere se lo estendiamo in th ambientando h(zo)= s_dg F 0. Allora

Quindi il punto o è un polo, e il Teorema 26.3 è dimostrato.

Molteplicità (ordine) della funzione zero g(z)= 1//(r) viene chiamato ordine dei poli funzione /(r). Se N- l'ordine dei poli è quindi th g(z)= (r- Zo)N ip(z), e vai) F 0, e, come mostrato nella prima parte della dimostrazione del Teorema 26.3, lo sviluppo di f(r) ha la forma (26.3), dove c_/v F 0. Viceversa, se f(r) si espande nella serie (26.3) e ez F 0, allora

t.s. N- l'ordine del polo della funzione f(r). Così, l'ordine del polo zq della funzione/(G) è uguale al numero del coefficiente iniziale diverso da zero della parte principale dell'espansione di Laurent nell'intorno perforato del punto zq(cioè uguale a tale numero N, cosa s_dg F 0 e sp= 0 a P > N).

Dimostriamo la seguente affermazione, che è conveniente) per le applicazioni.

Corollario 26.4. Il punto zq è un polo di ordine N della finzione/(G) se e solo se/(G) rappresentare nella forma

dove h(z) è una funzione analitica in un intorno di un punto th e h(zo) f 0.

Prova. Funzione cp(z) = l/h(z)è analitico in qualche intorno del punto r. La condizione del Corollario 26.4 è equivalente alla seguente:

Ecco perché zq - molteplicità zero N funzioni g(z). e quindi il polo della molteplicità N funzioni /(2).

II esempio 26.5. Trovare i punti singolari isolati di una funzione e determinarne il tipo.

D e u c zio n I punti in cui (z 2 + 1 )(z+ H) 2 = 0. Se z 2 L- 1 = 0 quindi 2 = ±r Se (z 4- H) 2 = 0, allora z= -3. Pertanto la funzione ha tre punti singolari z= r, 22 = -r, Z3 = - 3. Considera z:

G - polo del primo ordine (abbiamo utilizzato il Corollario 26.4). Si può dimostrare in modo simile che 22 = -io anche un polo del primo ordine. Per 2h abbiamo:

Passiamo alla considerazione di punti essenzialmente singolari.

Teorema 26.6. Un punto singolare isolato zq di una funzione f(z) è essenzialmente singolare se e solo se la parte principale dello sviluppo di Laurent centrato in zq ha infiniti punti diversi da. zero, coefficienti con p.

Prova. Il Teorema 26.6 segue direttamente dai Teoremi 26.2 e 26.3. In effetti, se il punto zq è essenzialmente singolare, allora la parte principale dello sviluppo di Laurent non può essere assente o contenere un numero finito di termini (altrimenti il ​​punto Zq sarà rimovibile o a palo). Pertanto, il numero di termini nella parte principale deve essere infinito.

Al contrario, se la parte principale contiene infiniti membri, allora Zq non può essere né un punto rimovibile né un polo. Di conseguenza, questo punto è essenzialmente singolare.

Secondo la definizione, un punto essenzialmente singolare è caratterizzato dal fatto che la funzione f(2) non ha né limite finito né infinito per z ->zq. Un'idea più completa di quanto sia irregolare il comportamento di una funzione in un intorno di un punto essenzialmente singolare è data dal seguente teorema.

Teorema 26.7 (Teorema di Sochocki). Se zq è essenzialmente singolare, allora il punto della funzione f(z), quindi per qualsiasi numero complesso L, compreso A = oh, esiste una successione di punti z n tale che z n -> zo e lim f(zn) = UN.

n->os

Prova. Consideriamo innanzitutto il caso A = oh. Nella prima parte della dimostrazione del Teorema 2G.2, abbiamo stabilito che se f(z)è limitato in qualche intorno forato del punto r0, allora tutti i coefficienti c, n = - 1, - 2,... della parte principale sono uguali a zero (e, di conseguenza, la singolarità in th è asportabile). Poiché, per ipotesi, r è un punto essenzialmente singolare, la funzione /(r) è illimitata in qualsiasi intorno del punto r. Prendiamo un intorno stretto 0 Z tale che f(zi) > 1 (se |/(r)| z - zo R/2 c'è un punto z-2 , dove |/(dd)| > 2, ecc.: nel quartiere forato O 71. È ovvio che rn -e go e lim /(r«) = oo. Quindi, nel caso A = oo, Teorema 26.7

provato.

Andiamo adesso Af oh. Supponiamo innanzitutto che esista un intorno 0 perforato

= -aa---- sarà analitico in questo quartiere forato e, di conseguenza,

/(G) - UN

di conseguenza, r è un punto singolare isolato della funzione Φ(r). Mostriamo. che r0 è un punto essenzialmente singolare di Φ(r). Lascia che sia sbagliato. Allora esiste un limite lim Φ(r), finito o infinito. Perché

/(r) = A + , allora esiste anche Hsh /(r), il che contraddice la condizione

F(g) ~ :-*z0

vista del teorema. Quindi r0 è un punto essenzialmente singolare della funzione Φ(r). Secondo quanto dimostrato sopra, esiste una successione di punti r n tale che r n o e lim Φ(r n) = oo. Da qui

Abbiamo dimostrato l’asserzione richiesta assumendo che f(r) FA in qualche intorno forato del punto r. Supponiamo ora che questo non sia vero, cioè in ogni intorno forato arbitrariamente piccolo del punto th c'è un tale punto G", che f(r") = A. Allora per qualsiasi P nell'intorno perforato 0 f(z u) = L. Pertanto, l'asserzione richiesta è vera P-Yuo

in tutti i casi, e il Teorema 26.7 è dimostrato.

Secondo il Teorema 26.7 (di Sokhotsky), in qualsiasi intorno forato (arbitrariamente piccolo) di un punto essenzialmente singolare, la funzione f(r) assume valori arbitrariamente vicini a qualsiasi numero nel piano complesso esteso C.

Per studiare i punti singolari isolati sono spesso utili i noti sviluppi di Taylor delle funzioni elementari di base.

ESEMPIO 2G.8. Determina il tipo di punto singolare zq = 0 per la funzione

Risolto ed e. Espandiamo il numeratore e il denominatore in una serie di Taylor in potenze di r. Sostituendo nella (22.11) 3 z invece di r e sottraendo 1, otteniamo

Utilizzando la (22.12), otteniamo l'espansione del denominatore:

Le serie in questi sviluppi convergono nell'intero piano complesso €. Abbiamo

e /2(2) sono analoghi in un intorno del punto zo = 0 (e anche nell'intero piano) e /2(20) F 0, allora h(z)è anche analitico in qualche intorno del punto gF 0. Secondo il Corollario 26.4, il punto Zo = 0 è il polo dell'ordine N = 4.

II esempio 26.9. Trovare i punti singolari di una funzione f(z)= sin j - e determinarne il tipo.

P e in e ed e. La funzione ha un unico punto singolare finale zq = 1. In altri punti da C, la funzione w =--- analitico; da qui la funzione peccato w sarà analitico.

Sostituendo nell'espansione del seno (22.12) - invece di r, otteniamo

Abbiamo ottenuto l'espansione della funzione sin in una serie di Laurent in un intorno forato del punto 20 = 1. Poiché l'espansione risultante contiene infiniti termini con potenze negative (r - 1), allora zq = 1 è un punto singolare essenziale (in questo caso lo sviluppo di Laurent è costituito solo dalla parte principale e la parte corretta è assente).

Si noti che anche in questo caso è stato possibile stabilire la natura della singolarità direttamente dalla definizione, senza ricorrere allo sviluppo in serie. In effetti, ci sono sequenze (r") e (2") che convergono zo= 1, e così via f(z"n)= 1, /(2") = 0 (specifica tu stesso tali sequenze). Quindi, f(z) non ha limiti quando z -> 1 e da qui il punto zq - 1 è essenzialmente singolare.

Introduciamo il concetto di sviluppo di Laurent di una funzione in un intorno di un punto Zq = 00 e consideriamo a questo punto la connessione tra l'espansione e la natura della singolarità. Si noti che le definizioni di punto singolare isolato e il suo tipo (rimovibile, polare o essenzialmente singolare) si applicano al caso zq = oc invariato. Ma i Teoremi 26.2. 26.3 e 26.6, relativi alla natura delle espansioni Laurent, devono essere modificati. Il punto è che i membri cn (z- 2o) pag. P= -1,-2,..., la parte principale, che definisce l'"irregolarità" della funzione vicino al punto finale Zq, poiché 2 tende a oo, si comporteranno “correttamente” (tenderanno a 0). Al contrario, i membri della parte regolare con P= 1,2,... tenderà a oo; determinano la natura della singolarità in Zq = oo. Pertanto, la parte principale dell'espansione nell'intorno di oo saranno i termini con potenze positive P, e corretto - con negativo.

Introduciamo una nuova variabile w = 12. Funzione tv= 1/2, esteso in modo che u(oo) = 0, uno a uno e mappa in modo conforme l'intorno z > R punti zq = 00 nell'intorno di |w| wq = 0. Se la funzione f(z) analisi in un quartiere perforato R z Zq = oc, quindi la funzione G(l) = f(l/l) sarà analitico nell'intorno giallo 0 wo = 0. Poiché per 2 -> oo ci sarà w-> 0, quindi

Ecco perché Sol(w) ha al punto wq = 0 è una singolarità dello stesso tipo di f(z) al punto Zq = 00. Espandiamo la funzione G(w) in una serie di Laurent in un intorno perforato del punto wo = 0:

Le somme sul lato destro della (26.5) rappresentano rispettivamente la parte corretta e quella principale dell'espansione. Passiamo alla variabile z, sostituendo w = 1/z:

denotando P\u003d -A *, 6 * \u003d 6_ " \u003d con pag e notandolo G(l/z) = f(z), noi abbiamo

La scomposizione (2G.G) viene chiamata Espansione di Laurent della funzione f(z) in un intorno perforato del punto zq= oh. Viene chiamata la prima somma in (2G.6). parte destra, e la seconda somma è parte principale questa decomposizione. Poiché queste somme corrispondono alla parte corretta e principale dell'espansione (26.5), l'espansione (26.6) soddisfa gli analoghi dei Teoremi 26.2, 26.3 e 26.6. Pertanto, il seguente teorema è un analogo del Teorema 26.2.

Teorema 26.10. Punto singolare isolatoZq - os (funzioni/(G) è rimovibile se e solo se l'espansione di Laurent in un intorno forato di questo punto ha la forma

t.s. consiste solo della parte corretta.

Mettiamo /(oo) = co. La funzione definita dalla serie (26.7) converge nell'intorno z > R punti 2o \u003d oc, chiamati analitico al punto z o = oo. (Si noti che questa definizione equivale all'analiticità della funzione G(w) al punto wo = 0.)

Esempio 26.11. Investigare il punto singolare zq = oo della funzione

Poiché il limite è finito, allora zo = oo è un punto singolare rimovibile della funzione f(r). Se mettiamo /(oo) = lim J(z)= 0, quindi f(z) diventerà

tic al punto Zo= os. Mostriamo come trovare lo sviluppo corrispondente (26.7). Passiamo alla variabile w = 1 fz. Sostituendo z= 1 /?e, otteniamo

(l'ultima uguaglianza è valida nell'intorno punteggiato del punto w0 = 0, ma estenderemo la definizione (7(0) = 0). La funzione risultante ha punti singolari w =±i, w =-1/3, e al punto Wq = 0 è analitico. Funzione espandibile Sol(w) per gradi w(come è stato fatto nell'Esempio 25.7) e sostituendo nella serie di potenze risultante w = 1/z si può ottenere lo sviluppo (26.7) della funzione f(z).

Teorema 26.3 per il caso zo= oo verrà riscritto nella forma seguente.

Teorema 26.12. Punto singolare isolato vai = os la funzione f(z) è un polo se e solo se è la parte principale dello sviluppo di Laurent (26.6) ha solo un numero finito di coefficienti diversi da zero Con":

Qui la serie è la parte regolare e il polinomio tra parentesi è la parte principale dello sviluppo. La molteplicità del polo in oc è definita come molteplicità del polo wq = 0 funzioni G(z).È facile vedere che la molteplicità del polo coincide con il numero N nella (26.8).

Q p | (i2+1) (z+3)2

Compito. Mostra che la funzione f(z) =-- -- ha dentro

punto zo = oo ordine dei poli 3.

Il Teorema 26.6 su un punto essenziale singolare viene riscritto per il caso in esame zo= os quasi testualmente, e non ci soffermiamo su di esso in dettaglio.

Concetti e definizioni di base:

Lo zero della funzione analitica f(z) è il punto “a” per il quale f(a)=0.

Lo zero di ordine “n” della funzione f(z) è il punto “a” se ma fn(a)¹0.

Un punto singolare "a" è detto punto singolare isolato della funzione f(z) se esiste un intorno di questo punto dove non ci sono punti singolari diversi da "a".

I punti singolari isolati sono di tre tipi: .

1 punto speciale removibile;

3 punti singolari essenziali.

Il tipo di un punto singolare può essere determinato in base al comportamento della funzione data nel punto singolare trovato, nonché dalla forma della serie di Laurent ottenuta per la funzione nell'intorno del punto singolare trovato.

Determinare il tipo di un punto singolare in base al comportamento della funzione in esso.

1. Punti singolari rimovibili.

Un punto singolare isolato a della funzione f(z) si dice rimovibile se esiste un limite finito .

2. Poli.

Un punto singolare isolato a della funzione f(z) è detto polo se .

3. Punti singolari significativi.

Un punto singolare isolato a di una funzione f(z) è detto punto singolare essenziale se non esiste né finito né infinito.

Tra gli zeri e i poli della funzione ha luogo la seguente relazione.

Affinché un punto a sia un polo di ordine n della funzione f(Z), è necessario e sufficiente che questo punto sia uno zero di ordine n per la funzione .

Se n=1 il polo si dice semplice.

Definizione: Un punto singolare isolato di un carattere a valore singolo è chiamato:

a) rimovibile se la parte principale della decomposizione è assente;

b) un palo se la parte principale contiene un numero finito di membri;

c) un punto essenzialmente singolare se la parte principale contiene un numero infinito di termini.

a) Pertanto, in un intorno di un punto singolare rimovibile, l'espansione ha la forma:

esprime la funzione in tutti i punti della circonferenza |z-a|

Al centro z=a l'uguaglianza è falsa, perché la funzione in z=a ha una discontinuità e il lato destro è continuo. Se si modifica il valore della funzione al centro, portandolo uguale al valore del lato destro, allora lo scarto eliminato – da qui il nome – sarà eliminabile.

b) In un intorno di un polo di ordine m, lo sviluppo in serie di Laurent ha la forma:

c) In prossimità di un palo semplice

Detrazioni e formule per il loro calcolo.

Il residuo di una funzione analitica f(z) in un punto singolare isolato z 0 è un numero complesso uguale al valore dell'integrale , preso in direzione positiva lungo il cerchio L centrato nel punto z 0 , che giace nella regione di analiticità della funzione f(z) (cioè nell'anello 0<|z-z0|

Il residuo della funzione f(z) in un punto singolare isolato z 0 è indicato con il simbolo Res f(z 0) o Res (f(z); z 0). Così,

Rif(z0)= . (22.15.1)

Se inseriamo n=-1 nella formula (22.15.1), otteniamo:

C-1=

oppure Res f(z 0)= C -1 ,

quelli. il residuo della funzione f(z) rispetto al punto singolare z 0 è pari al coefficiente del primo termine con esponente negativo nello sviluppo della funzione f(z) in una serie di Laurent.

Calcolo delle detrazioni.

Punti singolari regolari o rimovibili. Ovviamente, se z=z 0 è un punto singolare regolare o rimovibile della funzione f(z), allora Res f(z 0)=0 (non esiste una parte principale nella scomposizione di Laurent in questi casi, quindi c-1= 0).

Polo. Sia il punto z 0 un polo semplice della funzione f(z). Allora la serie di Laurent per la funzione f(z) in un intorno del punto z 0 ha la forma:

Da qui

Pertanto, passando questa uguaglianza al limite come z --z 0 , otteniamo

Risf(z0)=

Punto essenzialmente speciale. Se il punto z 0 è un punto essenzialmente singolare della funzione f(z), allora per calcolare il residuo della funzione in questo punto, di solito si determina direttamente il coefficiente c-1 nello sviluppo della funzione in una serie di Laurent.

Classificazione degli eventi. Somma, prodotto di eventi, loro proprietà, rappresentazione grafica.

Gli eventi si dividono in:

1. Casuale

2. Credibile

3. Impossibile

Affidabile: questo è un evento che si verifica necessariamente in queste condizioni (la notte è seguita dal mattino).

Il casuale è un evento che può verificarsi o meno (il superamento di un esame).

L'impossibile è un evento che non si verificherà nelle condizioni date (prendi una matita verde dalla scatola con solo quelle rosse).

punto singolare

in matematica.

1) Punto singolare della curva dato dall'equazione F ( x, y) = 0, - punto M 0 ( x0,y0), in cui entrambe le derivate parziali della funzione F ( x, y) svaniscono:

Se, inoltre, non tutte le derivate parziali seconde della funzione F ( x, y) nel punto M 0 sono uguali a zero, allora O. t. si dice doppio. Se con lo svanire delle derivate prime nel punto M 0 si annullano tutte le derivate seconde, ma non tutte le derivate terze sono uguali a zero, allora l'O.t. si dice triplo, e così via. Quando si studia la struttura di una curva vicino ad una doppia O. t., un ruolo importante è giocato dal segno dell'espressione

Se Δ > 0 allora l'O.t. si dice isolato; ad esempio, la curva y 2 - x 4 + 4x 2= 0 l'origine è un O. t. isolato (vedi riso. 1 ). Se Δ x 2 + y 2 + a 2) 2 - 4a2x2-a4= 0 l'origine delle coordinate è il nodale O. t. (vedi riso. 2 ). Se Δ = 0, allora la curva O. t. è isolata o caratterizzata dal fatto che diversi rami della curva hanno una tangente comune in questo punto, ad esempio: tangente e formano un punto, come una curva y 2 - x 3= 0 (vedi riso. 3 , UN); b) cuspide di 2° tipo - diversi rami della curva si trovano sullo stesso lato della tangente comune, come una curva (y-x2)2-x5= 0 (vedi riso. 3 , B); c) punto di autocontatto (per una curva y 2 - x 4= 0 l'origine è un punto di autocontatto; (cm. riso. 3 , V). Insieme all'O.t. specificato ci sono molti altri O.t. con nomi speciali; ad esempio, un punto asintotico è l'apice di una spirale con un numero infinito di giri (vedi Fig. riso. 4 ), punto di interruzione, punto d'angolo, ecc.

2) Un punto singolare di un'equazione differenziale è un punto in cui sia il numeratore che il denominatore del lato destro dell'equazione differenziale svaniscono simultaneamente (Vedi Equazioni differenziali)

dove P e Q sono funzioni continuamente differenziabili. Supponendo che O.t. sia situato all'origine delle coordinate e utilizzando la formula di Taylor (Vedi formula di Taylor), possiamo rappresentare l'equazione (1) nella forma

dove P1 ( x, y) e Q1 ( x, y) sono infinitesimali rispetto a

Vale a dire, se λ 1 ≠ λ 2 e λ 1 λ 2 > 0 oppure λ 1 = λ 2, allora O. t. è un nodo; in esso entrano tutte le curve integrali che passano per punti di un intorno sufficientemente piccolo del nodo. Se λ 1 ≠ λ 2 e λ 1 λ 2 i β, α ≠ 0 e β ≠ 0, allora O. t. è un fuoco; tutte le curve integrali che passano per punti in un intorno sufficientemente piccolo del fuoco sono spirali con un numero infinito di spire in qualsiasi intorno arbitrariamente piccolo del fuoco. Se infine λ 1,2 = ± ioβ, β ≠ 0, allora il carattere di O. t. non è determinato da termini lineari negli sviluppi di P ( x, y) e Q ( x, y), come è avvenuto in tutti i casi sopra menzionati; qui O. t. può essere un focus o un centro, oppure può avere un carattere più complesso. In prossimità del centro tutte le curve integrali sono chiuse e contengono al loro interno il centro. Quindi, ad esempio, il punto (0, 0) è un nodo per le equazioni A" = 2u/x(λ 1 = 1, λ 2 = 2; cfr riso. 5 , a) e sì" = u/x(λ 1 = λ 2 = 1; cfr riso. 5 , b), una sella per l'equazione y" = -y/x(λ 1 = -1, λ 2 = 1 ; cm. riso. 6 ), il focus dell'equazione y" =(x + y) / (x-y) (λ1 = 1 - io, λ2 = 1 + io; cm. riso. 7 ) e il centro dell'equazione y" = -x / y(λ1 = -io, λ2 = io; cm. riso. 8 ).

Se x, y) e Q ( x, y) sono analitici, l'intorno di un O. t. di ordine superiore può essere diviso in regioni: D 1 - riempito con curve integrali, entrambe le estremità entrano nell'O. t. (regioni ellittiche), D 2 - riempito con curve integrali, un'estremità che entra nell'O. t. (regioni paraboliche), e D 3 - regioni delimitate da due curve integrali incluse nell'O. t., tra le quali vi sono curve integrali del tipo di iperboli (regioni iperboliche) (vedi. riso. 9 ). Se non ci sono curve integrali che entrano in un punto O., allora il punto O. è chiamato punto di tipo stabile. L'intorno di un O. t. stabile è costituito da curve integrali chiuse contenenti O. t. al loro interno, tra le quali si trovano le spirali (vedi Fig. riso. 10 ).

Lo studio delle equazioni differenziali di O. t., cioè, in sostanza, lo studio del comportamento delle famiglie di curve integrali in un intorno di O. t. M. Lyapunov a, A. Poincaré e altri).

3) Un punto singolare di una funzione analitica a valore singolo è un punto in cui l'analiticità della funzione viene violata (vedi Funzioni analitiche). Se c'è un quartiere di O. t. UN, libero da altri O. t., allora il punto UNè detto isolato O.t.If UNè un OT isolato ed esiste un OT finito è detto OT rimovibile. Modificando opportunamente la definizione della funzione nel punto a (o ridefinendola a questo punto, se la funzione non è affatto definita in esso), ovvero impostando F(UN)= b, è possibile raggiungere UN diventerà un punto ordinario della funzione corretta. Ad esempio, punto z= 0 è un OT rimovibile per la funzione f 1 ( z) = F(z), Se z≠ 0 e F 1(0),=1, punto z= 0 è un punto ordinario [ F 1 (z) è analitico in questo senso z= 0]. Se UN- isolato O. t. e a è detto polo o punto inessenzialmente singolare della funzione F(z), se la serie di Laurent) funziona F(z) in un quartiere di un O. t. isolato non contiene poteri negativi z-a, Se UN- O.t. rimovibile, contiene un numero finito di poteri negativi z-a, Se UN- polo (in questo caso, l'ordine del polo Rè definito come la potenza più alta di a - un punto essenzialmente singolare. Ad esempio, per la funzione

p = 2, 3, …)

punto z= 0 è il polo dell'ordine R, per la funzione

punto z= 0 è un punto singolare essenziale.

Sul confine del cerchio di convergenza di una serie di potenze deve esserci almeno una O.t. della funzione rappresentata all'interno di questo cerchio dalla serie di potenze data. Tutti i punti di confine del dominio di esistenza di una funzione analitica a valore singolo (confine naturale) sono punti di confine di questa funzione. Pertanto, tutti i punti della circonferenza unitaria | z| = 1 sono speciali per la funzione

Per una funzione analitica multivalore, il concetto di "O. T." più difficile. Oltre all'O. t., nei singoli fogli della superficie di Riemann di una funzione (ovvero l'O. t. degli elementi analitici a valore singolo), qualsiasi punto di diramazione è anche un O. t. della funzione. I punti di diramazione isolati di una superficie di Riemann (cioè punti di diramazione tali che in alcuni dei loro dintorni non ci sono altre funzioni O.t. in nessuna foglia) sono classificati come segue. Se a è un punto di diramazione isolato di ordine finito ed esiste un a finito, è chiamato polo critico. Se UNè un punto di diramazione isolato di ordine infinito e a è chiamato O trascendentale. Tutti gli altri punti di diramazione isolati sono chiamati punti critici essenzialmente singolari. Esempi: punto z= 0 è un punto critico ordinario della funzione f ( z) = logaritmo z e un punto singolare essenziale critico della funzione F (z) = log del peccato z.

Qualsiasi O.t., tranne quello rimovibile, è un ostacolo alla continuazione analitica, cioè la continuazione analitica lungo una curva che passa per un O.t. inamovibile è impossibile.

Grande Enciclopedia Sovietica. - M.: Enciclopedia sovietica. 1969-1978 .

Scopri cos'è "Punto speciale" in altri dizionari:

Punti qui. Vedi anche punto singolare (equazioni differenziali). Una caratteristica o singolarità in matematica è un punto in cui un oggetto matematico (di solito una funzione) non è definito o ha un comportamento irregolare (ad esempio, un punto in cui ... ... Wikipedia

Una funzione analitica è un punto in cui le condizioni dell’analiticità vengono violate. Se una funzione analitica f(z) è definita in qualche intorno del punto z0 ovunque... Enciclopedia fisica

Una funzione analitica è un punto in cui l'analiticità di una funzione viene violata... Grande dizionario enciclopedico

punto singolare- — [Ya.N. Luginsky, M.S. Fezi Zhilinskaya, Yu.S. Kabirov. Dizionario inglese russo di ingegneria elettrica e industria energetica, Mosca, 1999] Argomenti di ingegneria elettrica, concetti di base EN punto singolare ... Manuale del traduttore tecnico

1) Un OT di una funzione analitica f(z) è un ostacolo alla continuazione analitica di un elemento della funzione f(z) di una variabile complessa z lungo un percorso sul piano di questa variabile. Sia definita la funzione analitica f(z) da alcuni... ... Enciclopedia matematica

Una funzione analitica, il punto in cui l'analiticità della funzione viene violata. * * * PUNTO SINGOLARE PUNTO SINGOLARE di una funzione analitica, punto in cui l'analiticità della funzione è violata... Dizionario enciclopedico

punto singolare- ypatingasis taškas statusas T sritis automatika atikmenys: engl. punto singolare vok. singolare Punkt, m rus. punto singolare, fpranc. particella puntiforme, m; point singulier, m … Automatikos terminų žodynas

punto singolare- ypatingasis taškas statusas T sritis fizika atitikmenys: engl. punto singolare vok. singolare Punkt, m rus. punto singolare, fpranc. point singulier, m … Fizikos terminų žodynas

Le serie di Taylor servono come strumento efficace per studiare le funzioni analitiche nel cerchio zol Per studiare le funzioni analitiche in una regione anulare, risulta che è possibile costruire espansioni in potenze positive e negative (z - zq) della forma che generalizza gli sviluppi di Taylor. La serie (1), intesa come somma di due serie, è detta serie di Laurent. È chiaro che la regione di convergenza della serie (1) è la parte comune delle regioni di convergenza di ciascuna delle serie (2). Troviamola. L'area di convergenza della prima serie è un cerchio il cui raggio è determinato dalla formula di Cauchy-Hadamard All'interno del cerchio di convergenza, la serie (3) converge ad una funzione analitica e in qualsiasi cerchio di raggio minore converge assolutamente e uniformemente. La seconda serie è una serie di potenze rispetto alla variabile. La serie (5) converge nel suo cerchio di convergenza ad una funzione analitica della variabile complessa m - * oo, e in ogni cerchio di raggio minore converge assolutamente e uniformemente, il che significa che la regione di convergenza della serie (4) è l'apparenza del cerchio - Se quindi esiste una regione comune di convergenza delle serie (3) e (4) - un anello circolare in cui la serie (1) converge a una funzione analitica. Inoltre, in qualsiasi anello, converge in modo assoluto e uniforme. Esempio 1. Determinare la regione di convergenza della serie di Rad Laurent I punti singolari isolati e la loro classificazione (z), che è a valore singolo e apolitica in un anello circolare, possono essere rappresentati in questo anello come la somma di una serie convergente i cui coefficienti Cn sono determinati e calcolati in modo univoco dalle formule dove 7p è un cerchio di raggio m Fissiamo un punto arbitrario z all'interno dell'anello R Costruiamo cerchi con centro nel punto r i cui raggi soddisfano le disuguaglianze e consideriamo un nuovo anello.Secondo il teorema dell'integrale di Cauchy per un dominio molte volte connesso, abbiamo Trasformiamo ciascuno degli integrali nella somma (8) separatamente. Per tutti i punti £ lungo il cerchio 7d* è soddisfatta la relazione de la somma di una serie uniformemente convergente 1 1. Pertanto, la frazione ^ può essere rappresentata in vi- /" / In modo leggermente diverso, per tutti i punti ξ su il cerchio ir> abbiamo la seguente relazione Pertanto, la frazione ^ può essere rappresentata come la somma di una serie uniformemente convergente nelle formule (10) e (12) sono funzioni analitiche in un anello circolare. Pertanto, per il teorema di Cauchy, i valori degli integrali corrispondenti non cambiano se i cerchi 7/r e 7r/ vengono sostituiti da un cerchio qualsiasi. Questo ci permette di combinare le formule (10) e (12). Sostituendo gli integrali a destra della formula (8) con le loro espressioni (9) e (11), rispettivamente, otteniamo l'espansione desiderata. Poiché z è un arbitrario punto dell'anello, ne consegue che la serie ( 14) converge alla funzione f(z) ovunque in questo anello, e in ogni anello la serie converge a questa funzione in modo assoluto e uniforme. Proviamo ora che la scomposizione della forma (6) è unica. Supponendo che avvenga un'altra scomposizione, allora, ovunque all'interno dell'anello R, abbiamo Sulla circonferenza, le serie (15) convergono uniformemente. Moltiplica entrambi i lati dell'uguaglianza (dove m è un numero intero fisso e integra entrambe le serie termine per termine. Di conseguenza, otteniamo sul lato sinistro e sul lato destro - Csh. Pertanto, (4, \u003d St. Poiché m è un numero arbitrario, l'ultima serie di uguaglianza (6), i cui coefficienti sono calcolati dalle formule (7), è chiamata serie di Laurent della funzione f(z) nell'anello 7) per i coefficienti della serie di Laurent sono usati raramente nella pratica, perché, di regola, richiedono calcoli complicati. Di solito, se possibile, vengono utilizzate espansioni di Taylor già pronte di funzioni elementari. Sulla base dell'unicità dell'espansione, qualsiasi metodo legittimo porta allo stesso risultato. Esempio 2 Consideriamo gli espansioni in serie di Laurent di funzioni in domini diversi, assumendo che Fuiscius /(r) abbia due punti singolari: Pertanto, ci sono tre domini anulari, centrati nel punto r = 0. In ognuno dei quali la funzione /(r) è analitico: a) cerchio anello l'aspetto del cerchio (Fig. 27). Troviamo gli sviluppi di Laurent della funzione /(z) in ciascuna di queste regioni. Rappresentiamo /(z) come somma di frazioni elementari a) Relazione di trasformazione del cerchio (16) come segue Utilizzando la formula per la somma dei termini di una progressione geometrica, otteniamo b) L'anello per la funzione -z rimane convergente in questo anello, poiché la Serie (19) per la funzione j^j per |z| > 1 diverge. Trasformiamo quindi la funzione /(z) come segue: applicando nuovamente la formula (19), otteniamo che Questa serie converge per. Sostituendo gli sviluppi (18) e (21) nella relazione (20), otteniamo c) L'esteriorità del cerchio per la funzione -z con |z| > 2 divergenti e serie (21) per la funzione Rappresentiamo la funzione /(z) nella seguente forma: /<*>Utilizzando le formule (18) e (19), otteniamo OR 1. Questo esempio mostra che per la stessa funzione f(z) l'espansione di Laurent, in generale, ha diverso tipo per anelli diversi. Esempio 3. Trovare la scomposizione delle 8 serie di Laurent della funzione Serie di Laurent Punti singolari isolati e loro classificazione nella regione anulare A Usiamo la rappresentazione della funzione f (z) nella seguente forma: e trasformiamo il secondo termine Usando la formula per la somma dei termini di una progressione geometrica, otteniamo Sostituendo le espressioni trovate nella formula (22), abbiamo Esempio 4. Espandi la funzione in una serie di Laurent nell'intorno di zq = 0 sottile. Per qualsiasi complessa , abbiamo Sia che questa espansione sia valida per qualsiasi punto z Ф 0. In questo caso, la regione anulare è l'intero piano complesso con un punto z eliminato - 0. Questa regione può essere definita dalla seguente relazione: Questa funzione è analitica nella regione Dalle formule (13) per i coefficienti della serie di Laurent, con lo stesso ragionamento del paragrafo precedente, si ottengono le disuguaglianze di Kouiw. se la funzione f(z) è limitata su una circonferenza, dove M è una costante), allora punti singolari isolati Un punto zo è detto punto singolare isolato della funzione f(z) se esiste un intorno anulare del punto ( questo insieme è talvolta chiamato anche intorno forato del punto 2o), in cui la funzione f(z) è a valore singolo e analitica. Nel punto zo stesso, la funzione non è definita o non è a valore singolo e analitica. Si distinguono tre tipi di punti singolari a seconda del comportamento della funzione /(z) quando si avvicina al punto zo. Un punto singolare isolato si dice: 1) rimovibile se esiste un finito 2) pmusach se 3) punto essenzialmente singolare se la funzione f(z) non ha limite per Teorema 16. Un punto singolare isolato z0 di una funzione f(z) è un punto singolare rimovibile se e solo se lo sviluppo di Laurent della funzione f(z) in un intorno del punto zo non contiene una parte principale, cioè, ha la forma Let zo - punto singolare rimovibile. Allora ne esiste uno finito, e quindi la funzione f(z) è limitata in un intorno procologico del punto r. Poniamo In virtù delle disuguaglianze di Cauchy Poiché è possibile scegliere p come arbitrariamente piccolo, allora tutti i coefficienti sono negativi le potenze (z - 20) sono pari a zero: Viceversa, sia di Laurent lo sviluppo della funzione /(r) in un intorno del punto zq contenga solo la parte corretta, cioè abbia la forma (23) e, quindi , è Taylor. È facile vedere che per z -* z0 la funzione /(r) ha un valore limite: Teorema 17. Un punto singolare isolato zq della funzione f(z) è rimovibile se e solo se la funzione J(z) è delimitato in qualche intorno forato del punto zq, Zgmechai no. Sia r0 un punto singolare rimovibile di f(r). Supponendo di ottenere che la funzione f(r) sia analitica in una circonferenza centrata nel punto th. Questo definisce il nome del punto: usa e getta. Teorema 18. Un punto singolare isolato zq di una funzione f(z) è un polo se e solo se la parte principale dello sviluppo di Laurent della funzione f(z) in un intorno del punto contiene un numero finito (e positivo) di termini diversi da zero, cioè ha la forma 4 Sia z0 un polo. Da allora esiste un intorno forato del punto z0 in cui la funzione f(z) è analitica e diversa da zero. Allora una funzione analitica è definita in questo intorno, e quindi il punto zq è un punto singolare rimovibile (zero) della funzione o dove h(z) è una funzione analitica, h(z0) ∩ 0. è analitica in un intorno del punto zq, e quindi da dove otteniamo che. Supponiamo ora che la funzione f(z) abbia una scomposizione della forma (24) in un intorno forato del punto zo. Ciò significa che in questo intorno la funzione f(z) è analitica insieme alla funzione. Per la funzione g(z), vale l'espansione dalla quale risulta chiaro che zq è un punto singolare rimovibile della funzione g(z) ed esiste Allora la funzione tende a 0 - il polo della funzione Ce n'è un'altra semplice fatto. Il punto Zq è un polo della funzione f(z) se e solo se la funzione g(z) = y può essere estesa a una funzione analitica in un intorno del punto zq ponendo g(z0) = 0. L'ordine del polo della funzione f(z) è detto ordine zero della funzione jfa. I Teoremi 16 e 18 implicano la seguente affermazione. Teorema 19. Un sottile singolare isolato è essenzialmente singolare se e solo se la parte principale dello sviluppo di Laurent in un intorno punteggiato di questo punto contiene infiniti termini diversi da zero. Esempio 5. Il punto singolare della funzione è zo = 0. Abbiamo i punti singolari isolati della serie Laurent e la loro classificazione Pertanto, zo = 0 è un punto singolare rimovibile. Lo sviluppo della funzione /(z) in una serie di Laurent in prossimità del punto zero contiene solo la parte corretta: Esempio7. f(z) = Il punto singolare della funzione f(z) è zq = 0. Consideriamo il comportamento di questa funzione sugli assi reale e immaginario: sull'asse reale in x 0, sull'asse immaginario Pertanto, né finito né il limite infinito f(z) in z -* 0 non esiste. Quindi il punto r0 = 0 è un punto essenzialmente singolare della funzione f(z). Troviamo lo sviluppo di Laurent della funzione f(z) in un intorno del punto zero. Per ogni complesso C che abbiamo, impostiamo. Allora lo sviluppo di Laurent contiene un numero infinito di termini con potenze negative di z.