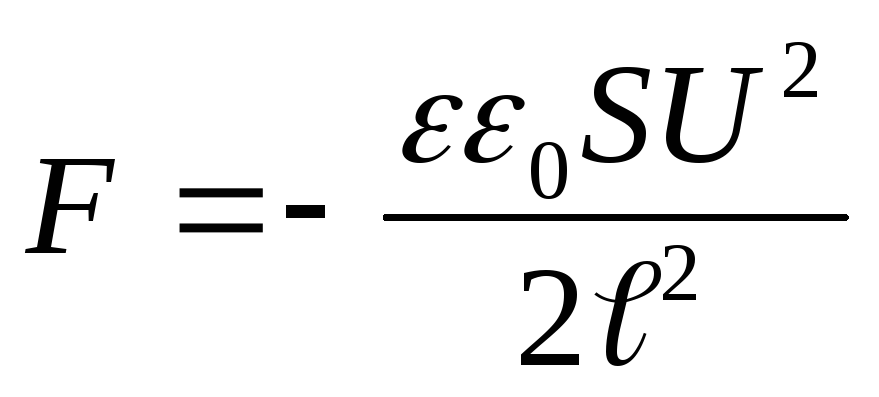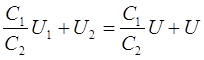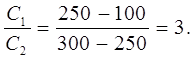Total potensialforskjell U 0 mellom elektrodene er
Beregninger:
Svar: overflateladningstetthet på platene til en kondensator
Oppgave 23
Plateareal flatt luftkondensator, avstanden mellom dem d=5 mm. En potensiell forskjell påføres platene til en kondensator. Etter at kondensatoren er koblet fra spenningskilden, er rommet mellom kondensatorplatene fylt med ebonitt. Hva blir potensialforskjellen mellom platene etter fylling? Finn kapasitansene til kondensatoren og overflateladningstetthetene på platene før og etter fylling.
| d
|
| d
|
så før og etter fylling har vi
Gitt at s=konst Og d=konst, vi får
![]()
Før og etter fylling med ebonitt har vi
![]()
Overflateladningstetthet
Beregninger:
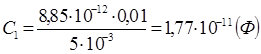
Svar: før og etter fylling med ebonitt har vi
Oppgave 24
Mellom platene flat kondensator, plassert på avstand d=1 cm fra hverandre, påført potensialforskjell U\u003d 100 V. En planparallell plate av krystallinsk thalliumbromid () tykk er ved siden av en av platene. Etter å ha koblet kondensatoren fra spenningskilden, fjernes krystallplaten. Hva blir potensialforskjellen mellom platene til kondensatoren etter dette?
vi kan skrive
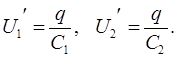
Batterispenningen vil være lik summen av spenningene på de enkelte kondensatorene, dvs.
![]()
Derfor,
Derfor, for kapasiteten MED av hele batteriet vi finner
| MED -q +q d0 e e 01 U 1 |
| С¢ d +q -q e=1 U 2 |
Ved å erstatte (1) med (2), får vi
Kapasitans til kondensatoren i andre posisjon
I henhold til loven om bevaring av ladning q=q¢, dvs.
Beregninger:
Svar: potensialforskjellen blir 1,8 kV.
Oppgave 25
Finn kapasitet MED kondensatorsystemet vist på figuren. Kapasitans til hver kondensator MED\u003d 0,5 uF.
| C1 C3 C2 |
finne C res den resulterende kondensatorbanken.
Tenk på et batteri og en kondensator Fra 3, de er koblet i serie. Å vite det kl seriell tilkobling
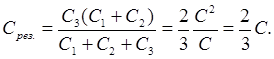
Beregninger:
Svar: kapasitansen til kondensatorsystemet er uF.
Oppgave 26
Kapasitansene til to kondensatorer ble sammenlignet med et elektrometer. For å gjøre dette ble de belastet med potensielle forskjeller U 1=300 V og U 2=100 V og koblet begge kondensatorene parallelt. Potensialforskjellen målt i dette tilfellet mellom kondensatorplatene viste seg å være lik U\u003d 250 V. Finn forholdet mellom kapasiteter
| EN) C1 + - U 1 |
| b) C2
Hvor U- potensialforskjell mellom platene etter tilkobling.
Erstatter verdiene q 1, q 2, q 1 ¢, q 2 ¢ til uttrykk (1), får vi delt på MED 2
Beregninger:
Svar: forholdet mellom kondensatorer Oppgave 27 Plater av en flat kondensator med et område Bytt (2) inn i (1) og uttrykk q Vi erstatter uttrykk (2) med (4), får vi Bytt (5) inn i (6) Beregninger: |
Semester 3. Forelesning4.
Forelesning 4. Elektrisk felt av ladede ledere.
Energien til det elektrostatiske feltet.
Felt nær konduktøren. Kapasitans til ledere og kondensatorer. (Kapasiteter til flate, sylindriske og sfæriske kondensatorer). Energi til et system med faste ladninger. Energien til en ladet leder, kondensator. Elektrostatisk feltenergitetthet.
Når en leder blir introdusert i et eksternt elektrisk felt, begynner ladningene inne i lederen å bevege seg under påvirkning av krefter fra det ytre feltet til likevekt er nådd. Dette fører til en omfordeling av den elektriske ladningen inne i lederen. Regioner av lederen, tidligere elektrisk nøytrale, får en ukompensert elektrisk ladning. Følgelig oppstår et elektrisk felt (eller, som de sier, induseres) i lederen 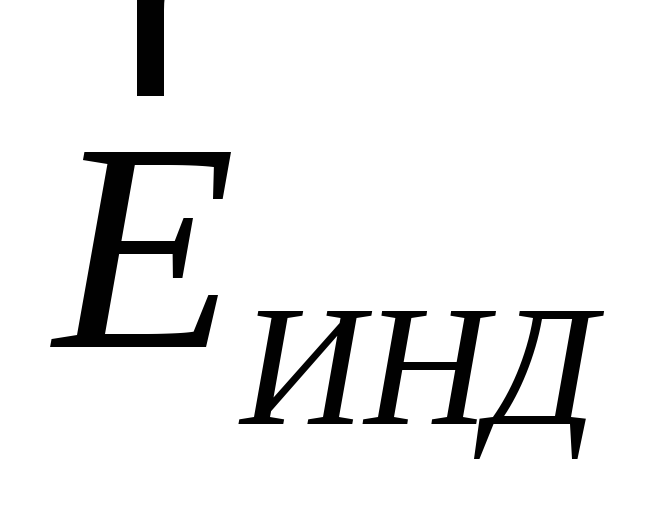 . Betingelsen for likevekt av elektriske ladninger:
. Betingelsen for likevekt av elektriske ladninger:
 ,
,
de. feltstyrke inne i lederen:
Derfor, fra likhet får vi ![]() inne i konduktøren. Derfor er denne betingelsen også oppfylt ved grensen til lederen. De. lederflaten er ekvipotensial
flate
, Derfor kraftlinjer elektrisk felt vinkelrett på overflaten av lederen i hvert punkt
.
inne i konduktøren. Derfor er denne betingelsen også oppfylt ved grensen til lederen. De. lederflaten er ekvipotensial
flate
, Derfor kraftlinjer elektrisk felt vinkelrett på overflaten av lederen i hvert punkt
.
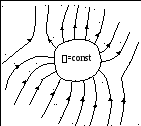
ladet konduktør .
Hvis en ekstern elektrisk ladning blir gitt til en enslig leder, fører betingelsen for likevekt av ladninger igjen til tilstanden:
,![]() inne i konduktøren.
inne i konduktøren.
Det følger at alle eksterne ladninger er plassert på overflaten av lederen, siden. feltstyrken inne i lederen er null, og i henhold til Gauss-teoremet for enhver lukket overflate inne i lederen (inkludert den ytre overflaten av lederen):
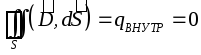 .
.
Siden overflaten til lederen i dette tilfellet også er ekvipotensial, er kraftlinjene til det elektriske feltet rettet vinkelrett på overflaten av lederen på hvert av punktene.
Fra Gauss-teoremet følger det at nær overflaten av lederen
Størrelsen på den elektriske forskyvningsvektoren er lik overflatetettheten til ytre ladninger.
Ladningen på overflaten av lederen er fordelt på en slik måte at overflatepotensialet forblir konstant. Dette fører til det faktum at ladningstettheten på overflaten av lederen ikke er den samme. For eksempel, på de skarpe delene av lederne, er ladningstettheten større enn i utsparingene. I denne forbindelse oppstår det forskjellige fenomener, for eksempel "ladningsavløp". Hvis lederen er i luften, skjer ionisering av luften nær spissen, og bærer bort en del av den elektriske ladningen - et fenomen som kalles "elektrisk vind".
Metode for elektrisk bildebehandling .
Hvis ekvipotensialflaten erstattes av en ledende, og deretter den delen av feltet som denne flaten skiller forkastes, vil ikke feltmønsteret i den gjenværende delen endres. Omvendt, hvis feltbildet er supplert med fiktive ladninger slik at den ledende overflaten kan erstattes med en ekvipotensial, vil ikke det innledende feltbildet endres.
Eksempel.Finn tiltrekningskraften til en punktladning til et uendelig ledende plan
. For å gjøre dette vil vi supplere bildet med en annen ladning av samme type, men av motsatt tegn, plassert symmetrisk i forhold til planet. Da vil flyet falle sammen med ekvipotensialoverflaten, slik at flyet kan forkastes og samspillskraften mellom ladninger kan bli funnet: 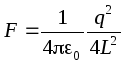 .
.
Energien til en ladet leder .
Energien til en enslig ladet leder er definert som energien til et ladningssystem: 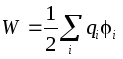 . På lederen, så energien til en enslig leder:
. På lederen, så energien til en enslig leder:
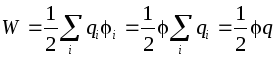 .
.
For et system med ladede ledere: 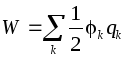 .
.
Spesielt for to ledere som har ladninger q av samme størrelse, men forskjellige i fortegn, vil energien være lik: 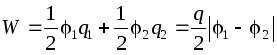 .
.
Kommentar
. Størrelsen på potensialforskjellen ![]() kalt Spenning
mellom kropper.
kalt Spenning
mellom kropper.
Erfaring viser at det er en lineær sammenheng mellom ladningen til en enslig leder og dens potensial: . Proporsjonalitetsfaktor MED kalt koeffisient av elektrisk
beholdere eller elektrisk kapasitet
.
Enheten for elektrisk kapasitet er Farad ( 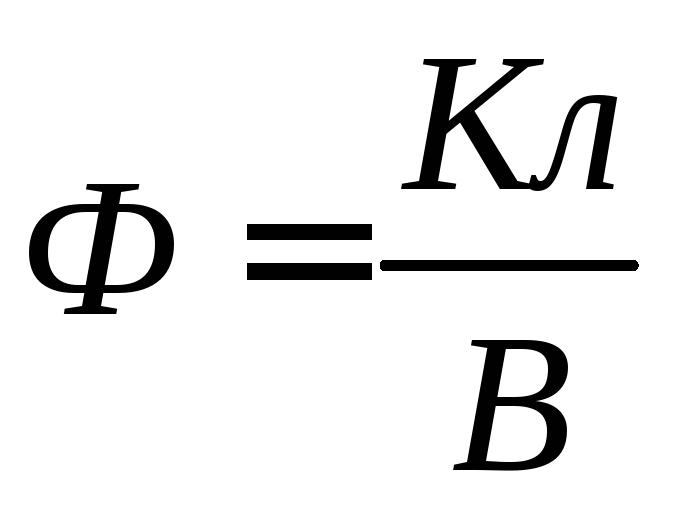 ).
).
Kondensator kalles et system av to ledere ladet med samme styrke, men forskjellige i tegnladninger. Konduktørene kalles kondensatorplater .
Kapasitansen til en kondensator bestemmes av formelen.
Kondensatoren er konvensjonelt utpekt.
Tilkobling av kondensatorer
Tenk på en seriekobling av to kondensatorer C 1 og C 2. Punkt A mellom kondensatorene er atskilt fra resten av kretsen, så dens elektriske ladning kan ikke endres. Siden den opprinnelige ladningen til et hvilket som helst punkt var lik null, da ![]() . Følgelig er ladningene til kondensatorplatene ved siden av punkt A like store, men motsatt i fortegn. Men siden verdien av ladningen til platene er lik ladningen til kondensatorene, da. Den totale ladningen til punkt A er null, så hvis vi forkaster dette punktet sammen med platene, vil ingenting endre seg i kretsen. Fordi ladningene til de ekstreme platene er også de samme i størrelse, men forskjellige i fortegn, da vil den resulterende kondensatoren ha samme ladning i størrelse.
. Følgelig er ladningene til kondensatorplatene ved siden av punkt A like store, men motsatt i fortegn. Men siden verdien av ladningen til platene er lik ladningen til kondensatorene, da. Den totale ladningen til punkt A er null, så hvis vi forkaster dette punktet sammen med platene, vil ingenting endre seg i kretsen. Fordi ladningene til de ekstreme platene er også de samme i størrelse, men forskjellige i fortegn, da vil den resulterende kondensatoren ha samme ladning i størrelse.
TOTAL . Ladningene til kondensatorer koblet i serie er de samme i størrelsesorden. Den totale ladningen til kondensatorene koblet i serie er lik ladningen til hver av kondensatorene.
For dette tilfellet er den totale spenningen lik summen av spenningene på kondensatorene: U GENERELT \u003d U 1 + U 2. Ladningene til kondensatorene er de samme: q 1 \u003d q 2 \u003d q. Deretter 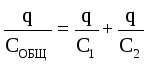 . Derfor
. Derfor 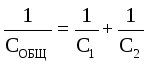 .
.
Når kondensatorer er koblet i serie, blir deres kapasitans lagt til i henhold til loven om gjensidighet .
Kapasitansberegning for parallellkobling av kondensatorer.
For dette tilfellet er spenningene på kondensatorene de samme: U 1 \u003d U 2 \u003d U.
Den totale ladningen er lik summen av ladningene: q GEN = q 1 + q 2 eller C GEN U=C 1 U+C 2 U.
Så C GENERELT =C 1 + C 2 . Når kondensatorer er koblet parallelt, summeres kapasitansene deres.
Kondensator energi :
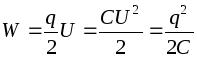 .
.
Den totale ladningen til kondensatoren er null. En kondensator lagrer elektrisk energi ved å separere elektriske ladninger.
Eksempler for beregning av kapasitans til kondensatorer .
Flat (luft) kondensator representerer to parallelle plater, hvor avstanden mellom disse er mye mindre enn dimensjonene til platene, slik at feltet mellom platene kan anses som ensartet. Det er et vakuum (luft) mellom platene, derfor = 1.
 I dette tilfellet, når man beregner feltmønsteret, kan man bruke resultatene oppnådd for feltet til et uendelig ladet plan. Siden ladningene og arealene til platene er like i størrelse, er størrelsen på feltstyrken skapt av hver av platene den samme: men retningene til intensitetsvektorene er forskjellige (intensitetsvektoren fra en negativt ladet plate er vist av en stiplet linje). Mellom platene er intensitetsvektorene rettet på samme måte, så den totale intensiteten er lik summen av feltstyrkene skapt av hver av platene:
I dette tilfellet, når man beregner feltmønsteret, kan man bruke resultatene oppnådd for feltet til et uendelig ladet plan. Siden ladningene og arealene til platene er like i størrelse, er størrelsen på feltstyrken skapt av hver av platene den samme: men retningene til intensitetsvektorene er forskjellige (intensitetsvektoren fra en negativt ladet plate er vist av en stiplet linje). Mellom platene er intensitetsvektorene rettet på samme måte, så den totale intensiteten er lik summen av feltstyrkene skapt av hver av platene:
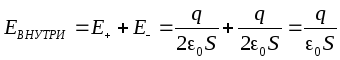 .
.
Utenfor platene er feltstyrkevektorene rettet motsatt, så feltstyrken utenfor er null. Dermed, i en kondensator er feltstyrken ikke null bare mellom platene.
Siden det elektrostatiske feltet er et felt med konservativ kraft, er integralet 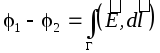 er ikke avhengig av formen på banen G, slik at potensialforskjellen mellom platene kan finnes langs perpendikulæren som forbinder platene, hvis lengde er lik d:
er ikke avhengig av formen på banen G, slik at potensialforskjellen mellom platene kan finnes langs perpendikulæren som forbinder platene, hvis lengde er lik d: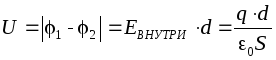 , Hvor d er avstanden mellom platene. Da vil kapasitansen til en flat (luft) kondensator i samsvar med definisjonen være lik:
, Hvor d er avstanden mellom platene. Da vil kapasitansen til en flat (luft) kondensator i samsvar med definisjonen være lik: 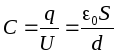
Sylindrisk (luft) kondensator består av to koaksiale sylindre
av samme lengde, nestet i hverandre slik at avstanden mellom platene er mye mindre enn dimensjonene til platene.
La lengden på kondensatoren L, ladningen til den indre foringen er positiv: q > 0. Pletteringsradier R 1 og R 2, la R 1 <R 2. Feltstyrke mellom platene på avstand r fra innerforet, dvs. Til R 1 <r <R 2 finner vi ved å bruke Gauss-teoremet:
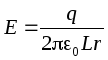 .
.
Deretter spenningen mellom platene: .
Derfor er den elektriske kapasiteten til en sylindrisk (luft) kondensator: ![]() .
.
MED  sfærisk (luft) kondensator
representerer to nestede konsentriske kuler med radiene til platene R 1 og R 2 ,R 1 <R 2. La ladningen til den indre foringen q> 0. Feltstyrken mellom foringene på avstand r fra den indre foringen ( R 1
<r
<R 2) vi finner ved Gauss-teoremet:
sfærisk (luft) kondensator
representerer to nestede konsentriske kuler med radiene til platene R 1 og R 2 ,R 1 <R 2. La ladningen til den indre foringen q> 0. Feltstyrken mellom foringene på avstand r fra den indre foringen ( R 1
<r
<R 2) vi finner ved Gauss-teoremet:
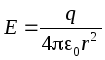 .
.
Spenning mellom plater:.
Derfor er kapasitansen til en sfærisk (luft) kondensator ![]() .
.
Volumetrisk energitetthet av det elektrostatiske feltet.
Vurder en flat luftkondensator. Energi til en ladet kondensator
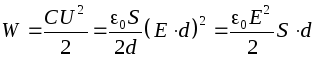 .
.
Mengden plass mellom platene til en kondensator. Siden feltet mellom platene anses å være homogent, har enhetsvolumet til dette feltet energien 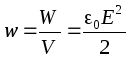 . Denne verdien kalles volumetrisk energitetthet
.
. Denne verdien kalles volumetrisk energitetthet
.
I tilfellet når feltet ikke er jevnt, er den volumetriske energitettheten .
I materie, den volumetriske energitettheten til det elektriske feltet 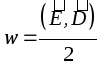 .
.
I tilfelle av et homogent isotropisk dielektrisk, derfor 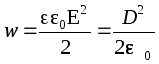 .
.
Fordi ![]() , Det
, Det 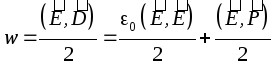 , Hvor
, Hvor
Energien til det elektriske feltet i vakuum er energien til polarisasjonen av materie.
Eksempel . Tenk på en ladet tynnvegget kule med radius R. Siden ladninger med samme navn frastøter hverandre på sfæren, har frastøtende krefter en tendens til å strekke overflaten av sfæren. Vi kan anta at fra innsiden av kulen påvirkes veggene av tilleggstrykk s, sprengning av kulen og forårsaket av tilstedeværelsen av en elektrisk ladning på overflaten. La oss finne R.
Feltstyrken inne i sfæren er null, så volumenergitettheten til det elektriske feltet w er forskjellig fra null bare utenfor sfæren.
Med en liten økning i kulens radius med dR volumet vil øke, mens i den delen av det omkringliggende rommet som kom inn i kulen, vil den volumetriske energitettheten bli lik null. Derfor vil endringen i energien til feltet utenfor være lik, hvor S er overflatearealet. Men med utvidelsen av sfæren vil trykkkreftene inne i sfæren gjøre jobben ![]() . Siden da
. Siden da ![]() hvorfra.
hvorfra.
Eksempel . La oss finne kreftene som virker på platene i en ladet flat kondensator, koblet fra strømkilden.
Platene er motsatt ladet, så de tiltrekker seg. Anta at platene er en liten mengde nær hverandre. x. Deretter reduseres volumet av kondensatoren med dV = xS, så energien til kondensatoren har redusert med dW = wdV. Attraktive krefter virker EN = f.eks. Siden A= dW, Det f.eks = wxS. Derfor er størrelsen på kraften F = wS. Ekstratrykket som disse kreftene skaper er lik.
Eksemplene ovenfor viser at legemer i et elektrisk felt er utsatt for krefter som forårsaker ytterligere trykk lik den volumetriske energitettheten.
Trykket forårsaket av tilstedeværelsen av et elektrisk felt er lik den volumetriske energitettheten .
Krefter , som virker på kroppen fra siden av et felt, kalles pondemotor .
De motsatt ladede kondensatorplatene tiltrekker hverandre.
Mekaniske krefter som virker på makroskopiske ladede legemer kallestankevekkende .
Vi beregner de ponderomotive kreftene som virker på platene til en flat kondensator. I dette tilfellet er to alternativer mulig:
Kondensatoren lades og kobles fra det ladede batteriet(i dette tilfellet forblir antall ladninger på platene konstant q = konst).
Når en plate av en kondensator fjernes fra den andre, er arbeidet gjort
på grunn av hvilken den potensielle energien til systemet øker:
I dette tilfellet er dA = dW . Ved å likestille høyresidene av disse uttrykkene får vi
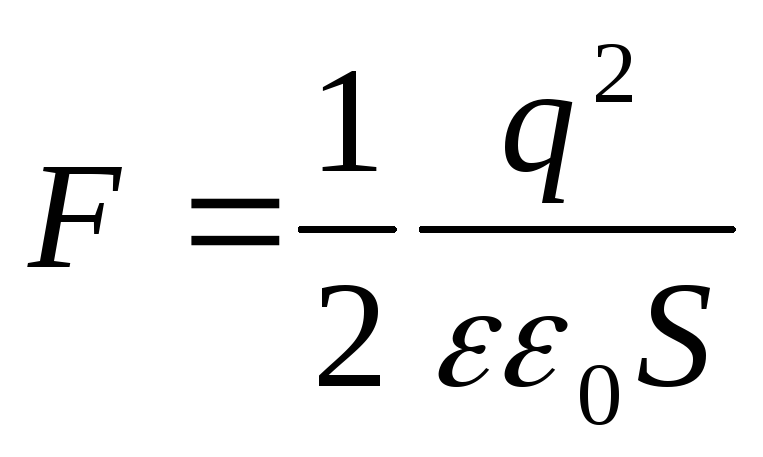 (12.67)
(12.67)
I dette tilfellet, ved differensiering, ble avstanden mellom platene betegnet x.
Kondensator ladet, men ikke koblet fra batteriet(i dette tilfellet, når du flytter en av kondensatorplatene, vil spenningen forbli konstant ( U = konst). I dette tilfellet, når en plate beveger seg bort fra den andre, reduseres den potensielle energien til kondensatorfeltet, siden ladninger "lekker" fra platene, derfor
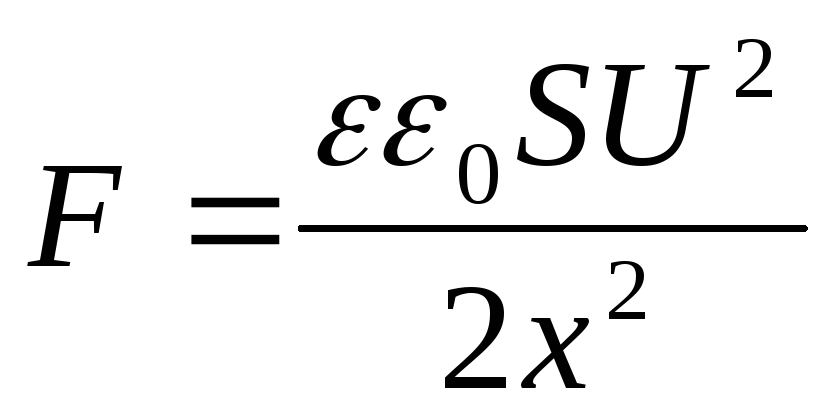
Men 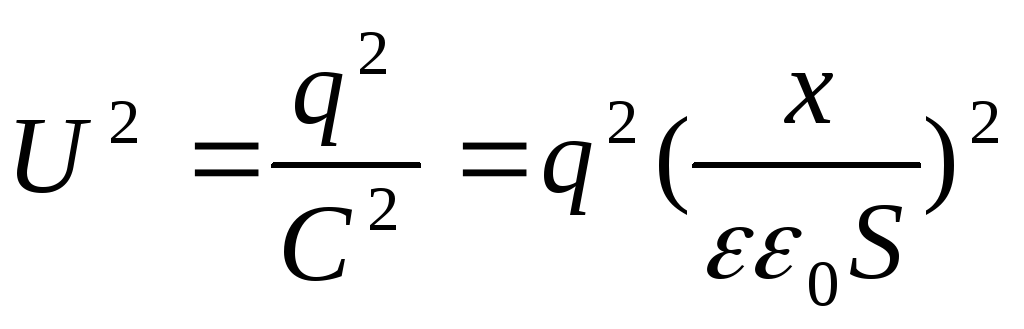 , Deretter
, Deretter
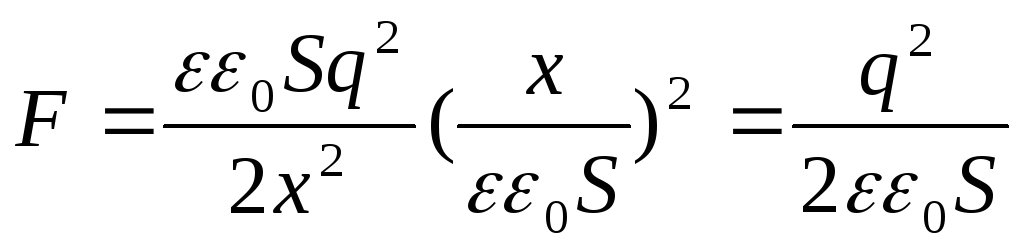
Det resulterende uttrykket faller sammen med formelen 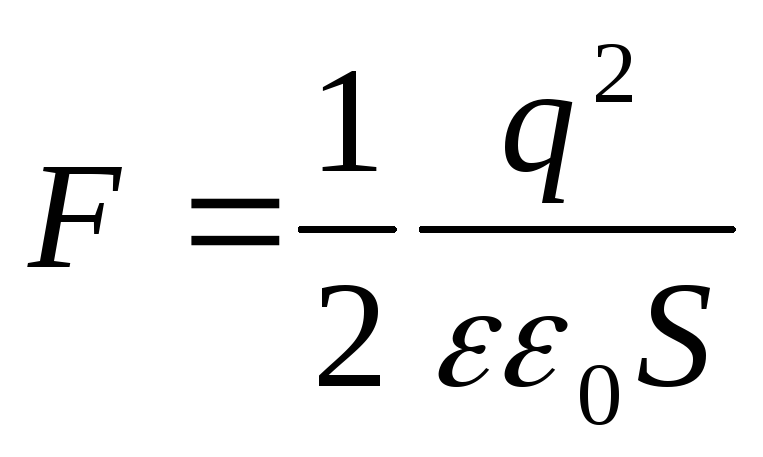 . Det kan også representeres i en annen form hvis vi i stedet for ladningen q introduserer overflatetettheten:
. Det kan også representeres i en annen form hvis vi i stedet for ladningen q introduserer overflatetettheten:
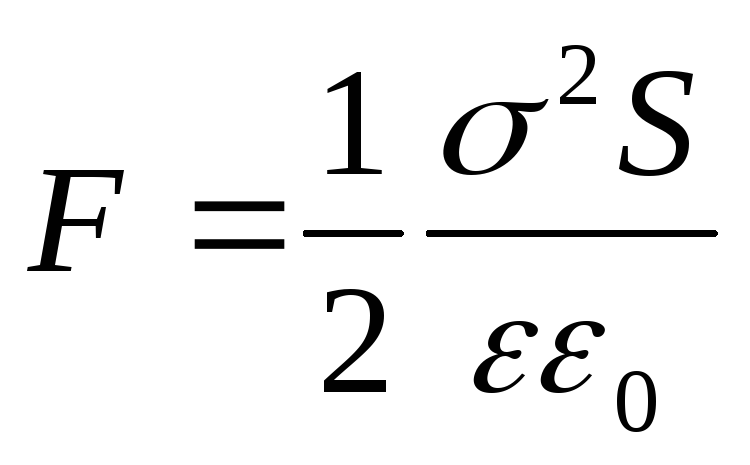 (12.68)
(12.68)
Feltet er enhetlig. Feltstyrken til kondensatoren er 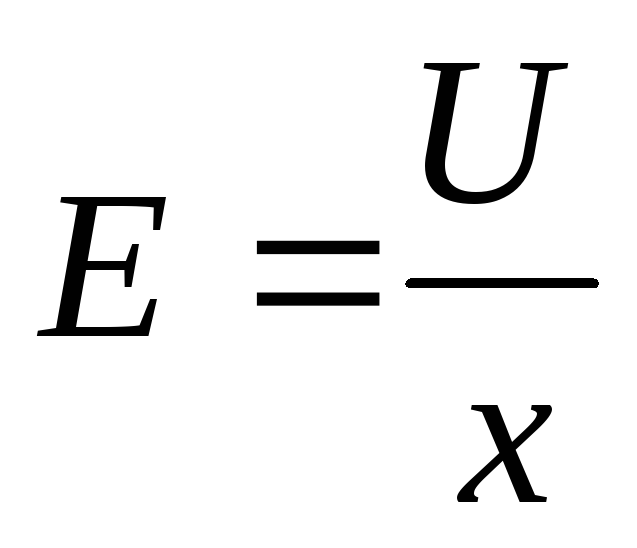 , hvor x er avstanden mellom platene. Bytter inn i formelen
, hvor x er avstanden mellom platene. Bytter inn i formelen 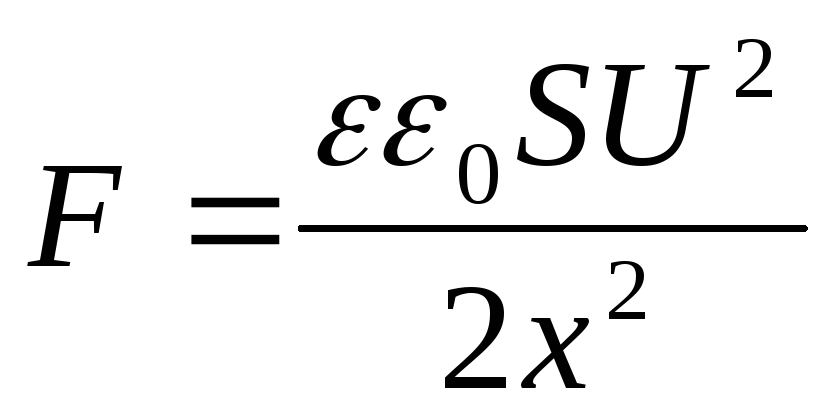 U 2 \u003d E 2 x 2, får vi at tiltrekningskraften til platene til en flat kondensator
U 2 \u003d E 2 x 2, får vi at tiltrekningskraften til platene til en flat kondensator
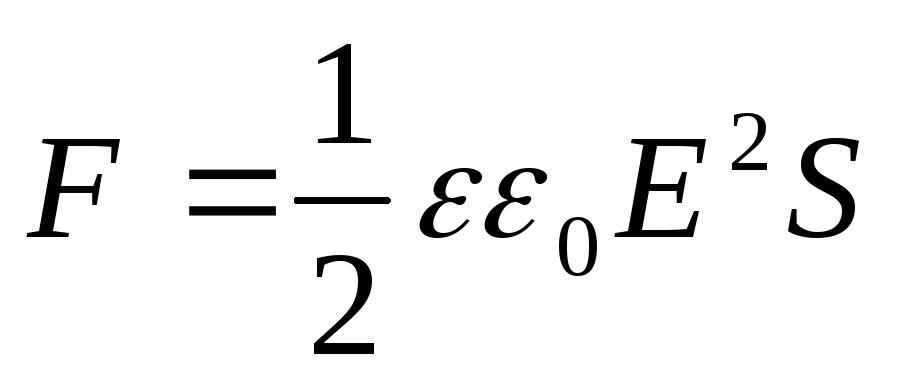 (12.69)
(12.69)
Disse kreftene virker ikke bare på platene. Siden platene på sin side legger press på dielektrikumet plassert mellom dem og deformerer det, oppstår det trykk i dielektrikumet
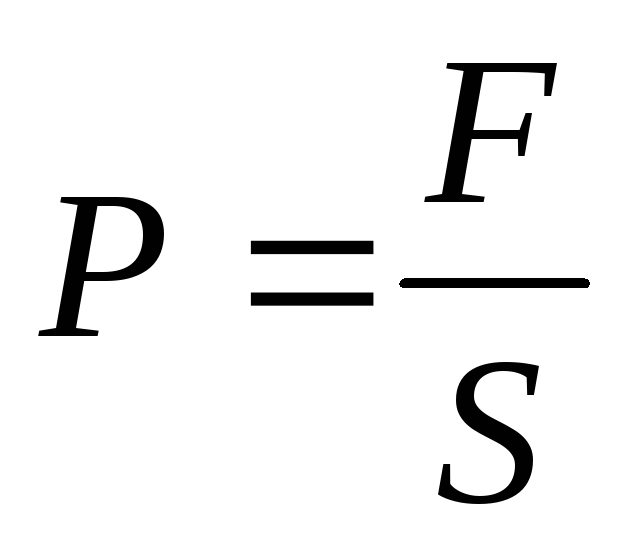
(S er arealet av hver plate).
Trykket som oppstår i dielektrikumet er
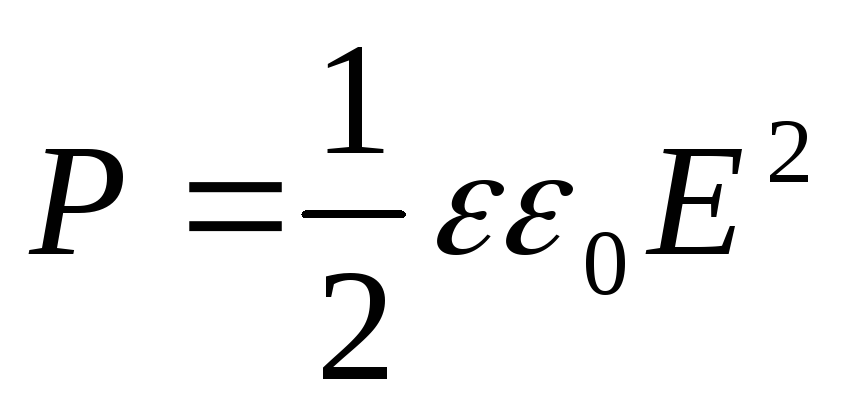 (12.70)
(12.70)
Eksempler på problemløsning
Eksempel 12.5. En potensialforskjell på 1,5 kV påføres platene til en flat luftkondensator. Plateareal 150 cm 2 og avstanden mellom dem er 5 mm. Etter å ha koblet kondensatoren fra spenningskilden, ble glass satt inn i rommet mellom platene (ε 2 =7). Definer:
1) potensialforskjell mellom platene etter introduksjonen av et dielektrikum; 2) kapasitansen til kondensatoren før og etter introduksjonen av dielektrikumet; 3) overflateladningstettheten på platene før og etter introduksjonen av dielektrikumet.
Gitt: U 1 \u003d 1,5 kV \u003d 1,5 ∙ 10 3 V; S \u003d 150cm 2 \u003d 1,5 ∙ 10 -2 m 2; e 1 = 1; d=5mm=5∙10 -3 m.
Finn: 1) U 2 ; 2) C1C2; 3) σ 1 , σ 2
Løsning
.
Fordi 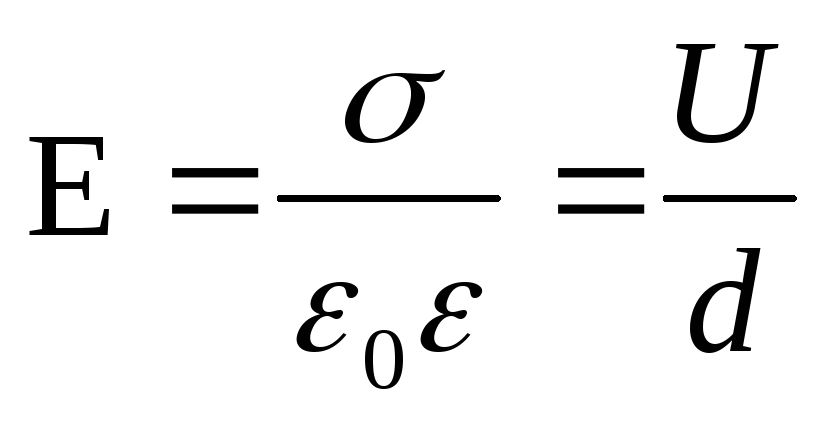 (σ er overflateladningstettheten på kondensatorplatene), så før introduksjonen av dielektrikumet σd=U 1 ε 0 ε 1 og etter introduksjonen av dielektrikumet σd=U 2 ε 0 ε 2, derfor
(σ er overflateladningstettheten på kondensatorplatene), så før introduksjonen av dielektrikumet σd=U 1 ε 0 ε 1 og etter introduksjonen av dielektrikumet σd=U 2 ε 0 ε 2, derfor
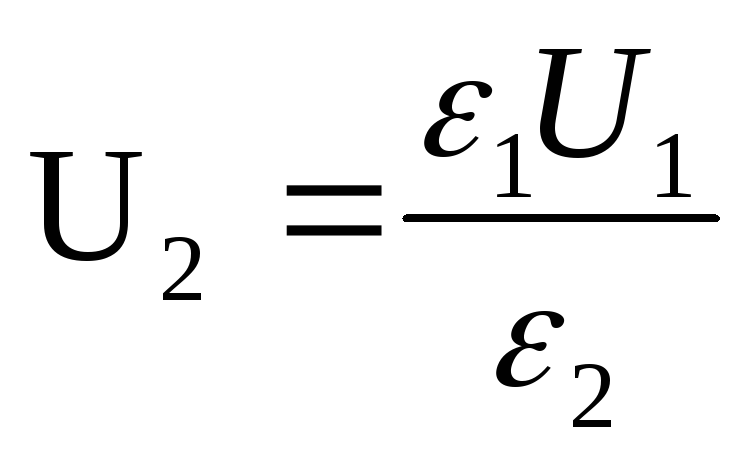
Kapasitansen til kondensatoren før og etter introduksjonen av et dielektrikum
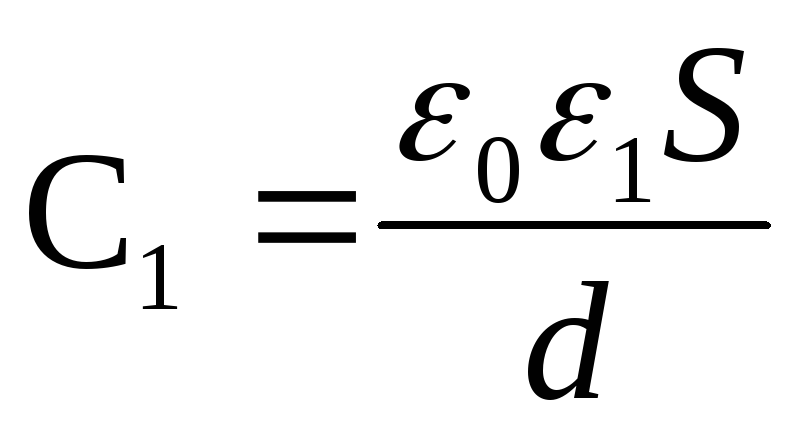 Og
Og 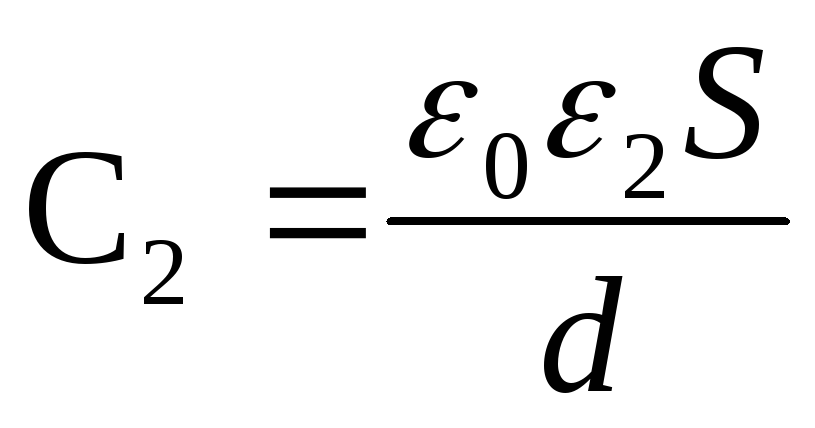
Ladingen av platene etter frakobling fra spenningskilden endres ikke, d.v.s. q=konst. Derfor er overflateladningstettheten på platene før og etter introduksjonen av dielektrikumet
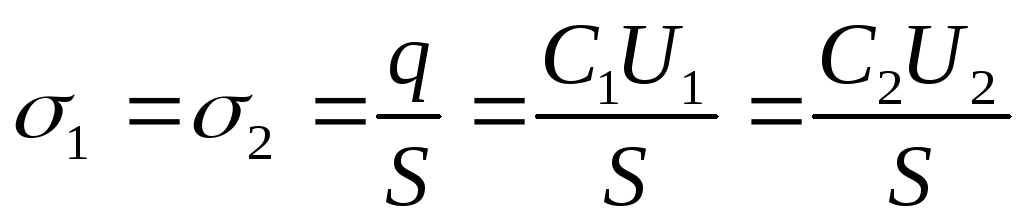
Svar: 1) U 2 \u003d 214V; 2) C 1 \u003d 26,5 pF; C 2 \u003d 186pF; 3) σ 1 = σ 2 = 2,65 μC/m 2.
Eksempel 12.7. Gapet mellom platene til en flat kondensator er fylt med et anisotropisk dielektrikum, hvis permeabilitet ε varierer i retningen vinkelrett på platene i henhold til den lineære lovenε = α + βх fra ε 1 opp til ε 2 og e 2 > ε 1 . Området til hver foringS, avstanden mellom demd. Finn kapasitansen til kondensatoren.
Gitt:S; d; e 1; ε 2
Finne: MED.
Løsning
.
Den dielektriske konstanten ε
varierer lineært, ε = α + βx, hvor x måles fra foringen, hvis permeabilitet er lik ε 1 . Tatt i betraktning at ε (0) = ε 1 , ε (d) = ε 2 , får vi avhengigheten 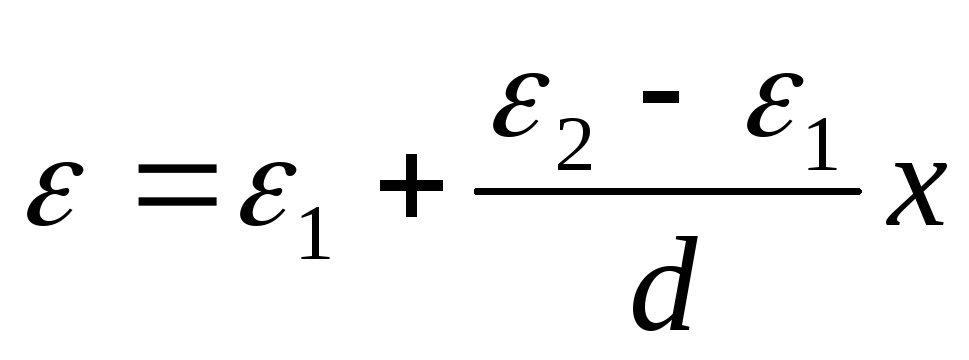 . Finn potensialforskjellen mellom platene:
. Finn potensialforskjellen mellom platene:
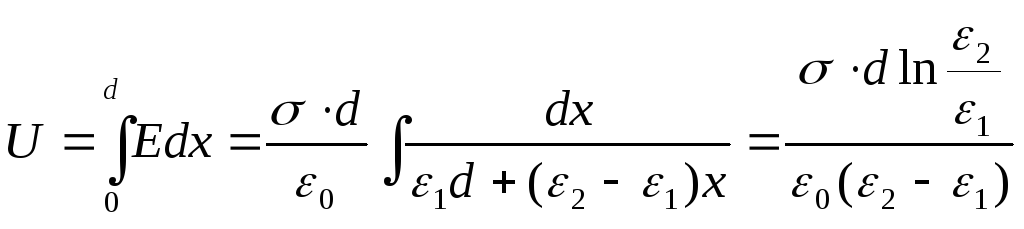
Kapasitansen til kondensatoren vil være
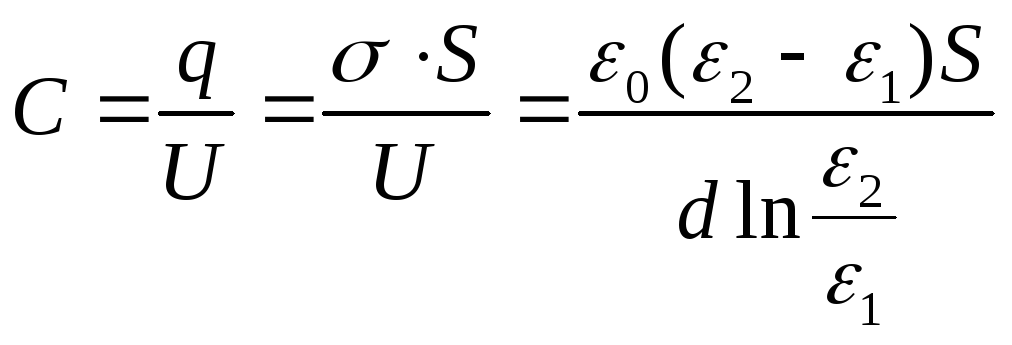
Svar:
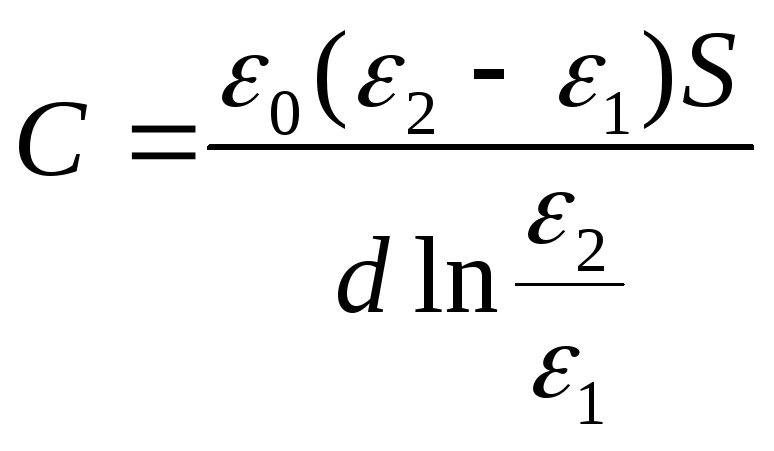
Eksempel 12.7. Mellom platene til en flat kondensator ladet til en potensiell forskjell U , er to lag med dielektrikum plassert parallelt med platene. Tykkelsen på lagene og permittiviteten til dielektrikum er hhv.d 1 , d 2 , ε 1 , ε 2 . Bestem styrken til elektrostatiske felt i dielektriske lag.
Gitt: U; d 1 , d 2 , ε 1 , ε 2
Finne: E1, E2.
Løsning . Spenningen over kondensatorplatene, gitt at feltet innenfor hvert av de dielektriske lagene er ensartet,
U=E1d1+E2d2. (1)
Den elektriske forskyvningen i begge dielektriske lagene er den samme, så vi kan skrive
D=D1=D2= ε 0 ε 1 E 1 = ε 0 ε 2 E 2 (2)
Fra uttrykk (1) og (2) finner vi ønsket
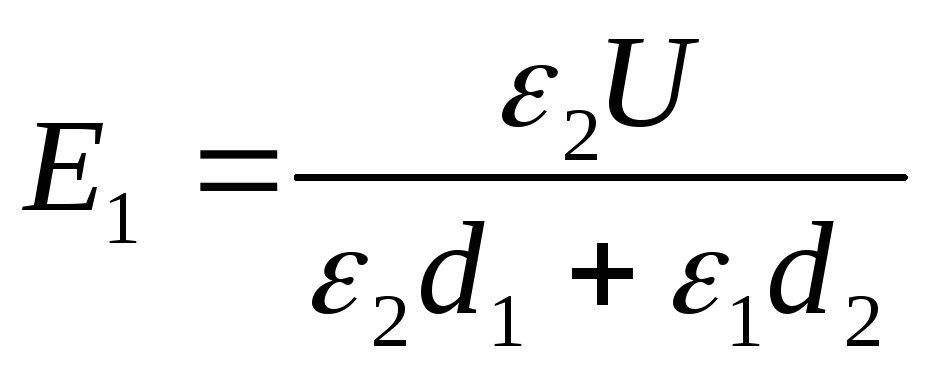 (3)
(3)
Av formel (2) følger det at
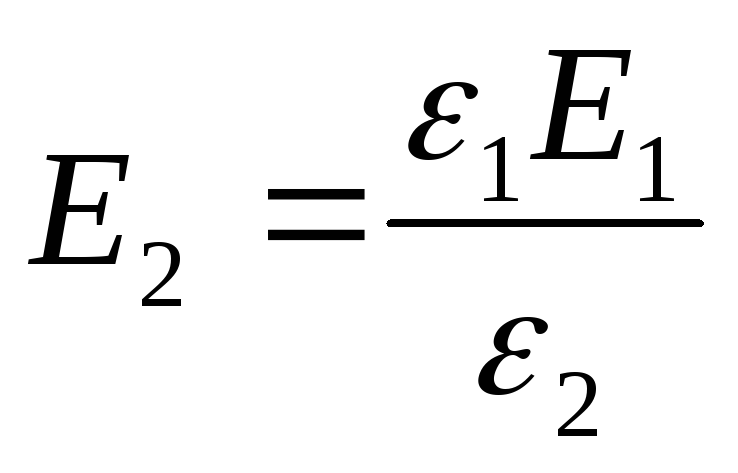
Svar:
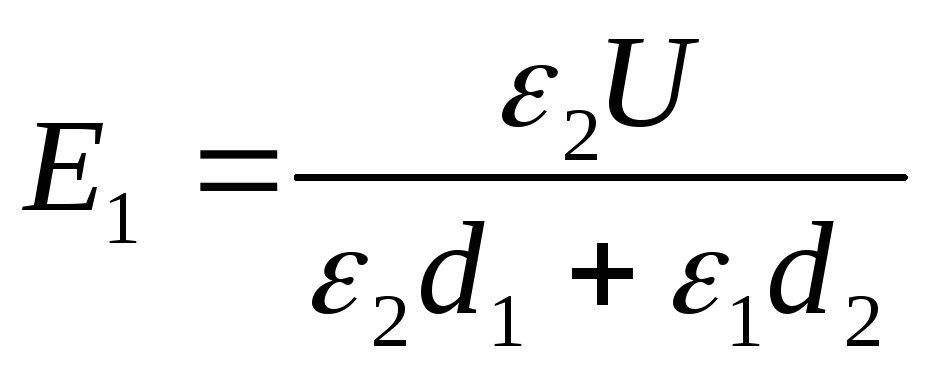 ;
;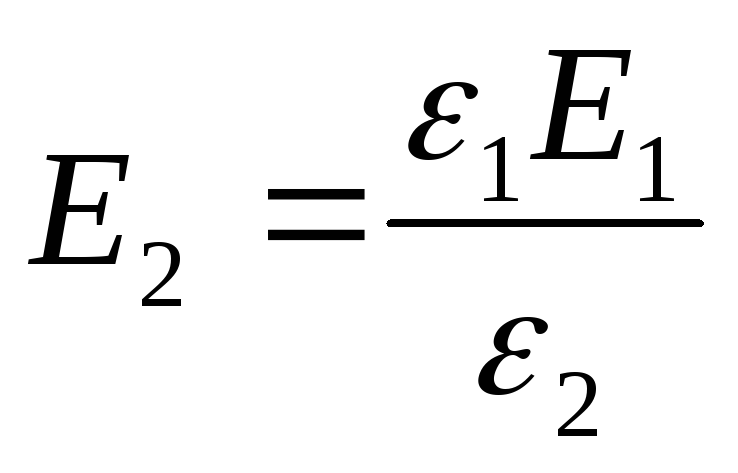
Eksempel 12.7. Plateområde S flat kondensator er 100cm 2 . Rommet mellom platene er tett fylt med to lag med dielektrikum - en glimmerplate (ε 1 =7) tykk d 1 =3,5 mm og parafin (ε 2 =2) tykkelse d 2 =5 mm. Bestem kapasitansen til denne kondensatoren.
Gitt: S= 100 cm 2 =10 -2 m 2 ; ε 1 =7; d 1 =3,5 mm=3,5∙10 -3 m;, e 1 =2; d 1 =3,5 mm=5∙10 -3 m;
Finne: MED.
Løsning . Kondensatorkapasitet
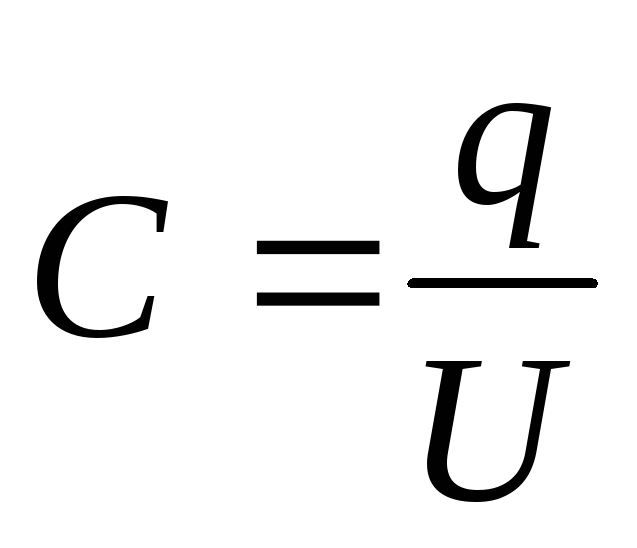
hvor = - ladning på kondensatorplatene (- overflateladningstetthet på platene); \u003d - potensialforskjellen til platene, lik summen av spenningene på de dielektriske lagene: U \u003d U 1 +U 2. Deretter
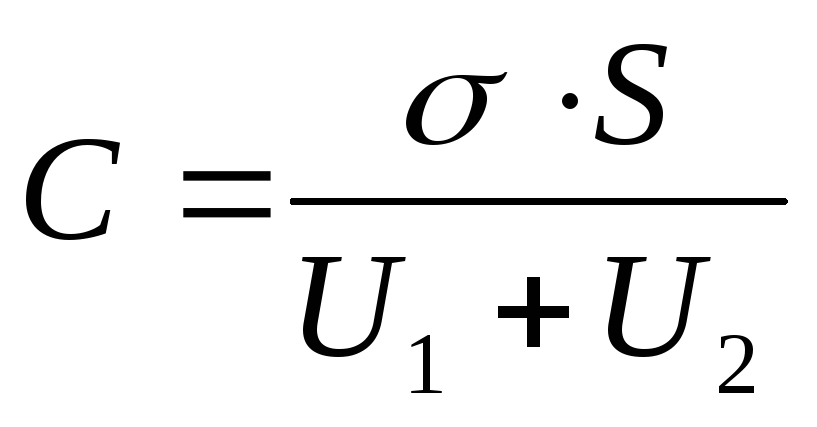 (1)
(1)
Spenningene U 1 og U 2 vil bli funnet av formlene
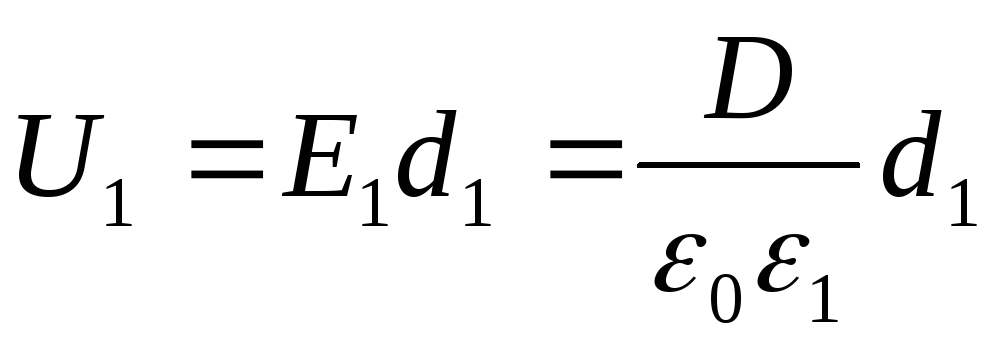 ;
;
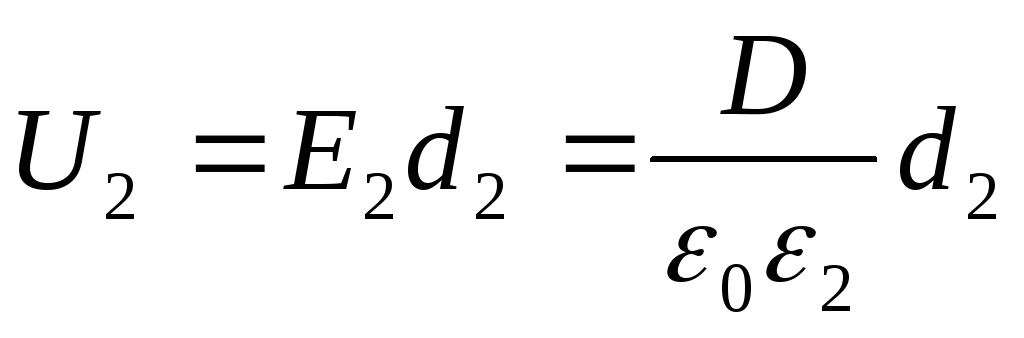 (2)
(2)
hvor E 1 og E 2 - styrken til det elektrostatiske feltet i det første og andre laget av dielektrikumet; D er den elektriske forskyvningen i dielektrikum (det samme i begge tilfeller). Med tanke på det
Og gitt formel (2), fra uttrykk (1) finner vi ønsket kapasitans til kondensatoren
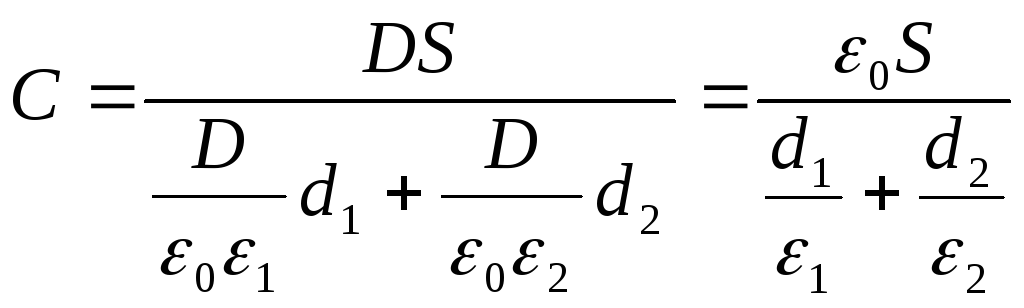
Svar: C \u003d 29,5pF.
Eksempel 12.7. Et batteri med tre kondensatorer koblet i serie C 1 \u003d 1 μF; MED 2 \u003d 2uF og C 3 \u003d 4 μF er koblet til en EMF-kilde. Lading av kondensatorbatteri q \u003d 40 μC. Bestem: 1) spenning U 1 , U 2 Og U 3 på hver kondensator; 2) EMF-kilde; 3) kapasiteten til kondensatorbanken.
Gitt : C 1 \u003d 1 μF \u003d 1 ∙ 10 -6 F; C 2 \u003d 2 μF \u003d 2 ∙ 10 -6 F og C 3 \u003d 4 μF \u003d 4 ∙ 10 -6 F; q \u003d 40 μC \u003d 40 - ∙ F .
Finn: 1) U 1 , U 2 , U 3 ; 2) ξ; 3) C.
Løsning . Når kondensatorer er koblet i serie, er ladningene til alle plater like i absolutt verdi, derfor
q 1 \u003d q 2 \u003d q 3 \u003d q.
Kondensatorspenning
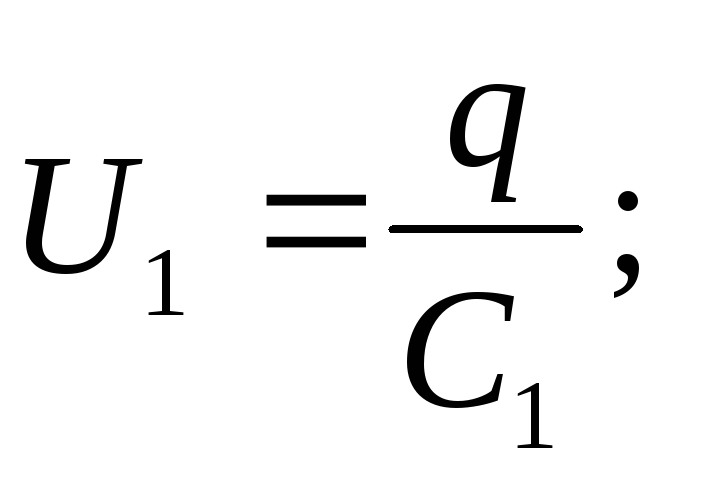
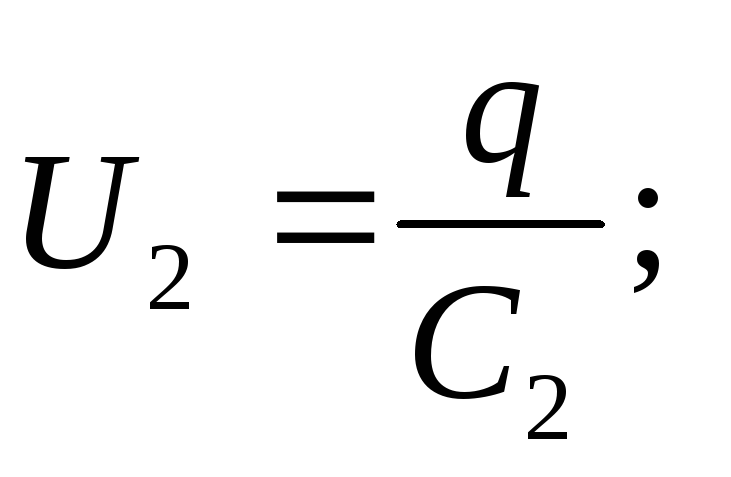
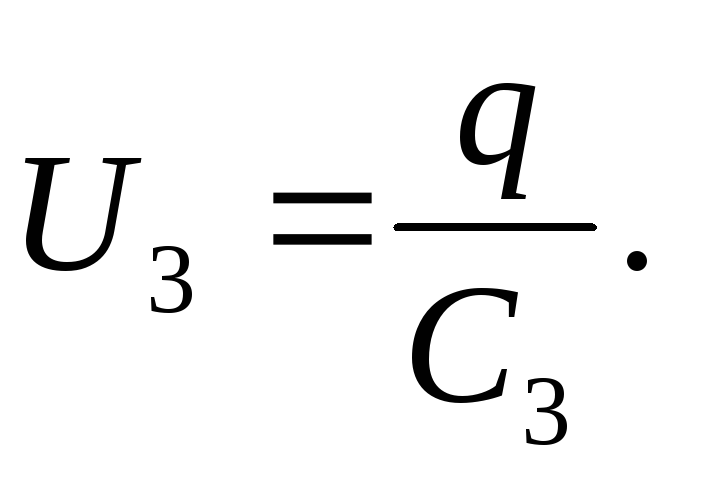
Kildens EMF er lik summen av spenningene til hver av de seriekoblede kondensatorene:
ξ \u003d U 1 + U 2 + U 3
Når de er koblet i serie, summeres resiproka til kapasitansene til hver av kondensatorene:
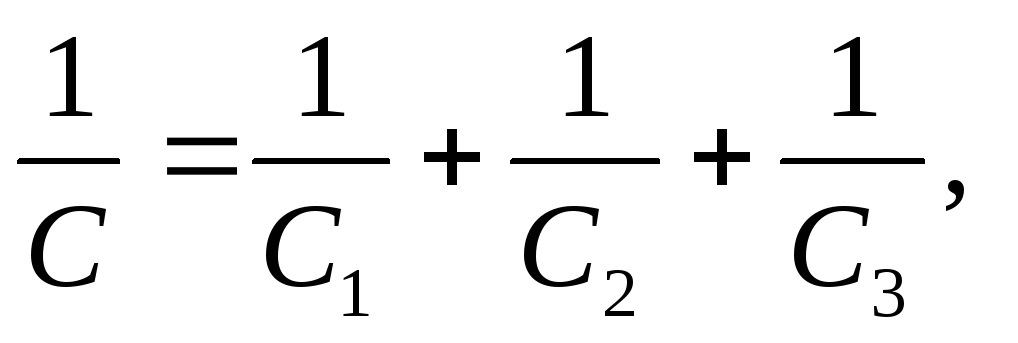
Hvor er ønsket kapasitet til kondensatorbanken
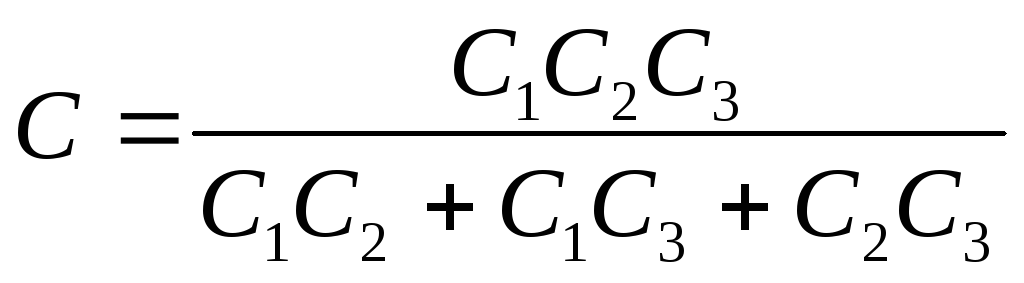
Svar: 1) U 1 \u003d 40V; U 2 \u003d 20V, U 3 = 10V; 2) Ɛ= 70V; 3) C \u003d 0,571 μF.
Eksempel 12.7. To flate luftkondensatorer med samme kapasitet er koblet i serie og koblet til en EMF-kilde. Hvordan og hvor mange ganger vil ladningen til kondensatorer endres hvis en av dem er nedsenket i olje med en dielektrisk konstant ε=2,2.
Gitt: C 1 \u003d C 2 \u003d C; q \u003d 40 μC \u003d 40 ∙ 10 -6 F ; ε 1 =1; ε 2 =2,2.
Finne:
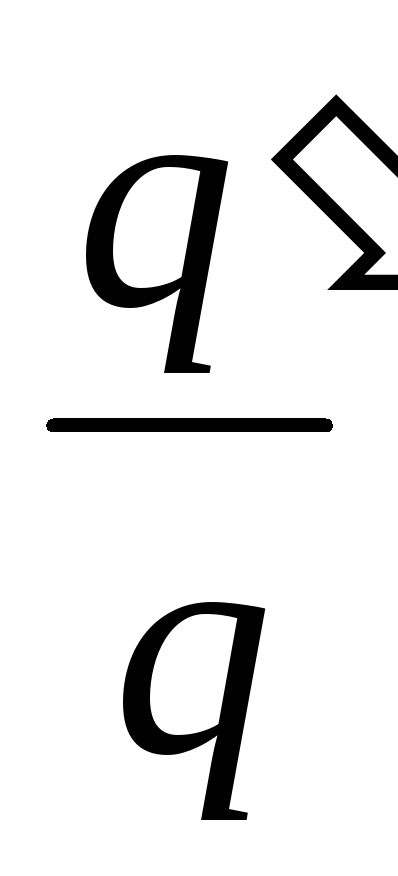 .
.
Løsning . Når kondensatorer er koblet i serie, er ladningene til begge kondensatorene like store. Før nedsenking i et dielektrikum (i olje), ladningen til hver kondensator
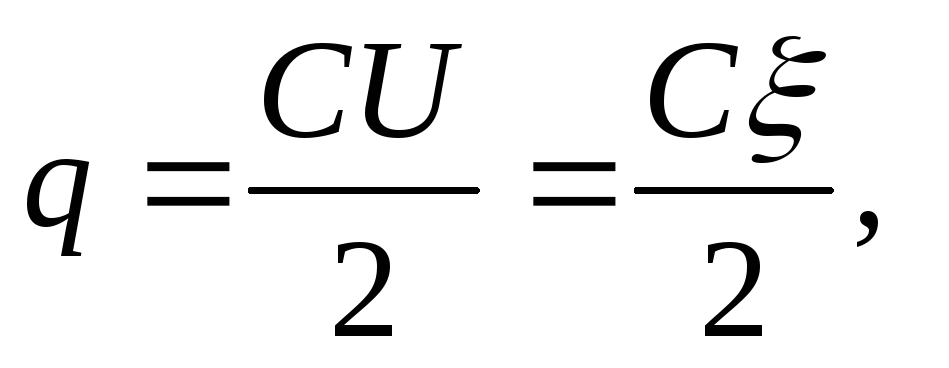
hvor ξ \u003d U 1 + U 2 (når kondensatorer er koblet i serie, er EMF til kilden lik summen av spenningene til hver av kondensatorene).
Etter at en av kondensatorene er nedsenket i et dielektrikum, er ladningene til kondensatorene igjen de samme, og følgelig er den første og andre kondensatoren like
q= CU 1 =ε 2 CU 2
(tar i betraktning at ε 1 =1), hvorav, hvis vi tar i betraktning at ξ = U 1 + U 2, finner vi
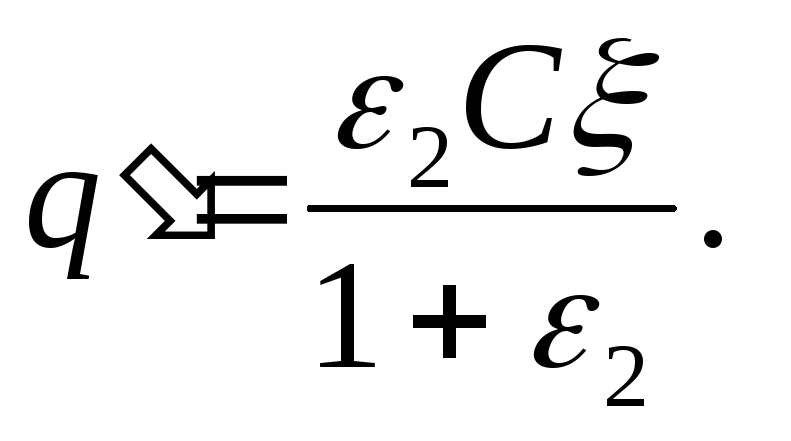 (2)
(2)
Ved å dele (2) med (1), finner vi ønsket forhold
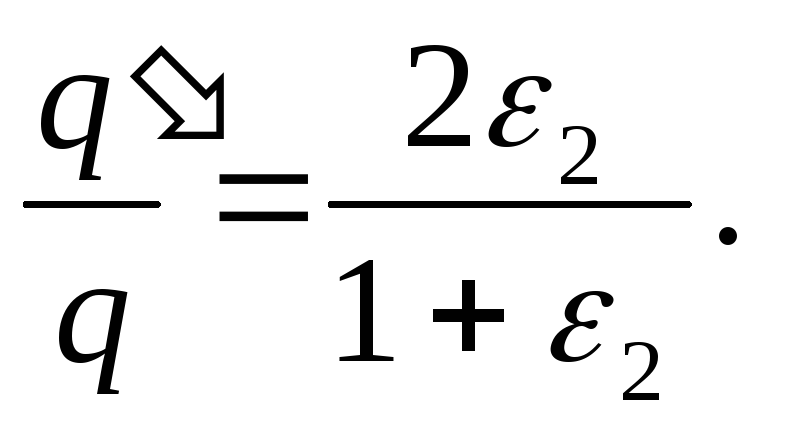
Svar:
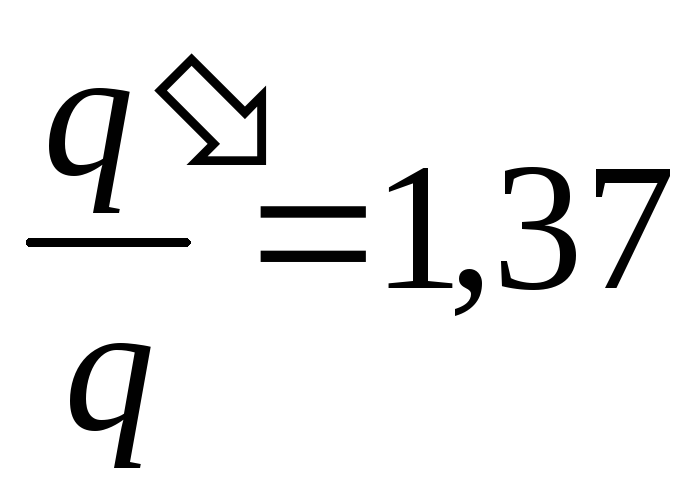 , dvs. ladningen til kondensatorene øker med en faktor på 1,37.
, dvs. ladningen til kondensatorene øker med en faktor på 1,37.
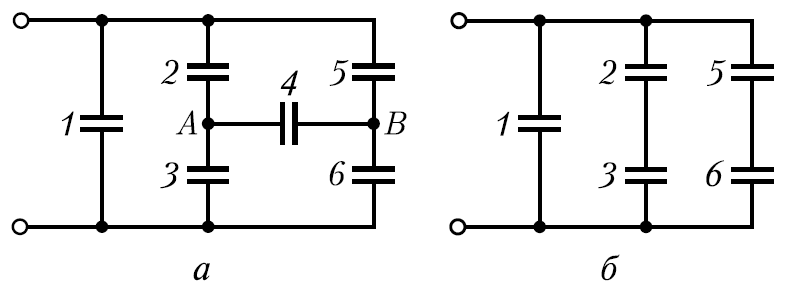
Eksempel 12.7. Kondensatorer med hver kapasitans C kobles til som vist i fig.a. bestemme kapasitansen felles denne tilkoblingen av kondensatorer. .
 Løsning
.
Kobler du kondensator C 4 fra kretsen får du en tilkobling av kondensatorer, som enkelt beregnes. Siden kapasiteten til alle kondensatorene er de samme (C 2 \u003d C 3 og C 5 \u003d C 6), er begge parallelle grener symmetriske, derfor må potensialene til punktene A og B, like plassert i grenene, være like. Kondensator C 4 er dermed koblet til punkter med null potensialforskjell. Derfor er kondensatoren C 4 ikke ladet, dvs. det kan utelukkes og ordningen presentert i tilstanden til problemet kan forenkles (fig. b).
Løsning
.
Kobler du kondensator C 4 fra kretsen får du en tilkobling av kondensatorer, som enkelt beregnes. Siden kapasiteten til alle kondensatorene er de samme (C 2 \u003d C 3 og C 5 \u003d C 6), er begge parallelle grener symmetriske, derfor må potensialene til punktene A og B, like plassert i grenene, være like. Kondensator C 4 er dermed koblet til punkter med null potensialforskjell. Derfor er kondensatoren C 4 ikke ladet, dvs. det kan utelukkes og ordningen presentert i tilstanden til problemet kan forenkles (fig. b).
Denne kretsen består av tre parallelle grener, hvorav to inneholder to kondensatorer i serie.
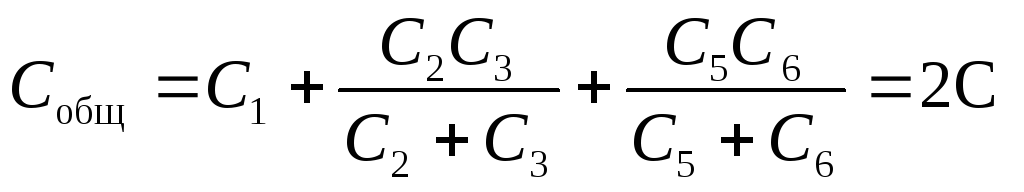
Svar: C totalt = 2C.
Eksempel 12.7. Flat luftkondensator med kapasitet C 1 \u003d 4pF ladet til en potensiell forskjellU 1 =100V. Etter å ha koblet kondensatoren fra spenningskilden, ble avstanden mellom kondensatorplatene doblet. Bestem: 1) potensialforskjellU 2 på kondensatorplatene etter at de er separert; 2) arbeidet med ytre krefter for å skyve platene fra hverandre.
Gitt: C 1 \u003d 4pF \u003d 4 ∙ 10 -12 F; U 1 \u003d 100V; d 2 \u003d 2d 1.
Finne: 1) U 2 ;2)A.
Løsning . Ladningen av kondensatorplatene etter frakobling fra spenningskilden endres ikke, dvs. Q=konst. Derfor
C 1 U 1 \u003d C 2 U 2, (1)
hvor C 2 og U 2 er henholdsvis kapasitansen og potensialforskjellen på kondensatorplatene etter at de er flyttet fra hverandre.
Gitt at kapasitansen til en flat kondensator 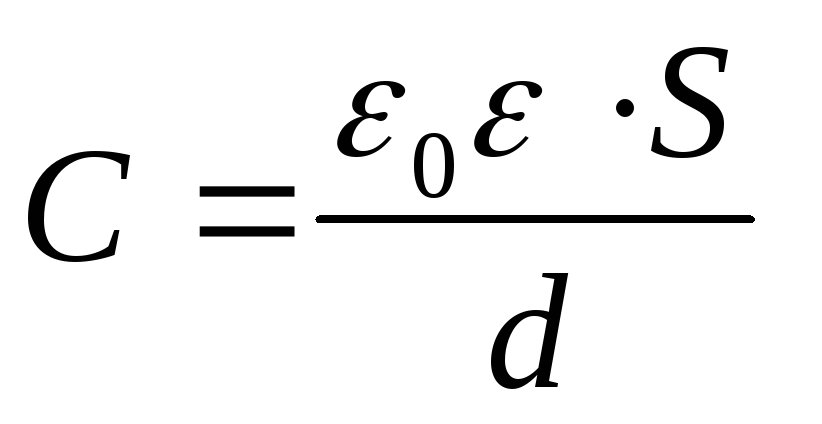 , fra formel (1) får vi den ønskede potensialforskjellen
, fra formel (1) får vi den ønskede potensialforskjellen
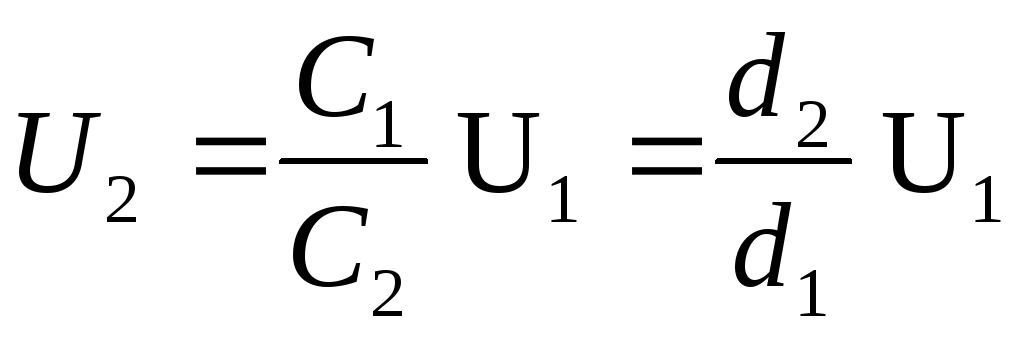 (2)
(2)
Etter å ha koblet kondensatoren fra spenningskilden, kan systemet med to ladede plater betraktes som lukket, for hvilke loven om bevaring av energi er oppfylt: arbeidet A med ytre krefter er lik endringen i systemets energi
A \u003d W 2 - W 1 (3)
hvor W 1 og W 2 er energien til kondensatorfeltet i henholdsvis start- og slutttilstand.
Gitt at 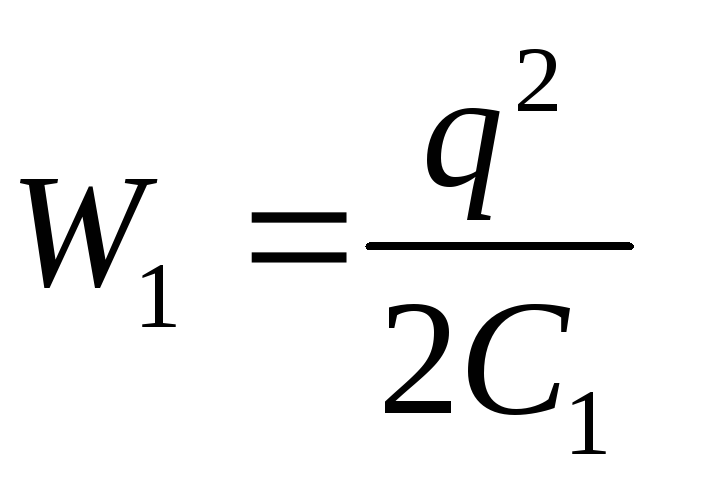 Og
Og 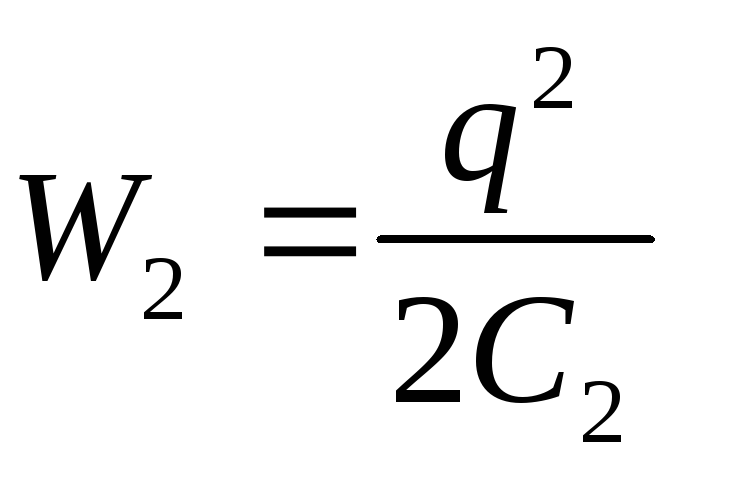 (q – const), fra formel (3) får vi ønsket arbeid av ytre krefter
(q – const), fra formel (3) får vi ønsket arbeid av ytre krefter
[tatt i betraktning at q=C 1 U 1 og formel (2)].
Svar : 1) U 2 \u003d 200V; 2) A \u003d 40nJ.
Eksempel 12.7. En solid kule av dielektrikum med en radiusR=5 cm ladet jevnt med bulktetthet ρ=5nC/m 3 . Bestem energien til det elektrostatiske feltet i rommet rundt ballen.
Gitt R=5cm=5∙10-2m; ρ=5nC/m 3 = 5∙10 -9 C / m 3.
Finne: W.
Løsning . Feltet til en ladet ball er sfærisk symmetrisk, så den volumetriske ladningstettheten er den samme på alle punkter som ligger i like avstander fra midten av ballen.
E 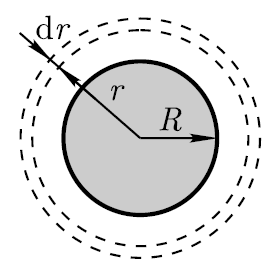 energi i et elementært sfærisk lag (det velges utenfor dielektrikumet, hvor energien skal bestemmes) med et volum på dV (se figur)
energi i et elementært sfærisk lag (det velges utenfor dielektrikumet, hvor energien skal bestemmes) med et volum på dV (se figur)
hvor dV=4πr 2 dr (r er radien til et elementært sfærisk lag; dr er dets tykkelse); 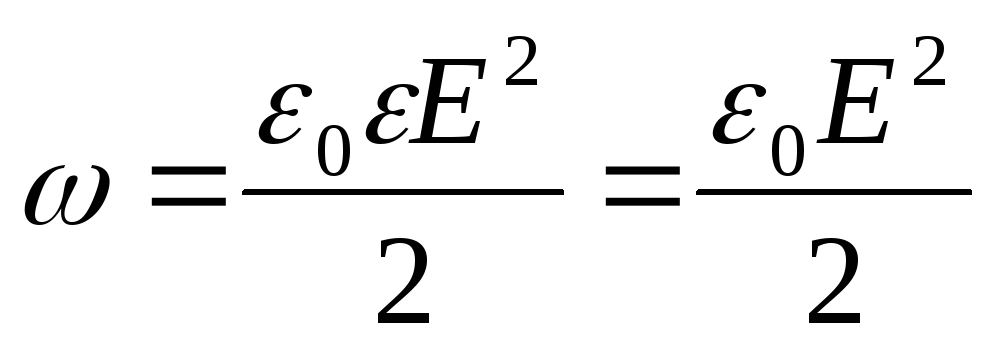 (ε=1 – felt i vakuum; E – elektrostatisk feltintensitet).
(ε=1 – felt i vakuum; E – elektrostatisk feltintensitet).
Vi vil finne intensiteten E ved Gauss-teoremet for et felt i vakuum, og mentalt velge en kule med radius r som lukket flate (se figur). I dette tilfellet kommer hele ladningen til ballen, som skaper feltet under vurdering, inn i overflaten, og ifølge Gauss-teoremet,
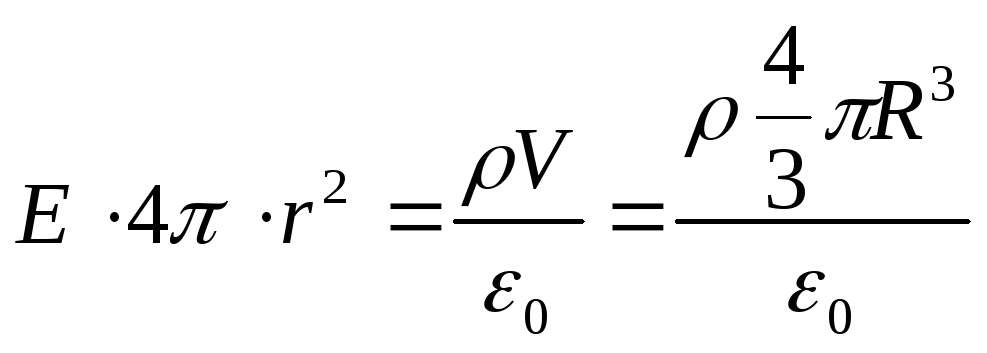
Hvor 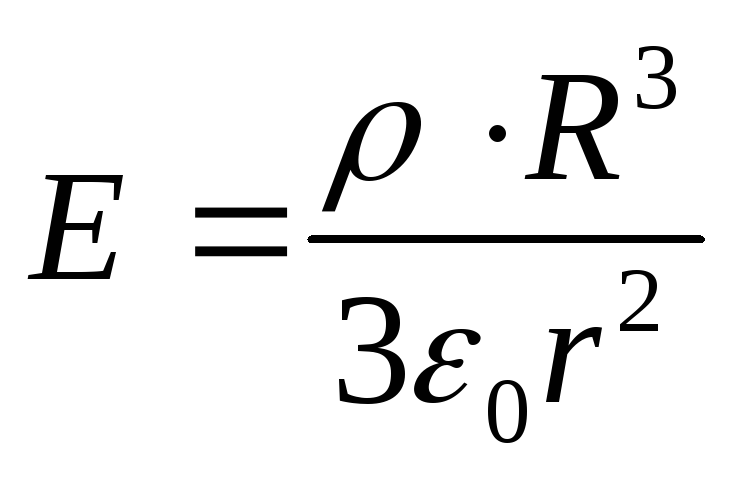
Ved å erstatte de funnet uttrykkene med formel (1), får vi
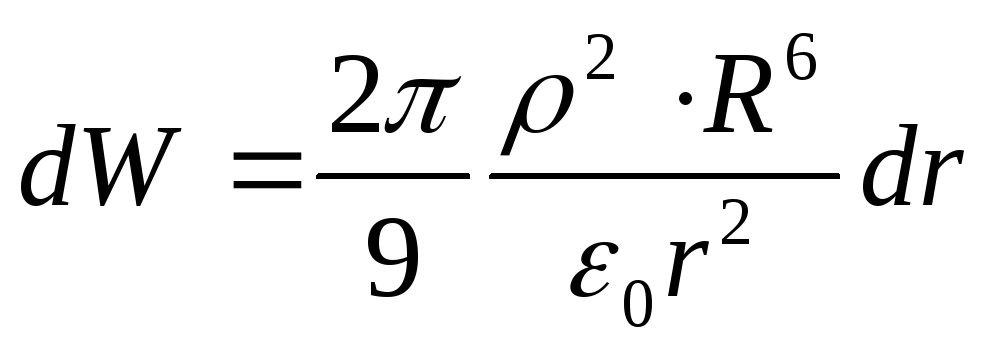
Energien som finnes i rommet rundt ballen,
Svar: B=6,16∙10 -13 J.
Eksempel 12.7. Plan kondensator med arealet til plateneSog avstanden mellom dem ℓ ladningen rapporteresq, hvoretter kondensatoren kobles fra spenningskilden. Bestem tiltrekningskraftenFmellom kondensatorplatene, dersom dielektrisitetskonstanten til mediet mellom platene er lik ε.
Gitt : S; ℓ; q; ε .
Finne: F.
Løsning . Ladningen av kondensatorplatene etter frakobling fra spenningskilden endres ikke, dvs. q=konst. Anta at under påvirkning av tiltrekningskraften F, har avstanden mellom kondensatorplatene endret seg med d ℓ . Da virker kraften F
I henhold til loven om bevaring av energi er dette arbeidet lik energitapet til kondensatoren, dvs.
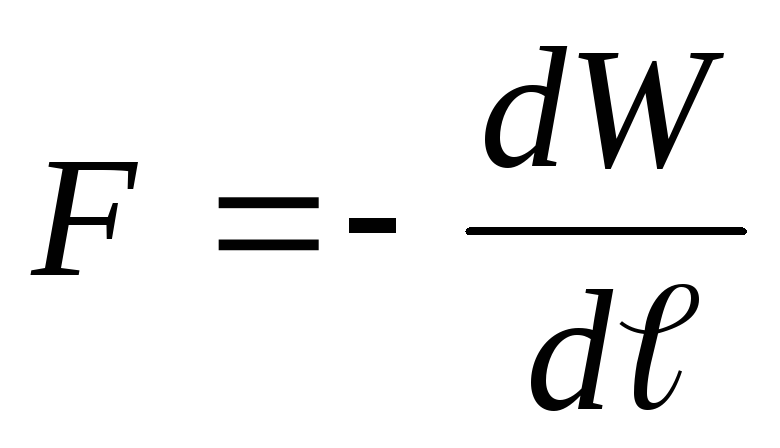 .
(3)
.
(3)
Bytter inn i formelen for energien til en ladet kondensator 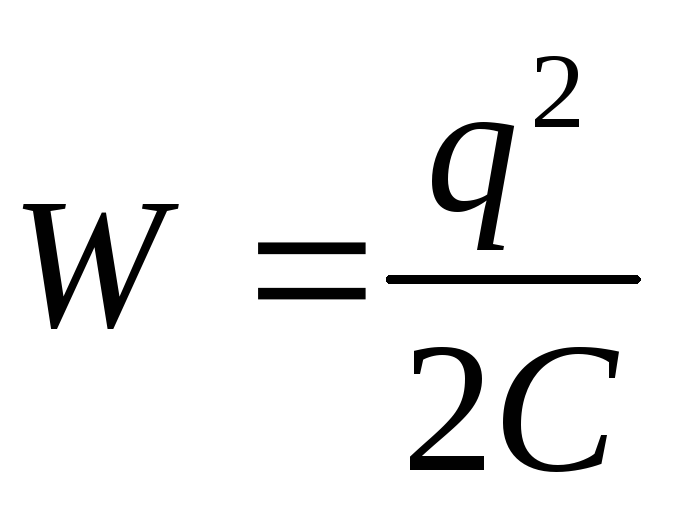 uttrykk for kapasitansen til en flat kondensator
uttrykk for kapasitansen til en flat kondensator 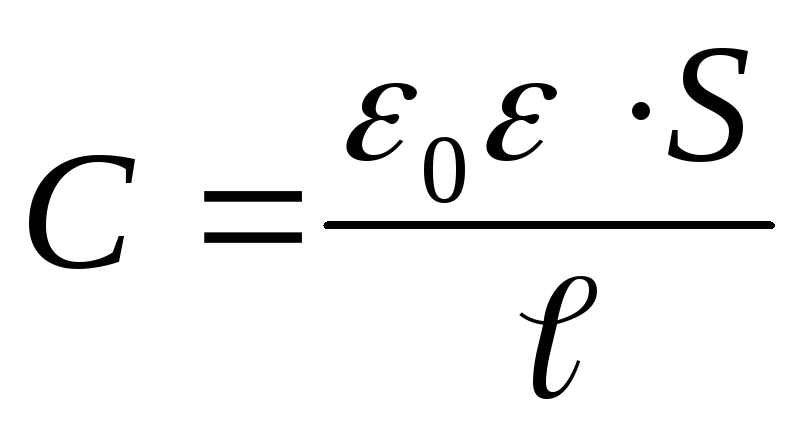 , vi får
, vi får
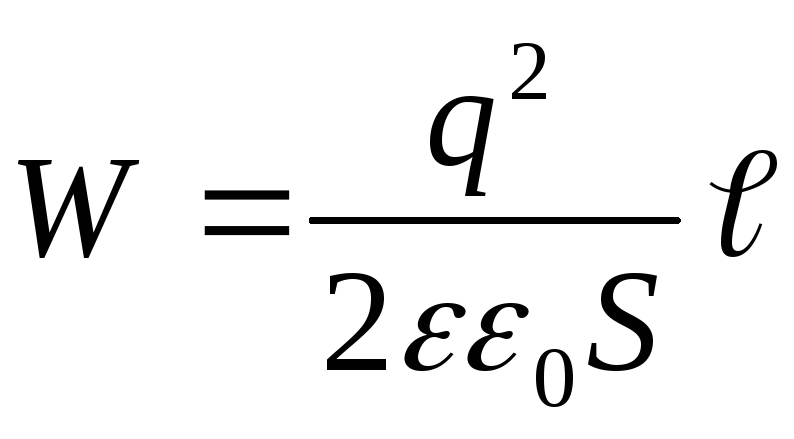 (4)
(4)
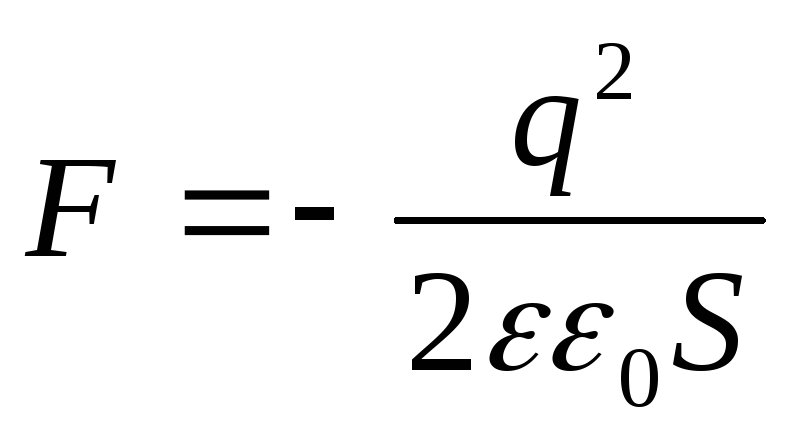
Svar:
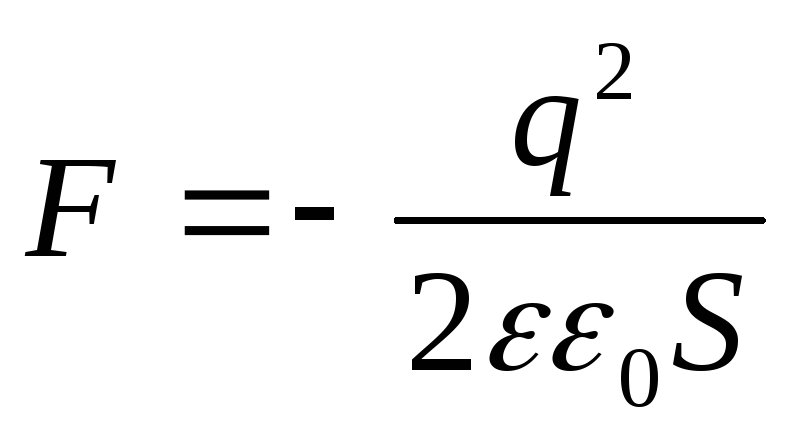
Eksempel 12.7. Flat plate kondensatorSog avstanden mellom dem ℓ koblet til en konstant spenningskildeU. Bestem tiltrekningskraftenFmellom kondensatorplatene, dersom dielektrisitetskonstanten til mediet mellom platene er lik ε.
Gitt : S; ℓ; U; ε .
Finne: F.
Løsning . I henhold til problemets tilstand opprettholdes en konstant spenning på kondensatorplatene, dvs. U=konst. Anta at under påvirkning av tiltrekningskraften F, har avstanden mellom kondensatorplatene endret seg med dℓ. Da virker kraften F
I henhold til loven om bevaring av energi går dette arbeidet i dette tilfellet til å øke energien til kondensatoren (sammenlign med forrige oppgave), dvs.
hvorfra, basert på uttrykk (1) og (2), får vi
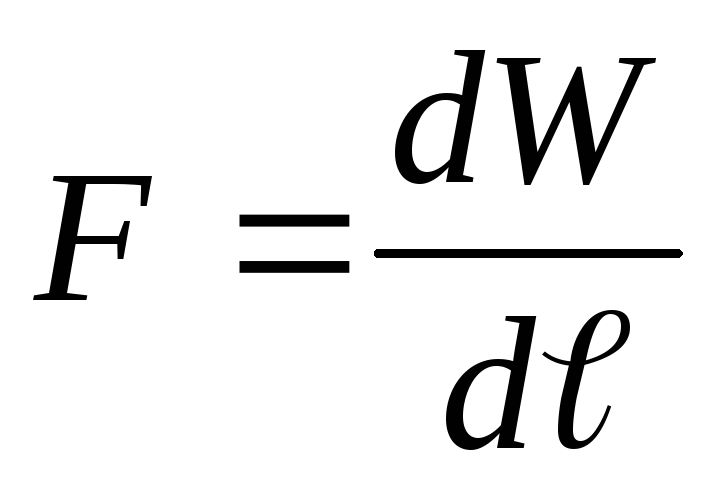 (3)
(3)
Bytter inn i formelen for energien til kondensatoren 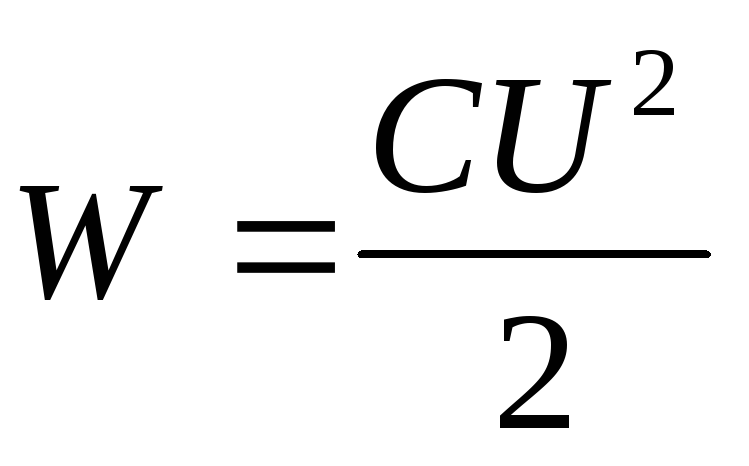 uttrykk for kapasitansen til en flat kondensator
uttrykk for kapasitansen til en flat kondensator  , vi får
, vi får
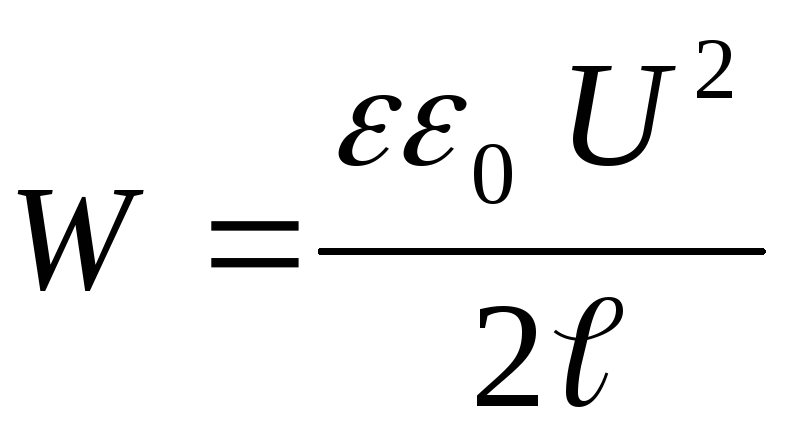 (4)
(4)
Ved å erstatte energiverdien (4) i formel (3) og utføre differensiering, finner vi ønsket tiltrekningskraft mellom kondensatorplatene
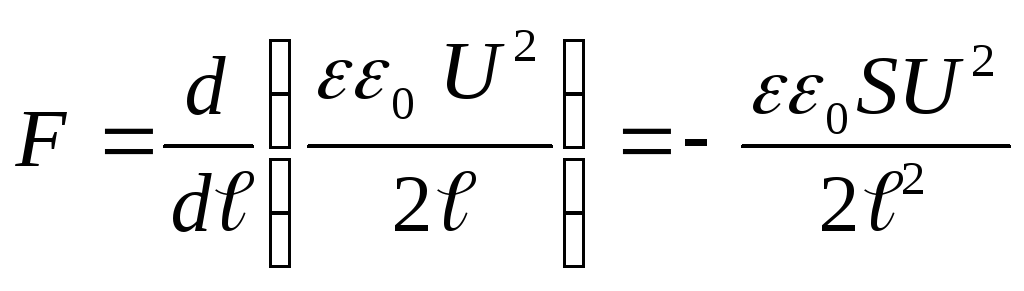 .
.
hvor "-"-tegnet indikerer at kraften F er en tiltrekningskraft.
Svar
: