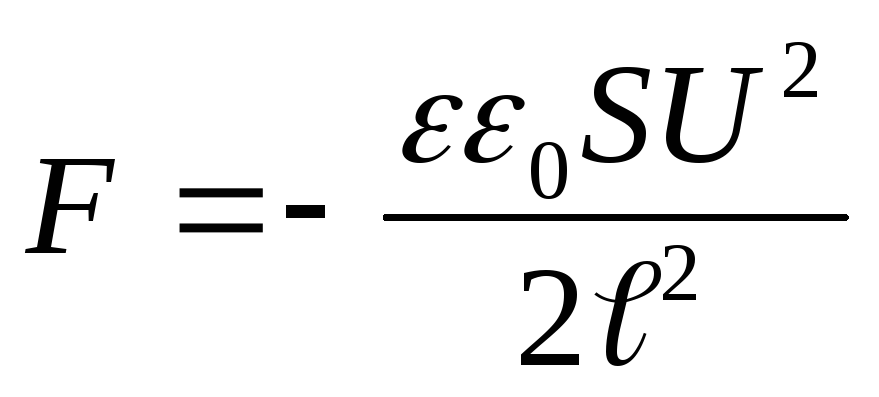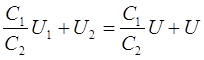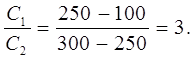Kokonaispotentiaaliero U 0 elektrodien välissä on
Laskelmat:
Vastaus: pintavarauksen tiheys kondensaattorin levyillä
Ongelma 23
Levyalue tasainen ilman lauhdutin, niiden välinen etäisyys d= 5 mm. Potentiaaliero kohdistetaan kondensaattorin levyihin. Kun kondensaattori on irrotettu jännitelähteestä, kondensaattorilevyjen välinen tila täytetään eboniitilla. Mikä on levyjen potentiaaliero täytön jälkeen? Selvitä levyjen kondensaattorin kapasitanssit ja pintavarauksen tiheydet ennen ja jälkeen täyttöä.
| d
|
| d
|
sitten ennen ja jälkeen täytön meillä on
Olettaen että s=vakio Ja d=vakio, saamme
![]()
Meillä on ennen ja jälkeen eboniittitäyttöä
![]()
Pintavaraustiheys
Laskelmat:
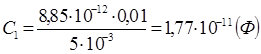
Vastaus: meillä on ennen ja jälkeen eboniittitäytön
Ongelma 24
Levyjen välissä litteä kondensaattori, joka sijaitsee etäällä d=1 cm toisistaan, käytetty potentiaaliero U\u003d 100 V. Yhden levyn vieressä on kiteisen talliumbromidin () paksuinen yhdensuuntainen levy. Kun kondensaattori on irrotettu jännitelähteestä, kidelevy poistetaan. Mikä on potentiaaliero kondensaattorin levyjen välillä tämän jälkeen?
voimme kirjoittaa
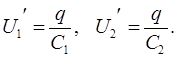
Akun jännite on yhtä suuri kuin yksittäisten kondensaattoreiden jännitteiden summa, ts.
![]()
Siten,
Siksi kapasiteetin vuoksi KANSSA koko löytämämme akusta
| KANSSA -q + q d0 e e 01 U 1 |
| С¢ d +q -q e=1 U 2 |
Korvaamalla (1) luvulla (2), saamme
Kondensaattorin kapasitanssi toisessa asennossa
Varauksen säilymislain mukaan q=q¢, eli
Laskelmat:
Vastaus: potentiaalieroksi tulee 1,8 kV.
Ongelma 25
Etsi kapasiteetti KANSSA kuvassa näkyvä kondensaattorijärjestelmä. Jokaisen kondensaattorin kapasitanssi KANSSA\u003d 0,5 uF.
| C1 C3 C2 |
löytö C res tuloksena oleva kondensaattoripankki.
Harkitse akkua ja kondensaattoria Alkaen 3, ne on kytketty sarjaan. Tietäen, että klo sarjaliitäntä
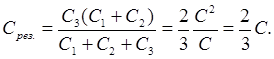
Laskelmat:
Vastaus: kondensaattorijärjestelmän kapasitanssi on uF.
Ongelma 26
Kahden kondensaattorin kapasitanssia verrattiin elektrometriin. Tätä varten heitä veloitettiin mahdollisista eroista U 1= 300 V ja U 2= 100 V ja kytketty molemmat kondensaattorit rinnan. Tässä tapauksessa kondensaattorilevyjen välillä mitattu potentiaaliero osoittautui yhtä suureksi U\u003d 250 V. Selvitä kapasiteettien suhde
| A) C1 + - U 1 |
| b) C2
Missä U- potentiaaliero levyjen välillä niiden liittämisen jälkeen.
Arvojen korvaaminen q 1, q 2, q 1 ¢, q 2 ¢ lausekkeeksi (1), saamme jaettuna KANSSA 2
Laskelmat:
Vastaus: kondensaattorien suhde Ongelma 27 Litteän kondensaattorin levyt, joissa on alue Korvaa (2) kohtaan (1) ja ilmaista q Korvaamme lausekkeen (2) lausekkeella (4), saamme Korvaa (5) osaksi (6) Laskelmat: |
Lukukausi 3. Luento4.
Luento 4. Varautuneiden johtimien sähkökenttä.
Sähköstaattisen kentän energia.
Kenttä lähellä johdinta. Johtimien ja kondensaattorien kapasitanssi. (Litteiden, sylinterimäisten ja pallomaisten kondensaattorien kapasiteetit). Kiinteiden maksujen järjestelmän energia. Varautuneen johtimen, kondensaattorin energia. Sähköstaattisen kentän energiatiheys.
Kun johdin viedään ulkoiseen sähkökenttään, johtimen sisällä olevat varaukset alkavat liikkua ulkoisesta kentästä tulevien voimien vaikutuksesta, kunnes tasapaino saavutetaan. Tämä johtaa sähkövarauksen uudelleen jakautumiseen johtimen sisällä. Aiemmin sähköisesti neutraalit johtimen alueet saavat kompensoimattoman sähkövarauksen. Tämän seurauksena sähkökenttä ilmestyy (tai, kuten sanotaan, indusoituu) johtimeen 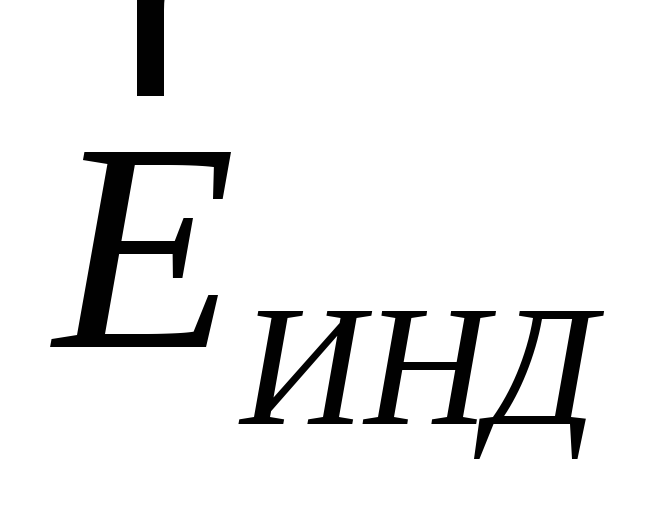 . Sähkövarausten tasapainon ehto:
. Sähkövarausten tasapainon ehto:
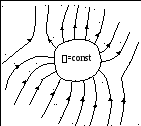 ,
,
nuo. kentänvoimakkuus johtimen sisällä:
Siksi saamme tasa-arvosta ![]() johtimen sisällä. Siksi tämä ehto täyttyy myös johtimen rajalla. Nuo. johtimen pinta on ekvipotentiaali
pinta
, Siksi voimalinjat sähkökenttä kohtisuorassa johtimen pintaan nähden kussakin pisteessä
.
johtimen sisällä. Siksi tämä ehto täyttyy myös johtimen rajalla. Nuo. johtimen pinta on ekvipotentiaali
pinta
, Siksi voimalinjat sähkökenttä kohtisuorassa johtimen pintaan nähden kussakin pisteessä
.
ladattu johdin .
Jos yksittäiseen johtimeen välitetään ulkoinen sähkövaraus, niin varausten tasapainon ehto johtaa jälleen ehtoon:
,![]() johtimen sisällä.
johtimen sisällä.
Tästä seuraa, että kaikki ulkoiset varaukset sijaitsevat johtimen pinnalla, koska. kentänvoimakkuus johtimen sisällä on nolla, ja Gaussin lauseen mukaan mille tahansa johtimen sisällä olevalle suljetulle pinnalle (mukaan lukien johtimen ulkopinta):
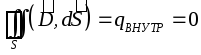 .
.
Koska tässä tapauksessa johtimen pinta on myös ekvipotentiaalinen, sähkökentän voimalinjat suunnataan kohtisuoraan johtimen pintaan nähden sen jokaisessa pisteessä.
Gaussin lauseesta seuraa, että lähellä johtimen pintaa
Sähkösiirtymävektorin suuruus on yhtä suuri kuin ulkoisten varausten pintatiheys.
Varaus johtimen pinnalla jakautuu siten, että pintapotentiaali pysyy vakiona. Tämä johtaa siihen, että varaustiheys johtimen pinnalla ei ole sama. Esimerkiksi johtimien terävissä osissa varaustiheys on suurempi kuin syvennyksissä. Tässä suhteessa syntyy erilaisia ilmiöitä, esimerkiksi "latauksen tyhjeneminen". Jos johdin on ilmassa, ilman ionisaatio tapahtuu kärjen lähellä ja kuljettaa pois osan sähkövarauksesta - ilmiö, jota kutsutaan "sähkökuuliksi".
Sähköinen kuvantamismenetelmä .
Jos ekvipotentiaalipinta korvataan johtavalla, ja tämän pinnan erottama kentän osa hylätään, kenttäkuvio ei muussa osassa muutu. Päinvastoin, jos kenttäkuvaa täydennetään kuvitteellisilla varauksilla siten, että johtava pinta voidaan korvata potentiaalintasaisella, alkuperäinen kenttäkuva ei muutu.
Esimerkki.Etsi pistevarauksen vetovoima äärettömään johtavaan tasoon
. Tätä varten täydennämme kuvaa toisella samantyyppisellä, mutta vastakkaisen merkin varauksella, joka sijaitsee symmetrisesti tasoon nähden. Silloin taso osuu ekvipotentiaalipinnan kanssa, joten taso voidaan hylätä ja varausten välinen vuorovaikutusvoima voidaan löytää: 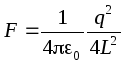 .
.
Varautuneen johtimen energia .
Yksittäisen varautuneen johtimen energia määritellään varausjärjestelmän energiaksi: 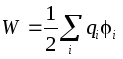 . Johtimessa, joten yksinäisen johtimen energia:
. Johtimessa, joten yksinäisen johtimen energia:
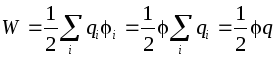 .
.
Varattujen johtimien järjestelmälle: 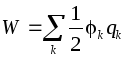 .
.
Erityisesti kahdelle johtimelle, joiden varaukset q ovat samansuuruisia, mutta eri etumerkillä, energia on yhtä suuri: 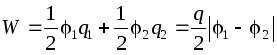 .
.
Kommentti
. Potentiaalieron suuruus ![]() nimeltään Jännite
ruumiiden välillä.
nimeltään Jännite
ruumiiden välillä.
Kokemus osoittaa, että yksittäisen johtimen varauksen ja sen potentiaalin välillä on lineaarinen suhde: . Suhteellisuustekijä KANSSA nimeltään sähkökerroin
astiat tai sähköinen kapasiteetti
.
Sähkökapasiteetin yksikkö on Farad ( 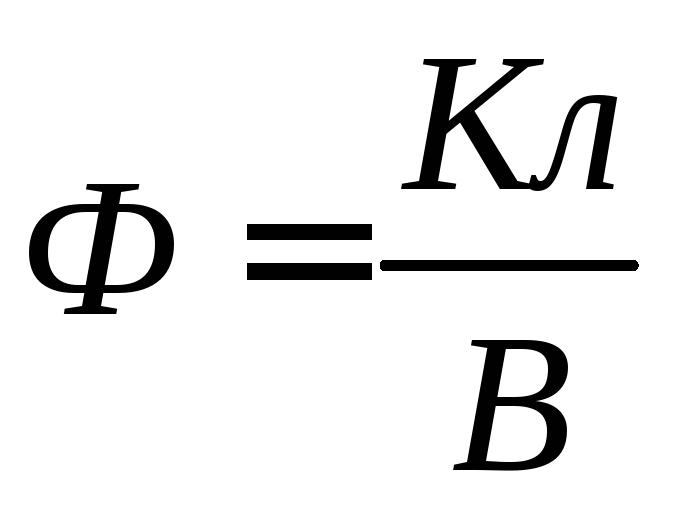 ).
).
Kondensaattori Sitä kutsutaan kahden johtimen järjestelmäksi, jotka on varattu samalla suuruudella, mutta eri etumerkillä. Johtimet kutsutaan kondensaattorilevyt .
Kondensaattorin kapasitanssi määräytyy kaavan mukaan.
Kondensaattori on perinteisesti merkitty.
Kondensaattorien kytkentä
Harkitse kahden kondensaattorin C 1 ja C 2 sarjakytkentää. Kondensaattorien välinen piste A on erotettu muusta piiristä, joten sen sähkövaraus ei voi muuttua. Koska minkä tahansa pisteen alkuvaraus oli nolla, niin ![]() . Näin ollen pisteen A vieressä olevien kondensaattorilevyjen varaukset ovat suuruudeltaan yhtä suuret, mutta etumerkillisesti vastakkaiset. Mutta koska levyjen varauksen arvo on yhtä suuri kuin kondensaattorien varaus, niin. Pisteen A kokonaisvaraus on nolla, joten jos hylkäämme tämän pisteen yhdessä levyjen kanssa, mikään ei muutu piirissä. Koska äärilevyjen varaukset ovat myös suuruudeltaan samat, mutta eri etumerkillä, niin tuloksena olevalla kondensaattorilla on sama varaus suuruudeltaan.
. Näin ollen pisteen A vieressä olevien kondensaattorilevyjen varaukset ovat suuruudeltaan yhtä suuret, mutta etumerkillisesti vastakkaiset. Mutta koska levyjen varauksen arvo on yhtä suuri kuin kondensaattorien varaus, niin. Pisteen A kokonaisvaraus on nolla, joten jos hylkäämme tämän pisteen yhdessä levyjen kanssa, mikään ei muutu piirissä. Koska äärilevyjen varaukset ovat myös suuruudeltaan samat, mutta eri etumerkillä, niin tuloksena olevalla kondensaattorilla on sama varaus suuruudeltaan.
KAIKKI YHTEENSÄ . Sarjaan kytkettyjen kondensaattorien varaukset ovat suuruudeltaan samat. Sarjaan kytkettyjen kondensaattorien kokonaisvaraus on yhtä suuri kuin kunkin kondensaattorin varaus.
Tässä tapauksessa kokonaisjännite on yhtä suuri kuin kondensaattoreiden jännitteiden summa: U YLEINEN \u003d U 1 + U 2. Kondensaattorien varaukset ovat samat: q 1 \u003d q 2 \u003d q. Sitten 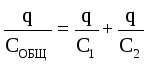 . Siksi
. Siksi 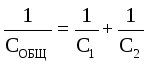 .
.
Kun kondensaattorit kytketään sarjaan, niiden kapasitanssit lisätään käänteislain mukaan .
Kapasitanssilaskenta kondensaattoreiden rinnakkaiskytkentää varten.
Tässä tapauksessa kondensaattoreiden jännitteet ovat samat: U 1 \u003d U 2 \u003d U.
Kokonaisvaraus on yhtä suuri kuin varausten summa: q GEN = q 1 + q 2 tai C GEN U=C 1 U+C 2 U.
Sitten C YLEISTÄ =C 1 +C 2 . Kun kondensaattorit kytketään rinnan, niiden kapasitanssit kasvavat.
Kondensaattorin energia :
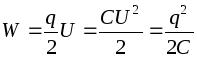 .
.
Kondensaattorin kokonaisvaraus on nolla. Kondensaattori varastoi sähköenergiaa erottamalla sähkövaraukset.
Esimerkkejä kondensaattoreiden kapasitanssin laskemisesta .
Tasainen (ilma) lauhdutin tarkoittaa kahta yhdensuuntaista levyä, joiden välinen etäisyys on paljon pienempi kuin levyjen mitat, joten levyjen välistä kenttää voidaan pitää yhtenäisenä. Levyjen välissä on tyhjiö (ilma), joten = 1.
 Tässä tapauksessa kenttäkuviota laskettaessa voidaan käyttää äärettömän varautuneen tason kentälle saatuja tuloksia. Koska levyjen varaukset ja pinta-alat ovat suuruudeltaan yhtä suuret, kunkin levyn luoman kentänvoimakkuuden suuruus on sama: mutta intensiteettivektorien suunnat ovat erilaiset (intensiteettivektori negatiivisesti varautuneesta levystä on esitetty katkoviiva). Levyjen välillä intensiteettivektorit suunnataan samalla tavalla, joten kokonaisintensiteetti on yhtä suuri kuin kunkin levyn luomien kenttävoimakkuuksien summa:
Tässä tapauksessa kenttäkuviota laskettaessa voidaan käyttää äärettömän varautuneen tason kentälle saatuja tuloksia. Koska levyjen varaukset ja pinta-alat ovat suuruudeltaan yhtä suuret, kunkin levyn luoman kentänvoimakkuuden suuruus on sama: mutta intensiteettivektorien suunnat ovat erilaiset (intensiteettivektori negatiivisesti varautuneesta levystä on esitetty katkoviiva). Levyjen välillä intensiteettivektorit suunnataan samalla tavalla, joten kokonaisintensiteetti on yhtä suuri kuin kunkin levyn luomien kenttävoimakkuuksien summa:
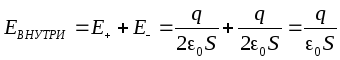 .
.
Levyjen ulkopuolella kentänvoimakkuusvektorit on suunnattu vastakkain, joten kentänvoimakkuus ulkopuolella on nolla. Täten, kondensaattorissa kentänvoimakkuus on nollasta poikkeava vain levyjen välillä.
Koska sähköstaattinen kenttä on konservatiivisen voiman kenttä, integraali 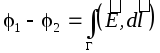 ei riipu liikeradan muodosta G, joten levyjen välinen potentiaaliero löytyy levyjä yhdistävää kohtisuoraa pitkin, jonka pituus on yhtä suuri kuin d:
ei riipu liikeradan muodosta G, joten levyjen välinen potentiaaliero löytyy levyjä yhdistävää kohtisuoraa pitkin, jonka pituus on yhtä suuri kuin d: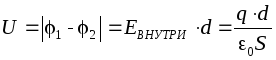 , Missä d on levyjen välinen etäisyys. Sitten määritelmän mukainen litteän (ilma)kondensaattorin kapasitanssi on yhtä suuri:
, Missä d on levyjen välinen etäisyys. Sitten määritelmän mukainen litteän (ilma)kondensaattorin kapasitanssi on yhtä suuri: 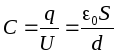
Sylinterimäinen (ilma) lauhdutin koostuu kahdesta koaksiaalisylinteristä
samanpituisia, sisäkkäisiä toisiinsa siten, että levyjen välinen etäisyys on paljon pienempi kuin levyjen mitat.
Anna kondensaattorin pituus L, sisävuorauksen varaus on positiivinen: q > 0. Pinnoitussäteet R 1 ja R 2, anna R 1 <R 2. Kentänvoimakkuus levyjen välillä etäisyyden päässä r sisävuorauksesta, ts. varten R 1 <r <R 2, löydämme Gaussin lauseen avulla:
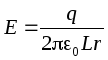 .
.
Sitten levyjen välinen jännite: .
Siksi sylinterimäisen (ilma)kondensaattorin sähköinen kapasiteetti: ![]() .
.
KANSSA  pallomainen (ilma) lauhdutin
edustaa kahta sisäkkäistä samankeskistä palloa levyjen säteiden kanssa R 1 ja R 2 ,R 1 <R 2. Olkoon sisävuorauksen varaus q> 0. Kentänvoimakkuus vuorausten välillä etäisyyden päässä r sisävuoresta ( R 1
<r
<R 2) löydämme Gaussin lauseen avulla:
pallomainen (ilma) lauhdutin
edustaa kahta sisäkkäistä samankeskistä palloa levyjen säteiden kanssa R 1 ja R 2 ,R 1 <R 2. Olkoon sisävuorauksen varaus q> 0. Kentänvoimakkuus vuorausten välillä etäisyyden päässä r sisävuoresta ( R 1
<r
<R 2) löydämme Gaussin lauseen avulla:
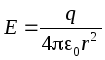 .
.
Levyjen välinen jännitys: .
Siksi pallomaisen (ilma)kondensaattorin kapasitanssi ![]() .
.
Sähköstaattisen kentän tilavuusenergiatiheys.
Harkitse tasaista ilmalauhdutinta. Ladatun kondensaattorin energia
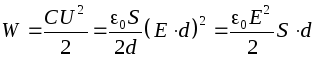 .
.
Kondensaattorin levyjen välisen tilan määrä. Koska levyjen välisen kentän katsotaan olevan homogeeninen, tämän kentän tilavuusyksikkö on energia 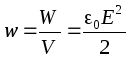 . Tätä arvoa kutsutaan tilavuusenergiatiheys
.
. Tätä arvoa kutsutaan tilavuusenergiatiheys
.
Siinä tapauksessa, että kenttä ei ole tasainen, tilavuusenergiatiheys on .
Aineessa sähkökentän tilavuusenergiatiheys 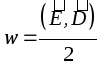 .
.
Homogeenisen isotrooppisen dielektrisen aineen tapauksessa 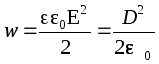 .
.
Koska ![]() , Tuo
, Tuo 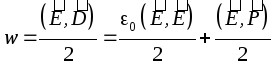 , Missä
, Missä
Sähkökentän energia tyhjiössä on aineen polarisaation energiaa.
Esimerkki . Tarkastellaan varautunutta ohutseinäistä palloa, jonka säde on R. Koska samannimiset varaukset hylkivät toisiaan pallolla, hylkivillä voimilla on taipumus venyttää pallon pintaa. Voimme olettaa, että pallon sisältä seiniin vaikuttaa lisäpaine p, halkeaa pallon ja aiheutuu pinnalla olevasta sähkövarauksesta. Etsitään R.
Kentänvoimakkuus pallon sisällä on nolla, joten sähkökentän tilavuusenergiatiheys w eroaa nollasta vain pallon ulkopuolella.
Pallon säteen lievä lisäys DR sen tilavuus kasvaa, kun taas siinä ympäröivän tilan osassa, joka joutui pallon sisälle, tilavuusenergiatiheys tulee nollaksi. Siksi ulkoisen kentän energian muutos on yhtä suuri kuin missä S on pinta-ala. Mutta pallon laajentuessa pallon sisällä olevat painevoimat tekevät työn ![]() . Siitä lähtien
. Siitä lähtien ![]() mistä.
mistä.
Esimerkki . Etsitään levyihin vaikuttavat voimat ladatussa litteässä kondensaattorissa, joka on irrotettu virtalähteestä.
Levyt ovat vastakkaisesti varattuja, joten ne houkuttelevat. Oletetaan, että levyt ovat lähellä toisiaan vähän. x. Sitten lauhduttimen tilavuus pienenee dV = xS, joten kondensaattorin energia on pienentynyt dW = wdV. Houkuttelevat voimat toimivat A = fx. Koska A= dW, Tuo fx = wxS. Siksi voiman suuruus on F = wS. Näiden voimien aiheuttama lisäpaine on yhtä suuri kuin.
Yllä olevat esimerkit osoittavat, että sähkökentässä oleviin kappaleisiin kohdistuu voimia, jotka aiheuttavat tilavuusenergiatiheyttä vastaavan lisäpaineen.
Sähkökentän olemassaolon aiheuttama paine on yhtä suuri kuin tilavuusenergiatiheys .
Voimat , vaikuttaa vartaloon jonkin kentän puolelta, kutsutaan pondemotoriksi .
Vastakkaisesti varautuneet kondensaattorilevyt vetävät toisiaan puoleensa.
Makroskooppisiin varautuneisiin kappaleisiin vaikuttavia mekaanisia voimia kutsutaanpohdiskelua .
Laskemme tasaisen kondensaattorin levyihin vaikuttavat ponderomotoriset voimat. Tässä tapauksessa kaksi vaihtoehtoa on mahdollista:
Kondensaattori on ladattu ja irrotettu ladatusta akusta(tässä tapauksessa levyjen varausten määrä pysyy vakiona q = konst).
Kun kondensaattorin toinen levy poistetaan toisesta, työ on tehty
jonka vuoksi järjestelmän potentiaalienergia kasvaa:
Tässä tapauksessa dA = dW. Yhdistämällä näiden lausekkeiden oikeat puolet saadaan
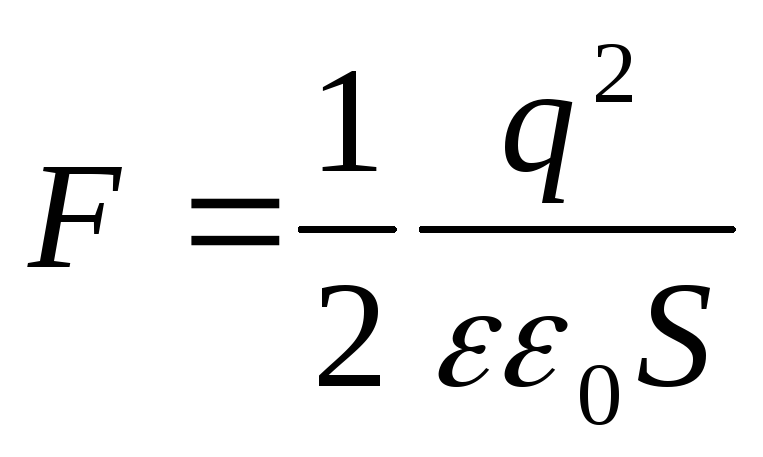 (12.67)
(12.67)
Tässä tapauksessa erotettaessa levyjen välinen etäisyys merkittiin x.
Kondensaattori ladattu, mutta ei irrotettu akusta(tässä tapauksessa siirrettäessä yhtä kondensaattorilevyistä jännite pysyy vakiona ( U = konst). Tässä tapauksessa, kun yksi levy siirtyy pois toisesta, kondensaattorikentän potentiaalienergia pienenee, koska varaukset "vuotavat" levyistä, joten
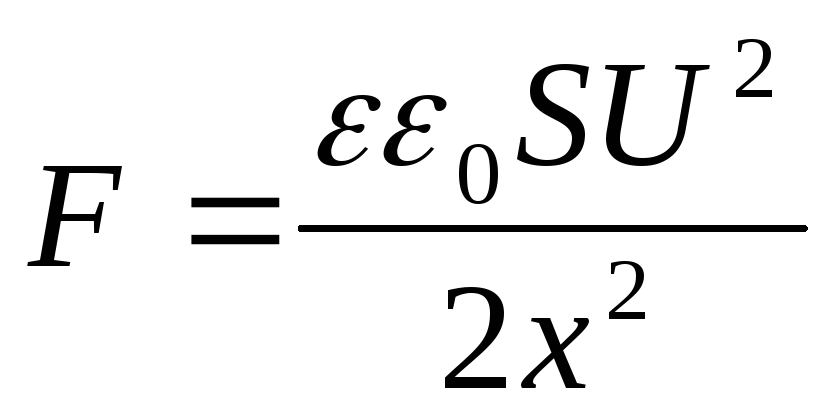
Mutta 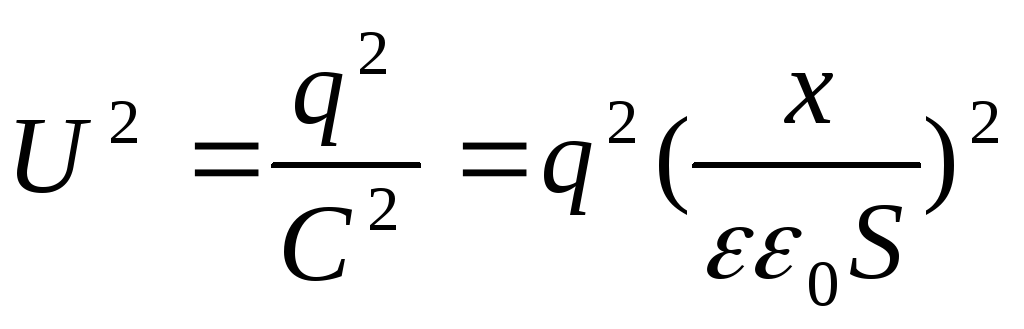 , Sitten
, Sitten
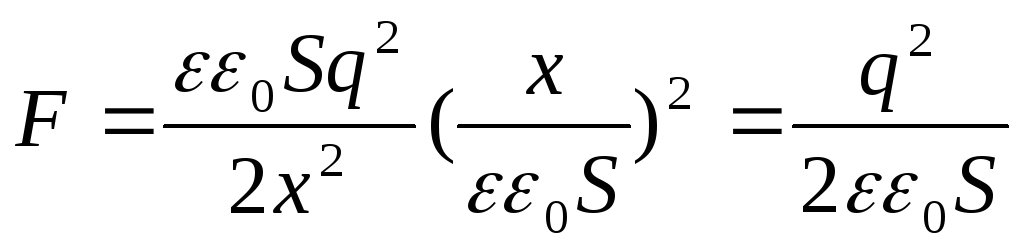
Tuloksena oleva lauseke osuu yhteen kaavan kanssa 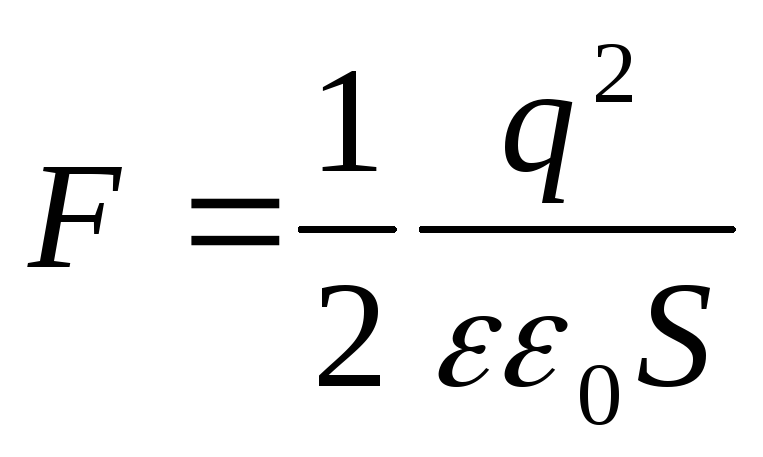 . Se voidaan esittää myös toisessa muodossa, jos varauksen q sijasta otetaan käyttöön pintatiheys:
. Se voidaan esittää myös toisessa muodossa, jos varauksen q sijasta otetaan käyttöön pintatiheys:
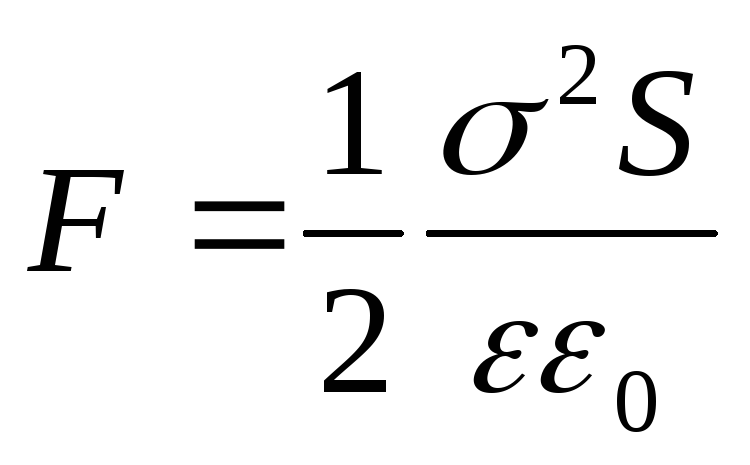 (12.68)
(12.68)
Kenttä on yhtenäinen. Kondensaattorin kentänvoimakkuus on 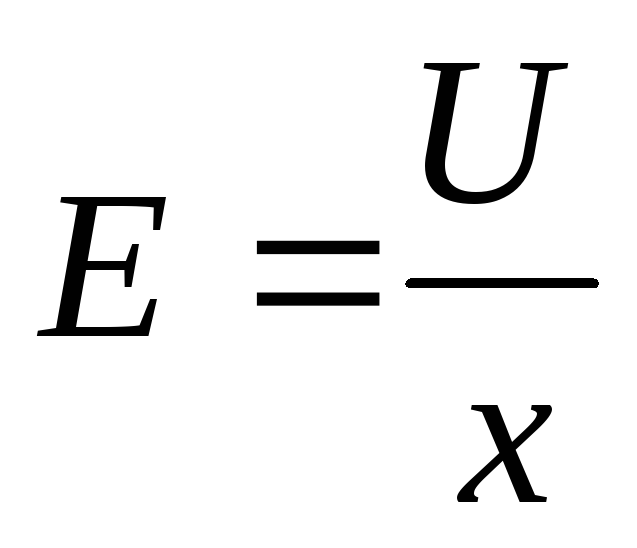 , missä x on levyjen välinen etäisyys. Korvaaminen kaavaan
, missä x on levyjen välinen etäisyys. Korvaaminen kaavaan 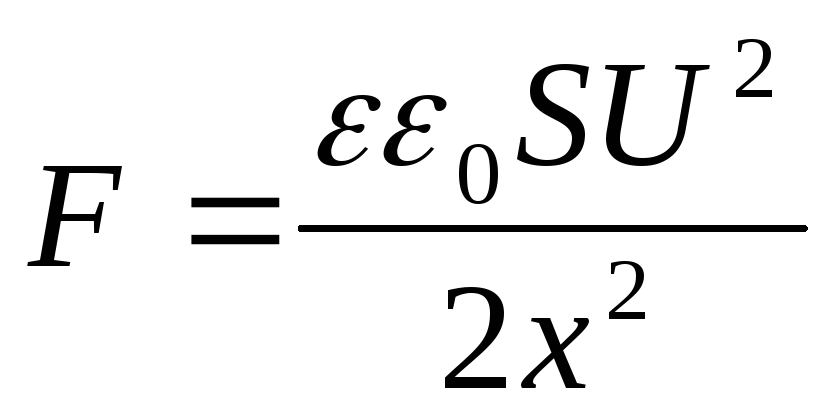 U 2 \u003d E 2 x 2, saamme, että litteän kondensaattorin levyjen vetovoima
U 2 \u003d E 2 x 2, saamme, että litteän kondensaattorin levyjen vetovoima
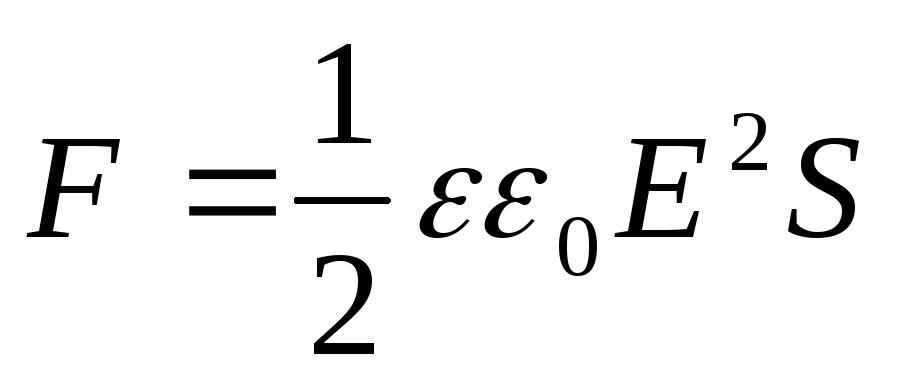 (12.69)
(12.69)
Nämä voimat eivät vaikuta vain levyihin. Koska levyt puolestaan kohdistavat painetta niiden väliin asetettuun eristeeseen ja muuttavat sitä, syntyy painetta eristeessä
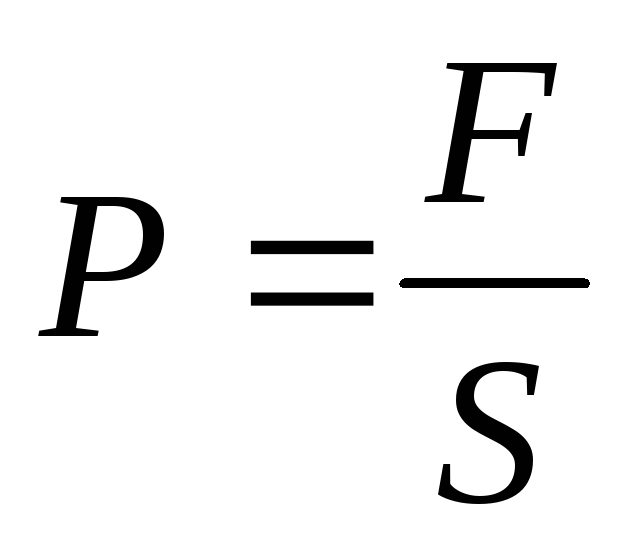
(S on jokaisen levyn pinta-ala).
Dielektrissä oleva paine on
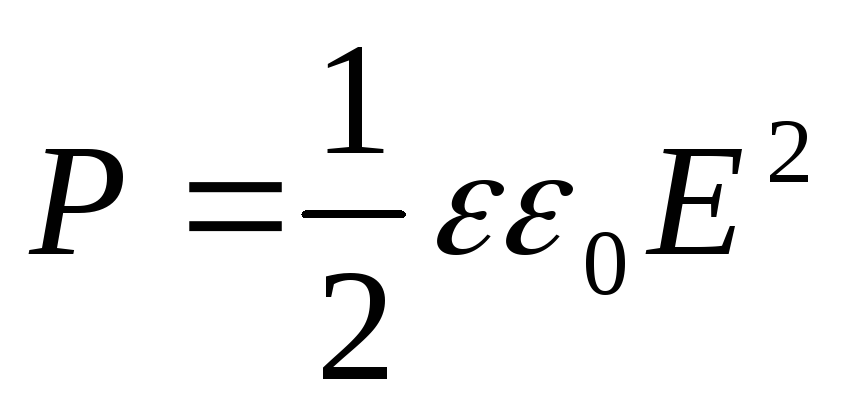 (12.70)
(12.70)
Esimerkkejä ongelmanratkaisusta
Esimerkki 12.5. Tasaisen ilmakondensaattorin levyihin kohdistetaan 1,5 kV potentiaaliero. Levyn ala 150 cm 2 ja niiden välinen etäisyys on 5 mm. Kun kondensaattori oli irrotettu jännitelähteestä, lasi asetettiin levyjen väliseen tilaan (ε 2 =7). Määrittele:
1) levyjen välinen potentiaaliero dielektrisen lisäyksen jälkeen; 2) kondensaattorin kapasitanssi ennen ja jälkeen dielektrisen asennuksen; 3) levyjen pintavarauksen tiheys ennen ja jälkeen eristeen lisäämisen.
Annettu: U 1 \u003d 1,5 kV \u003d 1,5 ∙ 10 3 V; S \u003d 150 cm 2 \u003d 1,5 ∙ 10 -2 m 2; e 1 = 1; d=5mm=5∙10 -3 m.
Etsi: 1) U2; 2) C1C2; 3) σ 1 , σ 2
Ratkaisu
.
Koska 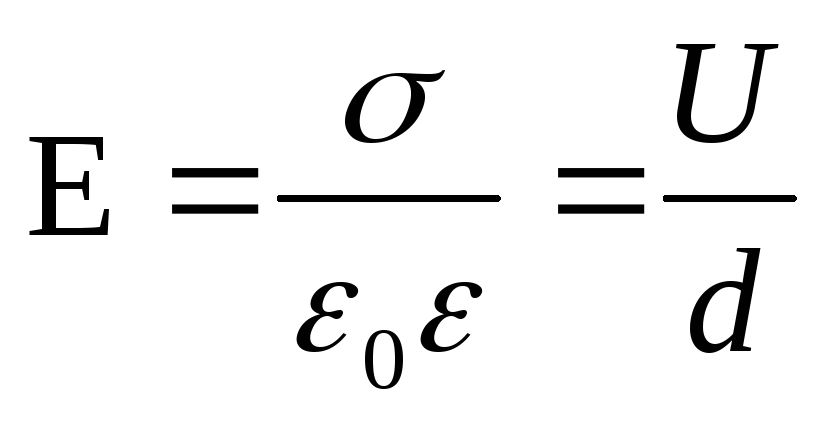 (σ on kondensaattorilevyjen pintavaraustiheys), sitten ennen eristeen lisäämistä σd=U 1 ε 0 ε 1 ja eristeen lisäämisen jälkeen σd=U 2 ε 0 ε 2, joten
(σ on kondensaattorilevyjen pintavaraustiheys), sitten ennen eristeen lisäämistä σd=U 1 ε 0 ε 1 ja eristeen lisäämisen jälkeen σd=U 2 ε 0 ε 2, joten
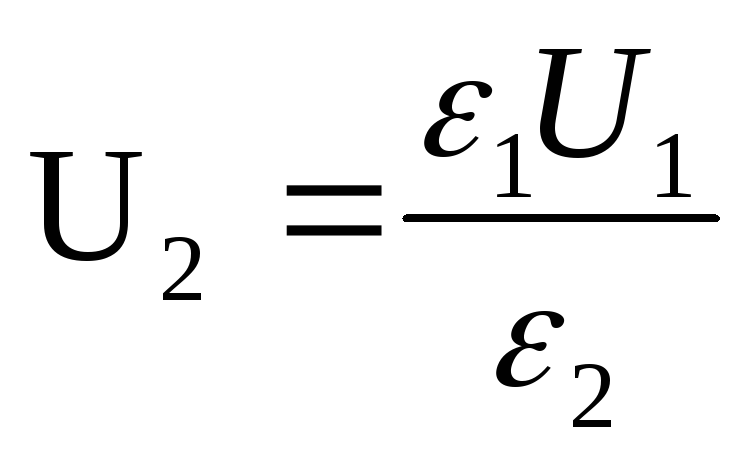
Kondensaattorin kapasitanssi ennen ja jälkeen dielektrisen käyttöönoton
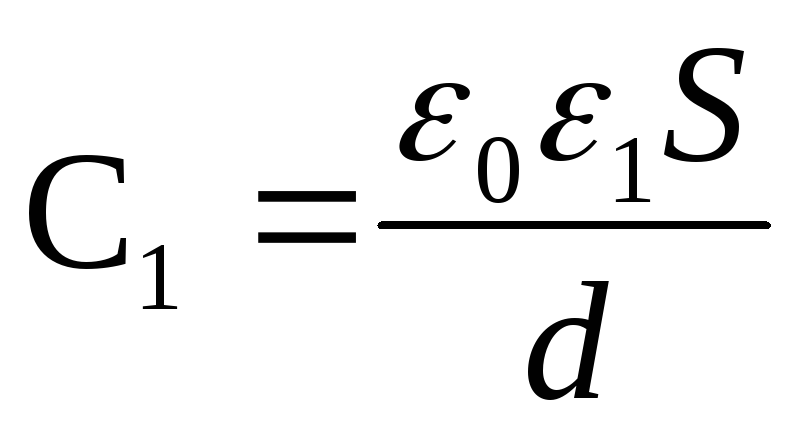 Ja
Ja 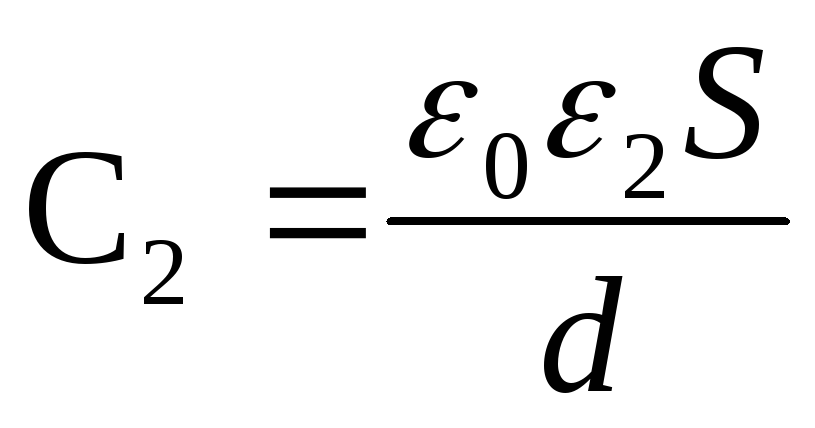
Levyjen varaus jännitelähteestä irrotuksen jälkeen ei muutu, ts. q=vakio. Siksi levyjen pintavarauksen tiheys ennen ja jälkeen dielektrisen käyttöönoton
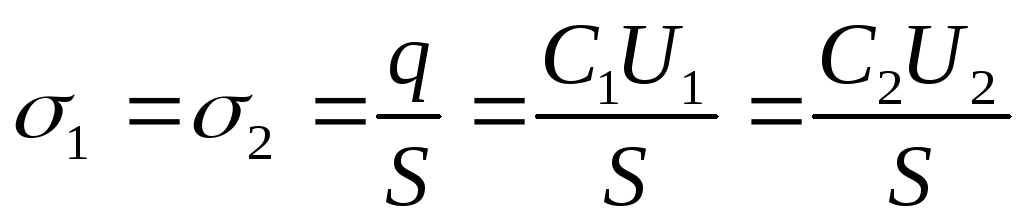
Vastaus: 1) U 2 \u003d 214V; 2) C1 \u003d 26,5 pF; C2 \u003d 186pF; 3) σ 1 = σ 2 = 2,65 μC/m 2.
Esimerkki 12.7. Tasaisen kondensaattorin levyjen välinen rako täytetään anisotrooppisella dielektrillä, jonka läpäisevyys ε vaihtelee levyihin nähden kohtisuorassa suunnassa lineaarisen lain mukaan.ε = α + βх alkaen ε 1 ε asti 2 , ja ε 2 > ε 1 . Jokaisen vuorauksen pinta-alaS, niiden välinen etäisyysd. Selvitä kondensaattorin kapasitanssi.
Annettu:S; d; e 1; ε 2
Löytö: KANSSA.
Ratkaisu
.
Dielektrisyysvakio ε
vaihtelee lineaarisesti, ε = α + βx, missä x mitataan vuorauksesta, jonka läpäisevyys on yhtä suuri kuin ε 1 . Ottaen huomioon, että ε (0) = ε 1, ε (d) = ε 2, saadaan riippuvuus 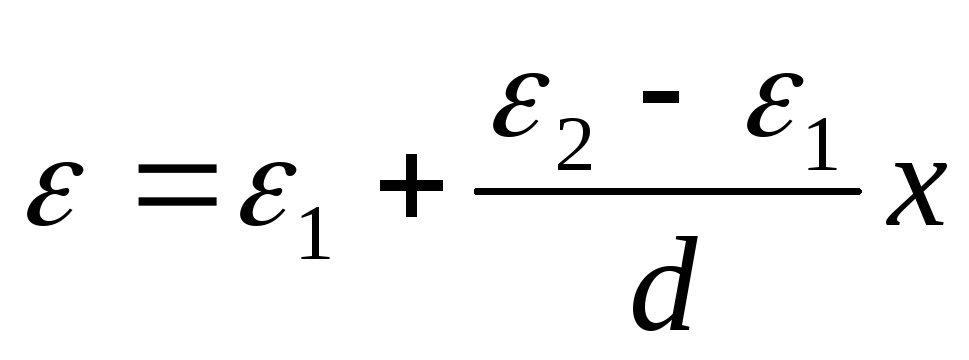 . Etsi levyjen välinen potentiaaliero:
. Etsi levyjen välinen potentiaaliero:
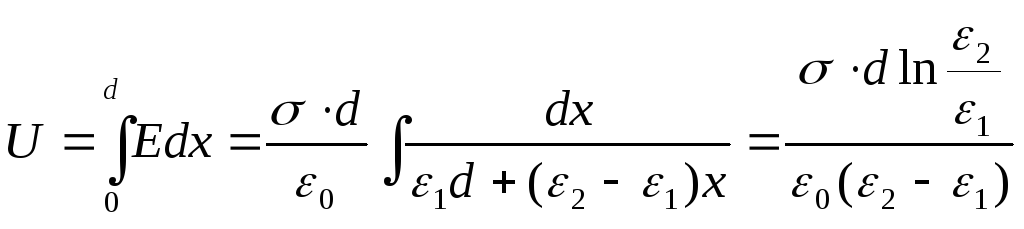
Kondensaattorin kapasitanssi on
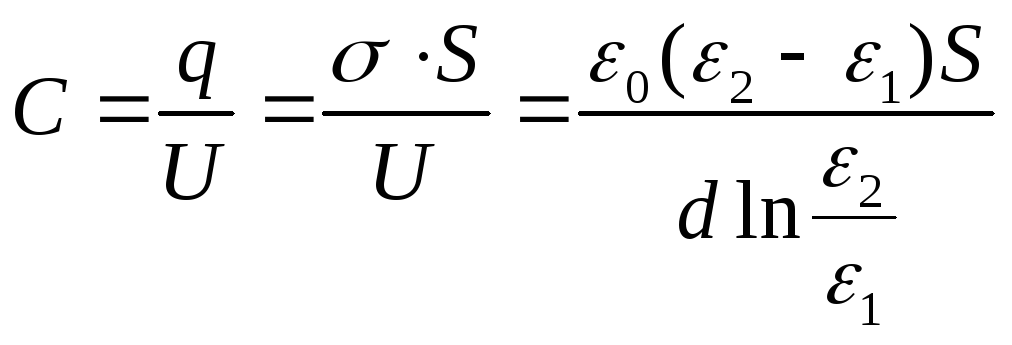
Vastaus:
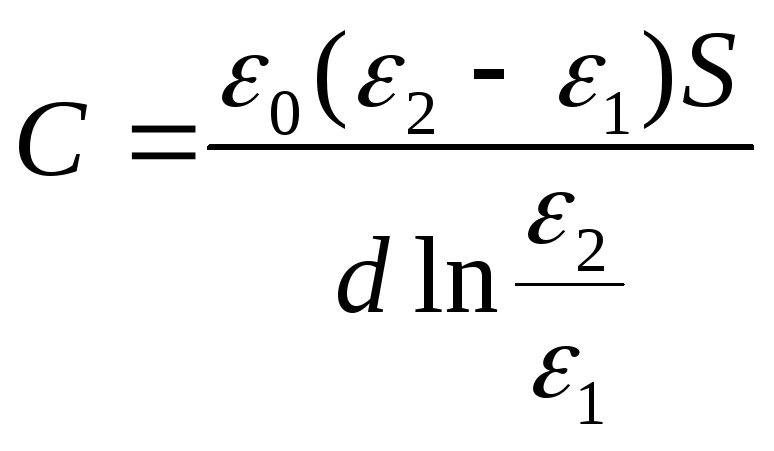
Esimerkki 12.7. Tasaisen kondensaattorin levyjen välissä, joka on ladattu potentiaalieroon U , kaksi eristekerrosta asetetaan yhdensuuntaisesti sen levyjen kanssa. Kerrosten paksuus ja eristeiden permittiivisyys ovat vastaavastid 1 , d 2 , ε 1 , ε 2 . Määritä sähköstaattisten kenttien voimakkuus dielektrisissä kerroksissa.
Annettu: U; d 1 , d 2 , ε 1 , ε 2
Löytö: E 1 , E 2 .
Ratkaisu . Kondensaattorilevyjen yli oleva jännite, kun otetaan huomioon, että kenttä kussakin dielektrisessä kerroksessa on tasainen,
U=E1d1 +E2d2. (1)
Sähköinen siirtymä molemmissa dielektrisissä kerroksissa on sama, joten voimme kirjoittaa
D=D1=D2= ε 0 ε 1 E 1 = ε 0 ε 2 E 2 (2)
Lausekkeista (1) ja (2) löydämme halutun
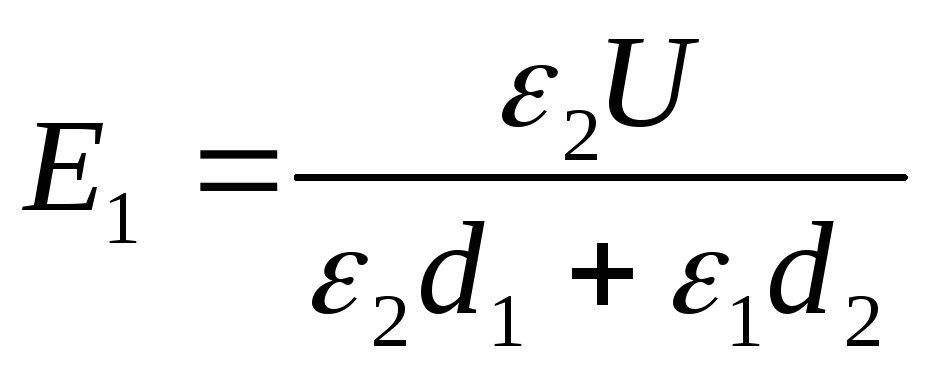 (3)
(3)
Kaavasta (2) seuraa, että
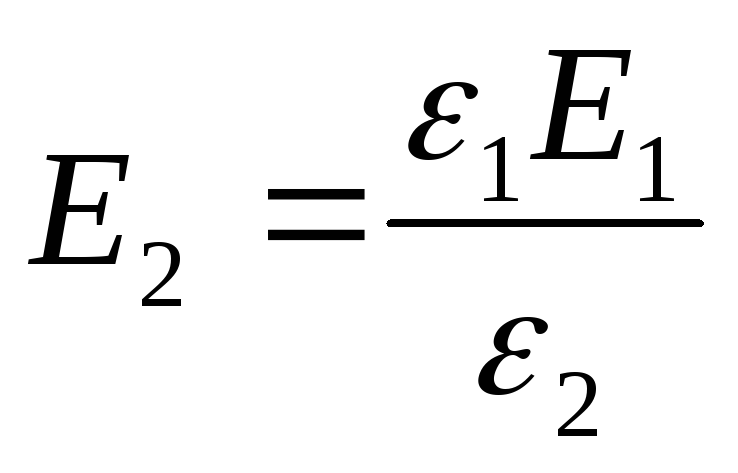
Vastaus:
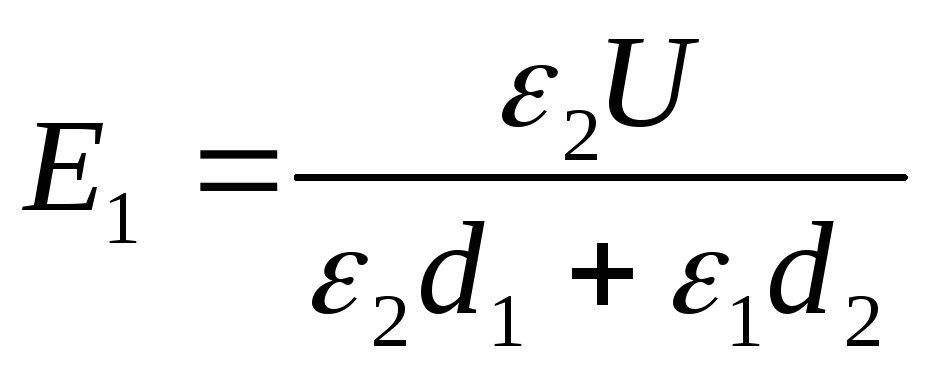 ;
;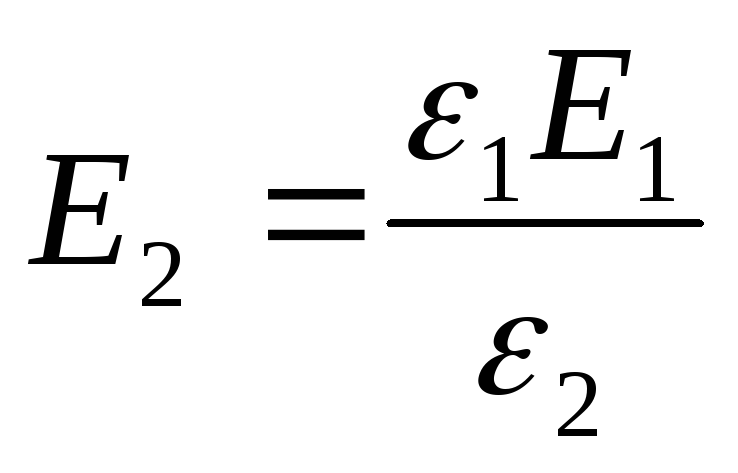
Esimerkki 12.7. Levyn alue S litteä kondensaattori on 100 cm 2 . Levyjen välinen tila täytetään tiiviisti kahdella eristekerroksella - kiillelevyllä (ε 1 =7) paksu d 1 = 3,5 mm ja parafiini (ε 2 =2) paksuus d 2 = 5 mm. Määritä tämän kondensaattorin kapasitanssi.
Annettu: S= 100 cm 2 =10 -2 m 2 ; ε 1 =7; d 1 =3,5mm = 3,5∙10 -3 m;, e 1 =2; d 1 =3,5mm = 5∙10 -3 m;
Löytö: KANSSA.
Ratkaisu . Kondensaattorin kapasiteetti
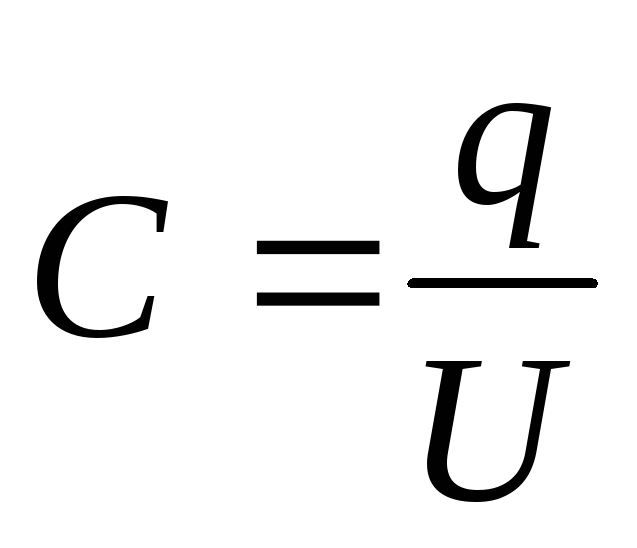
jossa = - varaus kondensaattorilevyillä (- pintavaraustiheys levyillä); \u003d - levyjen potentiaaliero, joka on yhtä suuri kuin dielektristen kerrosten jännitteiden summa: U \u003d U 1 +U 2. Sitten
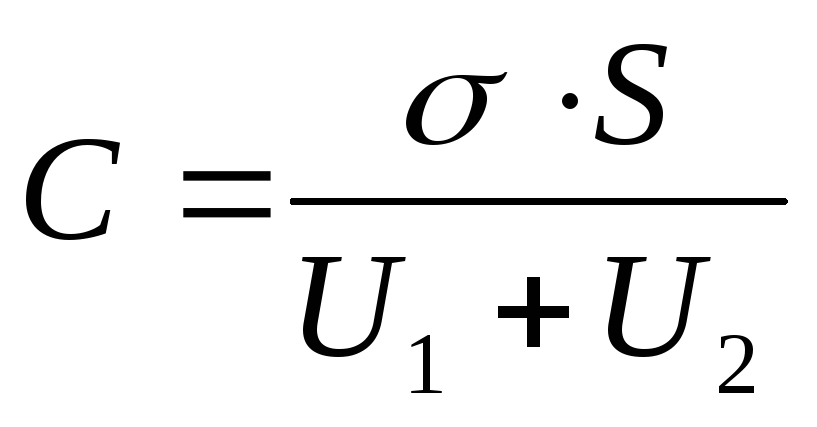 (1)
(1)
Jännitteet U 1 ja U 2 löytyvät kaavoista
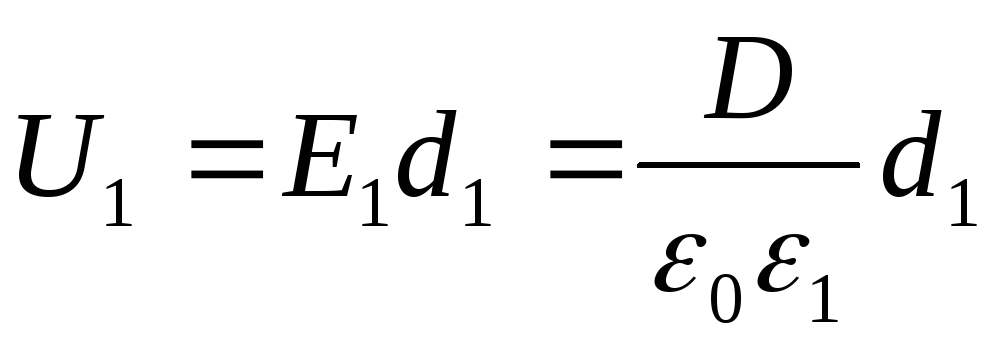 ;
;
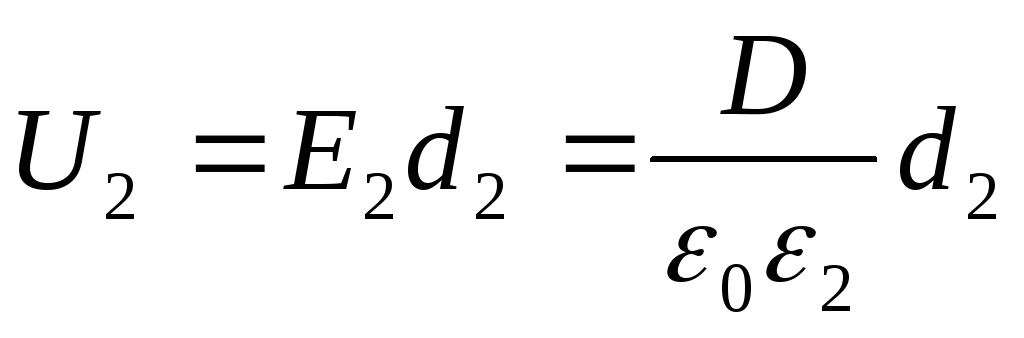 (2)
(2)
jossa E1 ja E2 - sähköstaattisen kentän voimakkuus dielektrisen aineen ensimmäisessä ja toisessa kerroksessa; D on sähköinen siirtymä dielektrissä (sama molemmissa tapauksissa). Ottaen huomioon sen
Ja annettu kaava (2), lausekkeesta (1) löydämme kondensaattorin halutun kapasitanssin
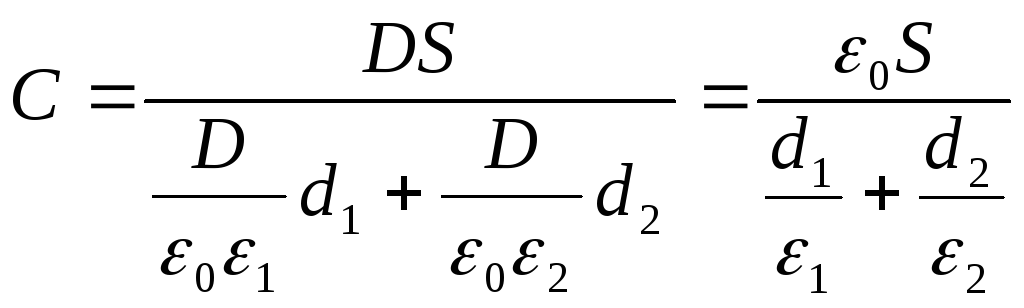
Vastaus: C \u003d 29,5 pF.
Esimerkki 12.7. Kolmen kondensaattorin akku, jotka on kytketty sarjaan C 1 \u003d 1 μF; KANSSA 2 \u003d 2uF ja C 3 \u003d 4 μF on kytketty EMF-lähteeseen. Kondensaattorin akun lataus q \u003d 40 μC. Määritä: 1) jännite U 1 , U 2 Ja U 3 jokaisessa kondensaattorissa; 2) EMF-lähde; 3) kondensaattoripankin kapasiteetti.
Annettu : C 1 \u003d 1 μF = 1 ∙ 10 -6 F; C 2 \u003d 2 μF \u003d 2 ∙ 10 -6 F ja C 3 \u003d 4 μF \u003d 4 ∙ 10 -6 F; q \u003d 40 μC \u003d F 410 -6 .
Etsi: 1) U 1 , U 2 , U 3 ; 2) ξ; 3) C.
Ratkaisu . Kun kondensaattorit kytketään sarjaan, kaikkien levyjen varaukset ovat itseisarvoltaan yhtä suuret
q 1 \u003d q 2 \u003d q 3 \u003d q.
Kondensaattorin jännite
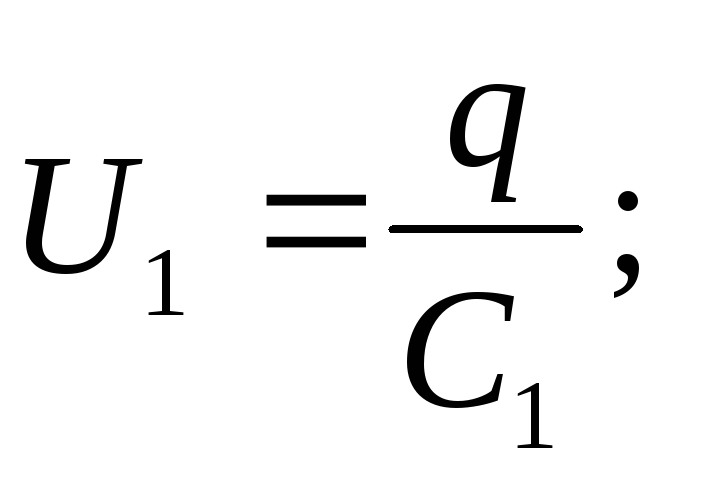
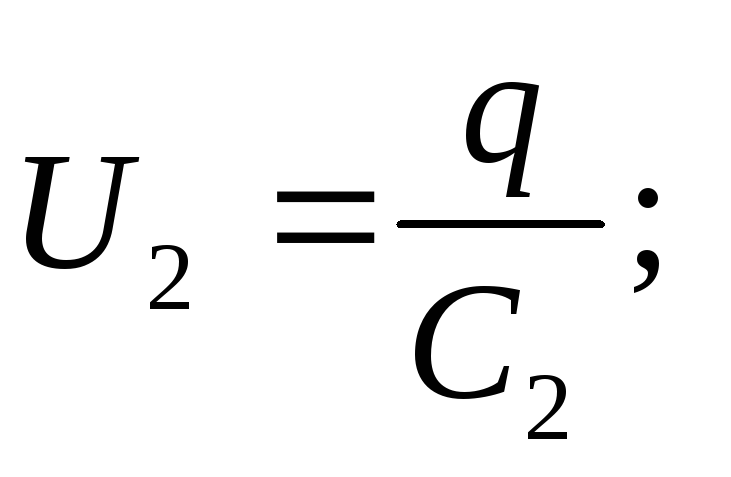
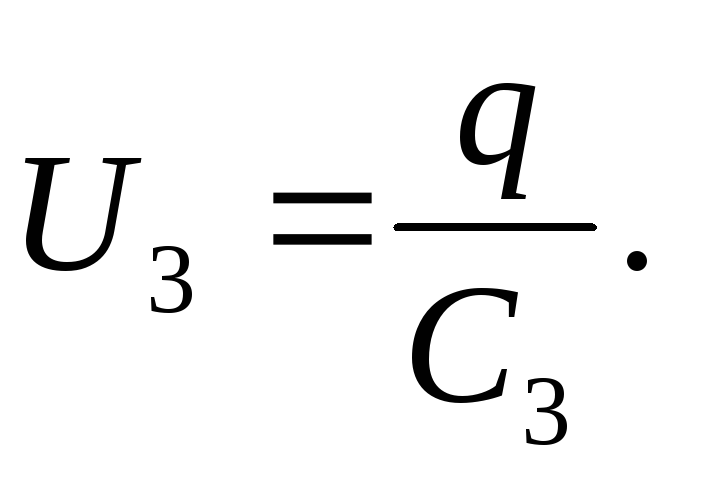
Lähteen EMF on yhtä suuri kuin kunkin sarjaan kytketyn kondensaattorin jännitteiden summa:
ξ \u003d U 1 + U 2 + U 3
Kun se on kytketty sarjaan, kunkin kondensaattorin kapasitanssien käänteisluvut lasketaan yhteen:
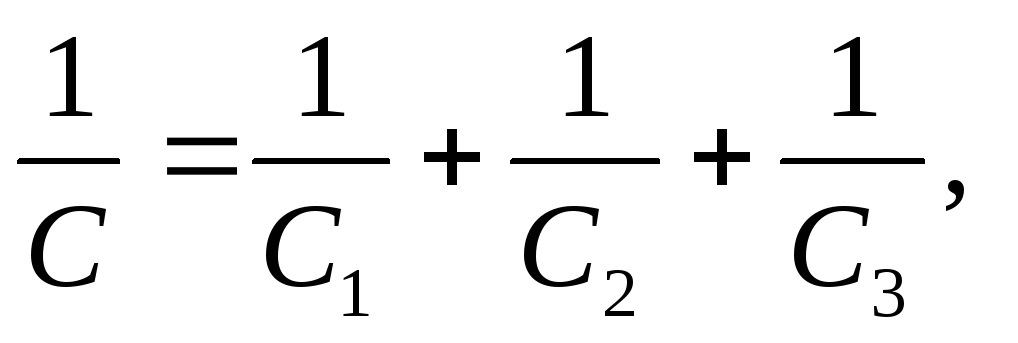
Missä on kondensaattoripankin haluttu kapasiteetti
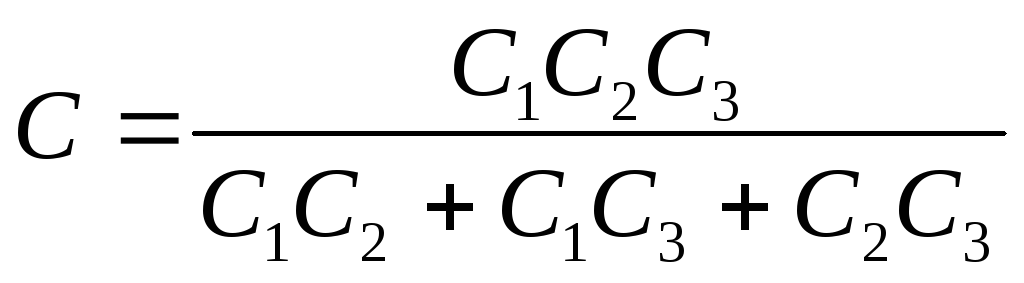
Vastaus: 1) U 1 \u003d 40 V; U 2 \u003d 20 V, U 3 = 10 V; 2) Ɛ= 70V; 3) C \u003d 0,571 µF.
Esimerkki 12.7. Kaksi samankapasiteettista litteää ilmakondensaattoria on kytketty sarjaan ja kytketty EMF-lähteeseen. Kuinka ja kuinka monta kertaa kondensaattorien varaus muuttuu, jos yksi niistä upotetaan öljyyn, jonka dielektrisyysvakio ε=2,2.
Annettu: C 1 \u003d C 2 \u003d C; q \u003d 40 μC \u003d 40 ∙ 10 -6 F ; ε 1 =1; ε 2 =2,2.
Löytö:
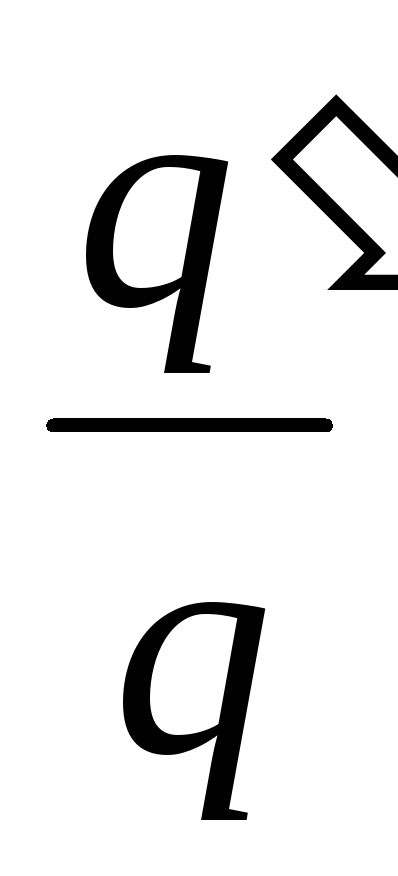 .
.
Ratkaisu . Kun kondensaattorit kytketään sarjaan, molempien kondensaattorien varaukset ovat yhtä suuret. Ennen upottamista dielektriseen (öljyyn) kunkin kondensaattorin varaus
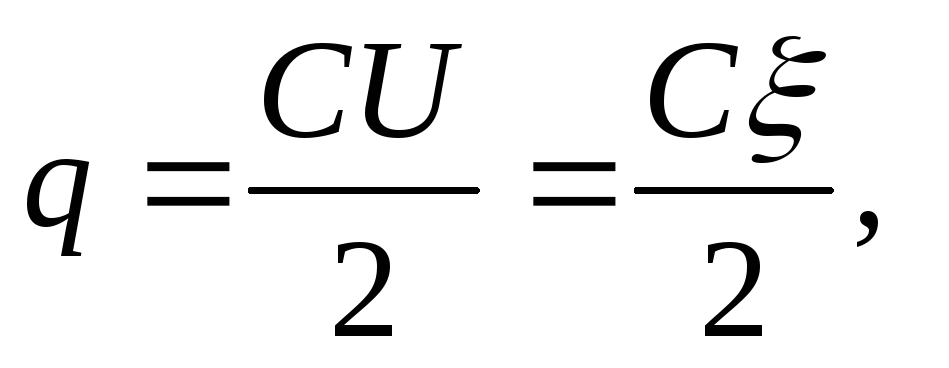
missä ξ \u003d U 1 + U 2 (kun kondensaattorit on kytketty sarjaan, lähteen EMF on yhtä suuri kuin kunkin kondensaattorin jännitteiden summa).
Kun yksi kondensaattoreista on upotettu eristeeseen, kondensaattorien varaukset ovat jälleen samat ja vastaavasti ensimmäisessä ja toisessa kondensaattorissa ovat yhtä suuret.
q = CU 1 = ε 2 CU 2
(ottaen huomioon, että ε 1 =1), josta, jos otamme huomioon, että ξ = U 1 + U 2, saadaan
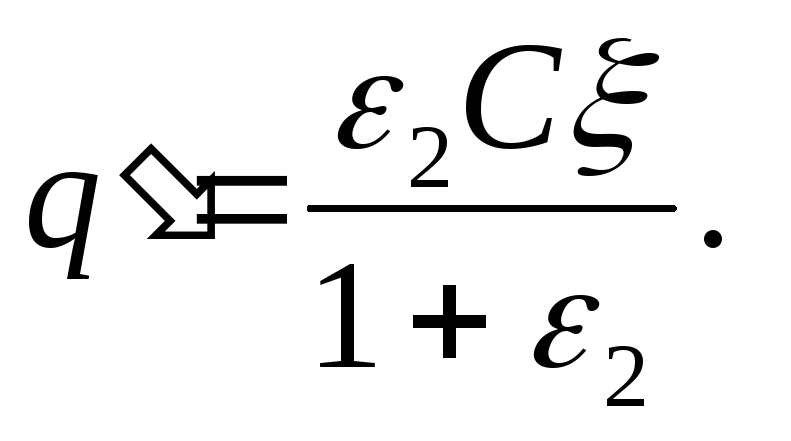 (2)
(2)
Jakamalla (2) (1) saadaan haluttu suhde
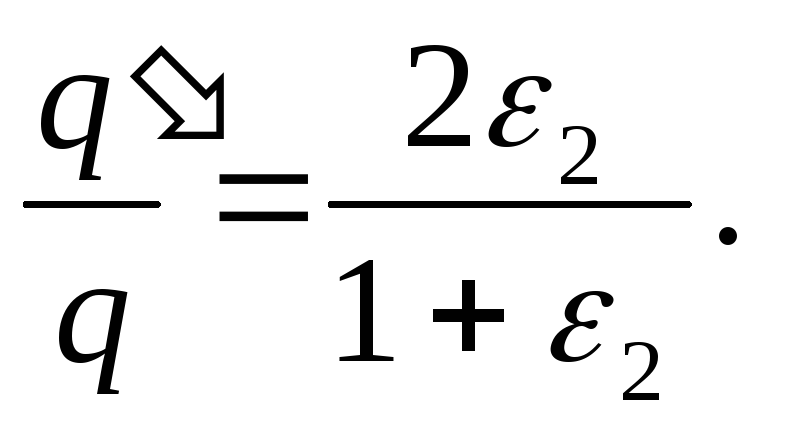
Vastaus:
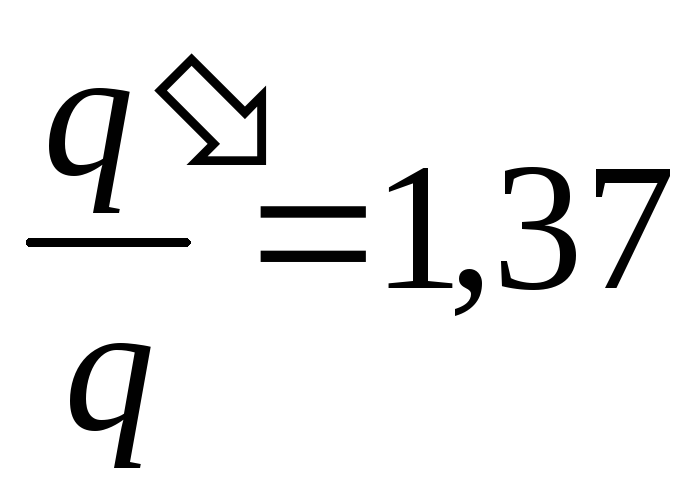 , eli kondensaattorien varaus kasvaa kertoimella 1,37.
, eli kondensaattorien varaus kasvaa kertoimella 1,37.
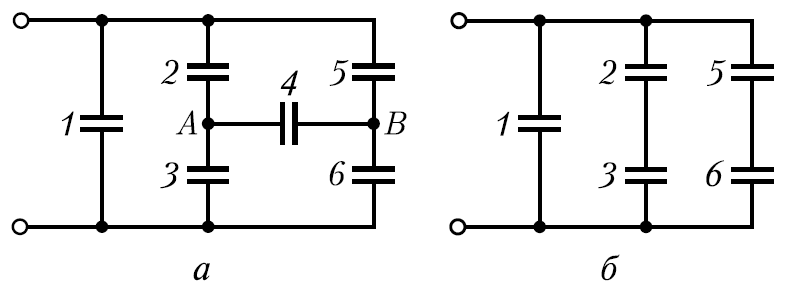
Esimerkki 12.7. Kondensaattorit, joiden kapasitanssi on C, on kytketty kuvan a mukaisesti. määrittää kapasitanssin yleinen tämä kondensaattorien kytkentä. .
 Ratkaisu
.
Jos irrotat kondensaattorin C 4 piiristä, saat kondensaattoreiden kytkennän, joka on helppo laskea. Koska kaikkien kondensaattorien kapasiteetit ovat samat (C 2 \u003d C 3 ja C 5 \u003d C 6), molemmat rinnakkaiset haarat ovat symmetrisiä, joten haaroissa tasaisesti sijaitsevien pisteiden A ja B potentiaalien on oltava samat. Kondensaattori C 4 on siis kytketty pisteisiin, joissa potentiaaliero on nolla. Siksi kondensaattoria C4 ei ole ladattu, ts. se voidaan sulkea pois ja ongelmatilanteessa esitettyä kaaviota voidaan yksinkertaistaa (kuva b).
Ratkaisu
.
Jos irrotat kondensaattorin C 4 piiristä, saat kondensaattoreiden kytkennän, joka on helppo laskea. Koska kaikkien kondensaattorien kapasiteetit ovat samat (C 2 \u003d C 3 ja C 5 \u003d C 6), molemmat rinnakkaiset haarat ovat symmetrisiä, joten haaroissa tasaisesti sijaitsevien pisteiden A ja B potentiaalien on oltava samat. Kondensaattori C 4 on siis kytketty pisteisiin, joissa potentiaaliero on nolla. Siksi kondensaattoria C4 ei ole ladattu, ts. se voidaan sulkea pois ja ongelmatilanteessa esitettyä kaaviota voidaan yksinkertaistaa (kuva b).
Tämä piiri koostuu kolmesta rinnakkaisesta haarasta, joista kahdessa on kaksi kondensaattoria sarjassa.
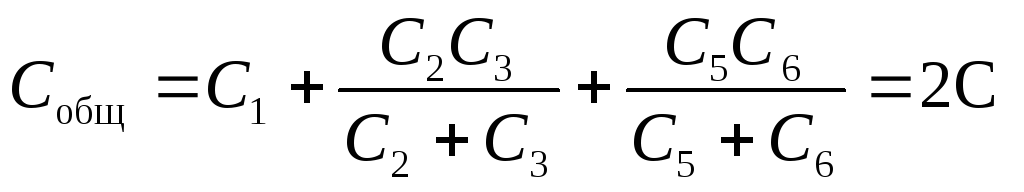
Vastaus: C yhteensä = 2C.
Esimerkki 12.7. Litteä lauhdutin teholla C 1 \u003d 4pF ladattu potentiaalieroonU 1 = 100V. Kun kondensaattori oli irrotettu jännitelähteestä, kondensaattorilevyjen välinen etäisyys kaksinkertaistui. Määritä: 1) potentiaalieroU 2 kondensaattorilevyillä niiden erottamisen jälkeen; 2) ulkoisten voimien työ työntää levyjä erilleen.
Annettu: C 1 \u003d 4pF \u003d 4 ∙ 10 -12 F; U 1 \u003d 100 V; d 2 \u003d 2d 1.
Löytö: 1) U2;2)A.
Ratkaisu . Kondensaattorilevyjen varaus jännitelähteestä irrotuksen jälkeen ei muutu, ts. Q = vakio. Siksi
C 1 U 1 \u003d C 2 U 2, (1)
jossa C 2 ja U 2 ovat vastaavasti kondensaattorilevyjen kapasitanssi ja potentiaaliero sen jälkeen, kun ne on siirretty erilleen.
Ottaen huomioon, että litteän kondensaattorin kapasitanssi 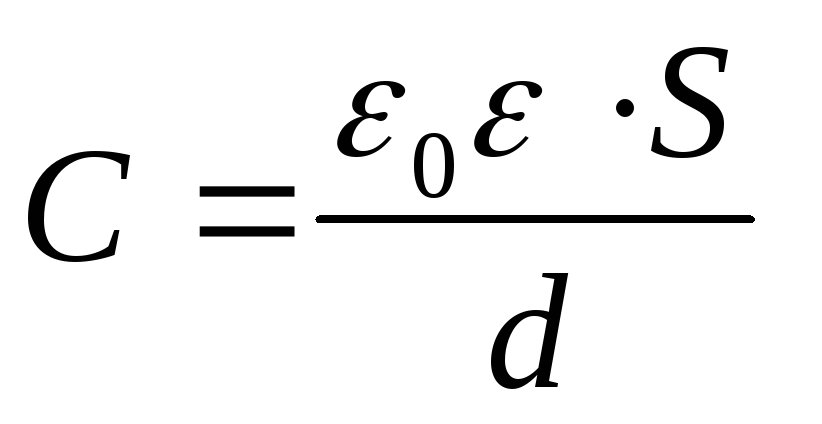 , kaavasta (1) saadaan haluttu potentiaaliero
, kaavasta (1) saadaan haluttu potentiaaliero
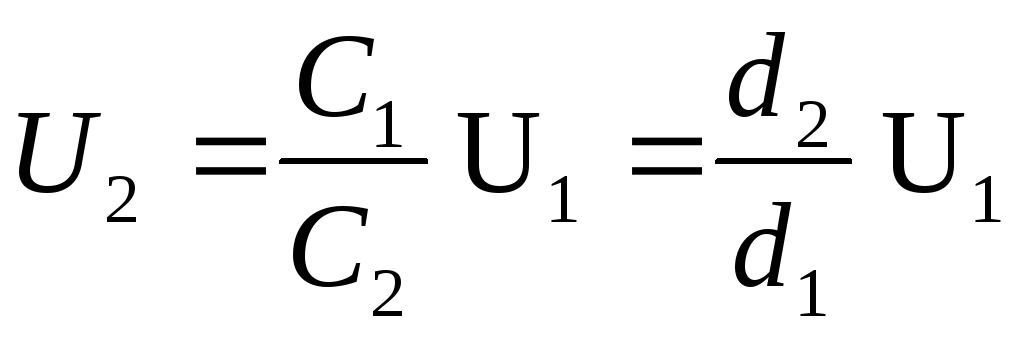 (2)
(2)
Kun kondensaattori on irrotettu jännitelähteestä, kahden varautuneen levyn järjestelmää voidaan pitää suljettuna, jolle energian säilymisen laki täyttyy: ulkoisten voimien työ A on yhtä suuri kuin järjestelmän energian muutos.
A \u003d L 2 - L 1 (3)
missä W 1 ja W 2 ovat kondensaattorikentän energia alku- ja lopputilassa, vastaavasti.
Olettaen että 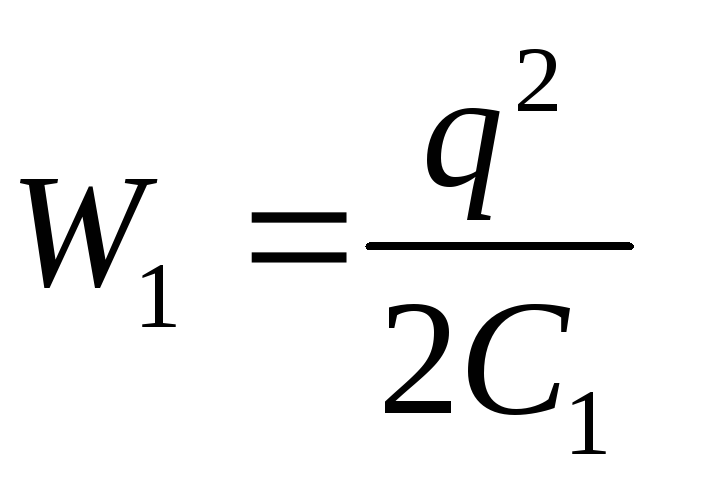 Ja
Ja 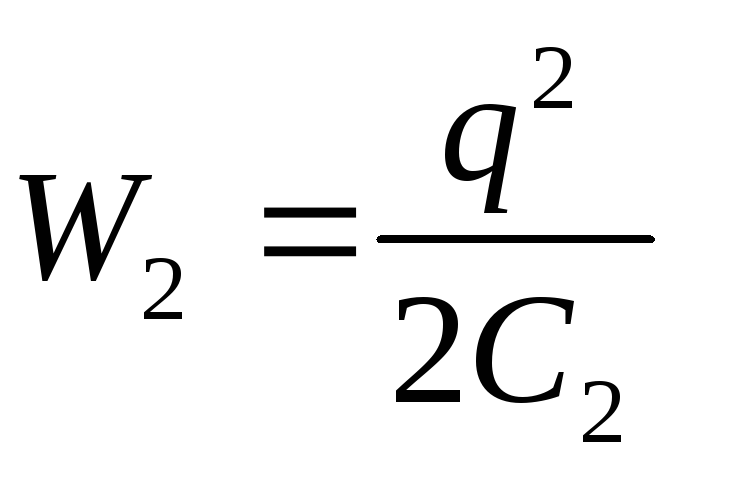 (q – const), kaavasta (3) saadaan haluttu ulkoisten voimien työ
(q – const), kaavasta (3) saadaan haluttu ulkoisten voimien työ
[ottaen huomioon, että q=C 1 U 1 ja kaava (2)].
Vastaus : 1) U 2 \u003d 200 V; 2) A \u003d 40nJ.
Esimerkki 12.7. Kiinteä dielektrinen pallo, jonka sädeR=5cm ladattu tasaisesti irtotiheydellä ρ=5nC/m 3 . Määritä palloa ympäröivän tilan sähköstaattisen kentän energia.
Annettu: R = 5 cm = 5-10 -2 m; ρ = 5nC/m 3 = 5∙10 -9 C / m 3.
Löytö: W.
Ratkaisu . Varautuneen pallon kenttä on pallosymmetrinen, joten tilavuusvaraustiheys on sama kaikissa pisteissä, jotka sijaitsevat yhtä etäisyydellä pallon keskustasta.
E 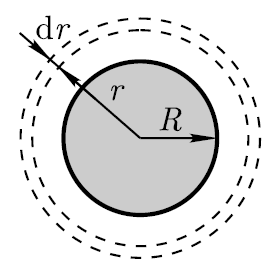 energia elementaarisessa pallomaisessa kerroksessa (se valitaan eristeen ulkopuolelta, jossa energia tulisi määrittää) tilavuudella dV (katso kuva)
energia elementaarisessa pallomaisessa kerroksessa (se valitaan eristeen ulkopuolelta, jossa energia tulisi määrittää) tilavuudella dV (katso kuva)
missä dV = 4πr 2 dr (r on elementaarisen pallomaisen kerroksen säde; dr on sen paksuus); 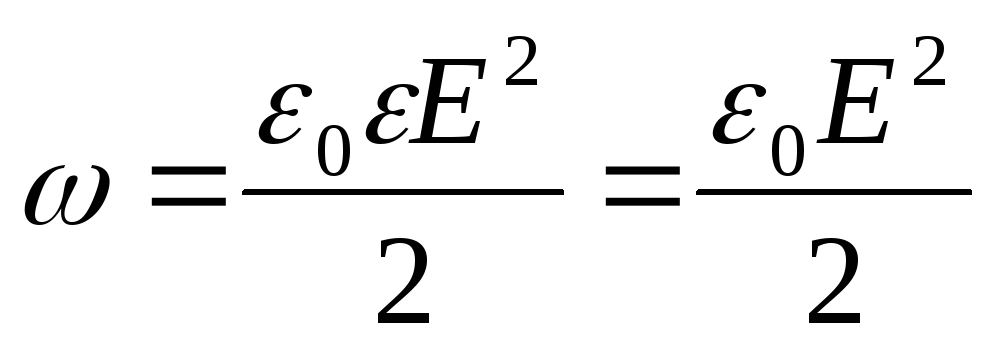 (ε=1 – kenttä tyhjiössä; E – sähköstaattinen kentän voimakkuus).
(ε=1 – kenttä tyhjiössä; E – sähköstaattinen kentän voimakkuus).
Löydämme Gaussin lauseen avulla intensiteetin E kentällä tyhjiössä ja valitsemme mentaalisesti pallon, jonka säde on r suljetuksi pinnaksi (katso kuva). Tällöin koko pallon panos, joka muodostaa tarkasteltavan kentän, pääsee pinnan sisään ja Gaussin lauseen mukaan
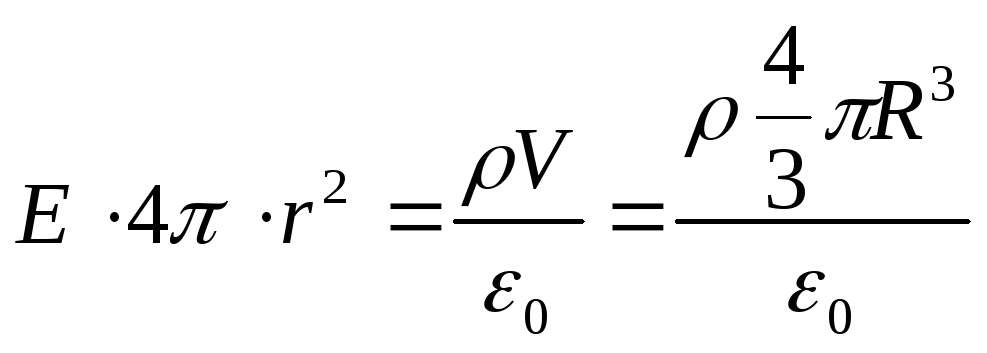
Missä 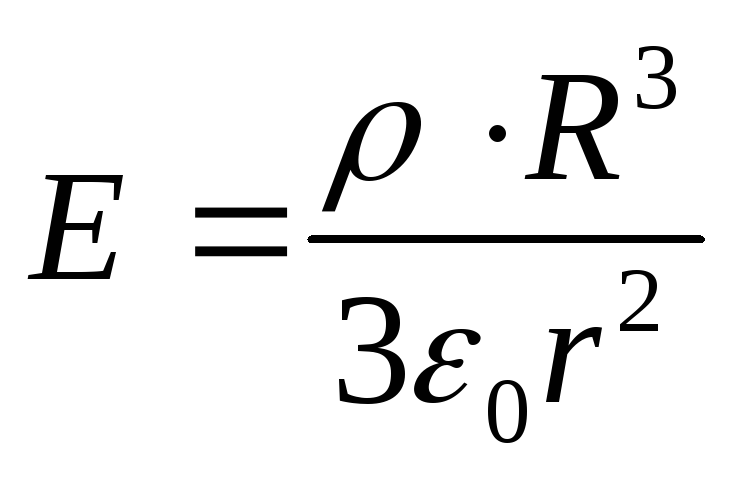
Korvaamalla löydetyt lausekkeet kaavaan (1) saadaan
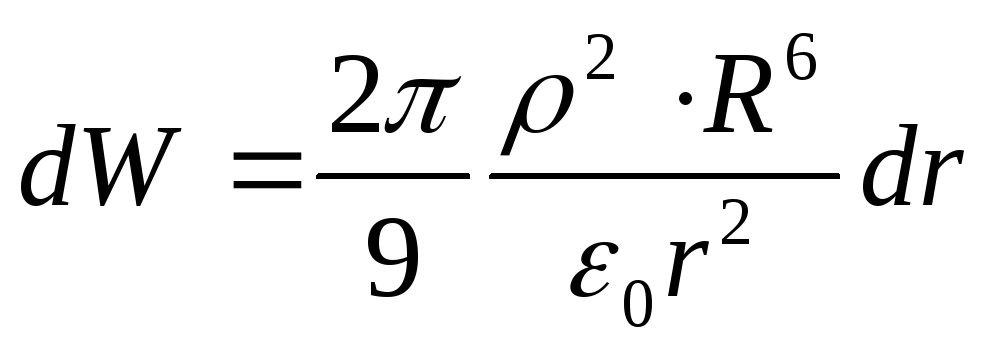
Palloa ympäröivän tilan sisältämä energia,
Vastaus: L = 6,16∙10 -13 J.
Esimerkki 12.7. Tasokondensaattori levyjen pinta-alallaSja niiden välinen etäisyys ℓ varaus ilmoitetaanq, jonka jälkeen kondensaattori irrotetaan jännitelähteestä. Määritä vetovoimaFkondensaattorilevyjen väliin, jos levyjen välisen väliaineen dielektrisyysvakio on yhtä suuri kuin ε.
Annettu : S; ℓ; q; ε .
Löytö: F.
Ratkaisu . Kondensaattorilevyjen varaus jännitelähteestä irrotuksen jälkeen ei muutu, ts. q=vakio. Oletetaan, että vetovoiman F vaikutuksesta kondensaattorilevyjen välinen etäisyys on muuttunut d:llä ℓ . Silloin voima F toimii
Energian säilymislain mukaan tämä työ on yhtä suuri kuin kondensaattorin energiahäviö, ts.
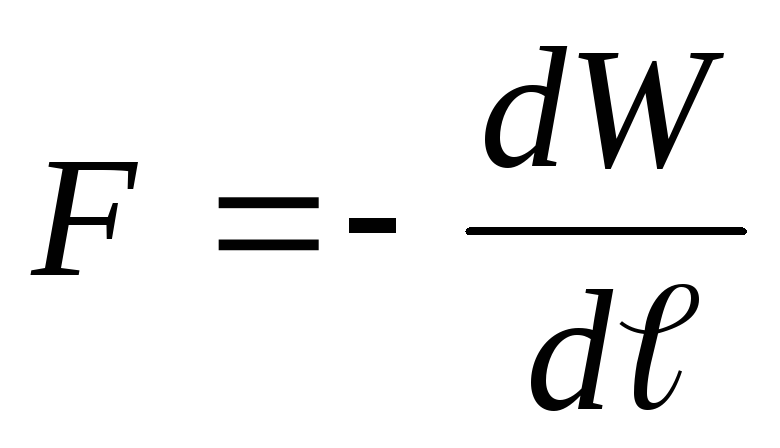 .
(3)
.
(3)
Korvaaminen varautuneen kondensaattorin energian kaavaan 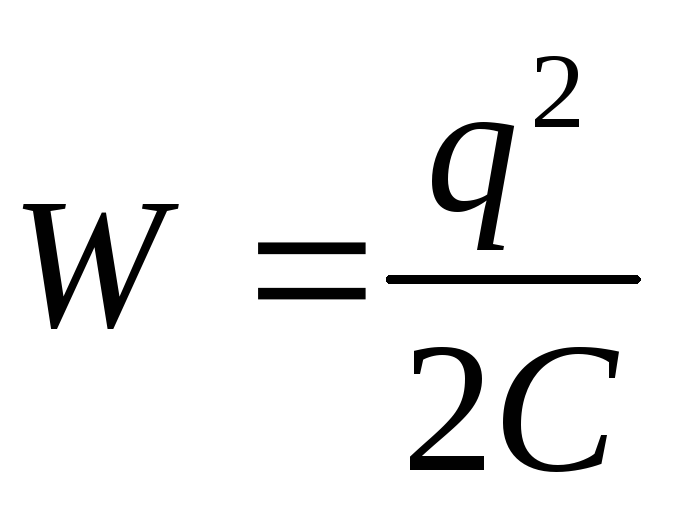 tasaisen kondensaattorin kapasitanssin lauseke
tasaisen kondensaattorin kapasitanssin lauseke 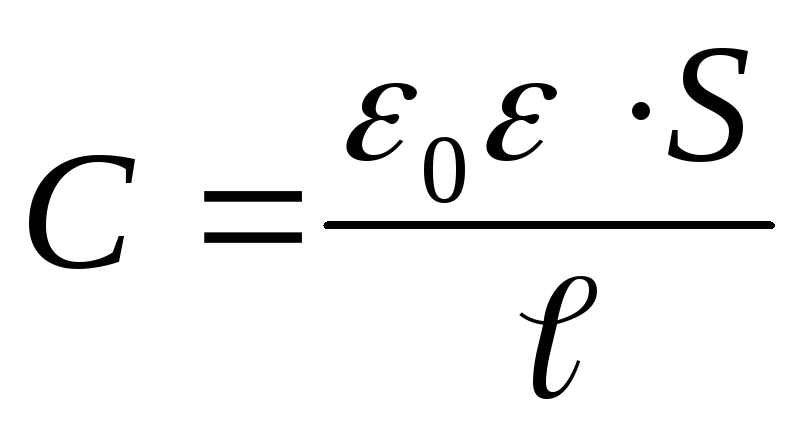 , saamme
, saamme
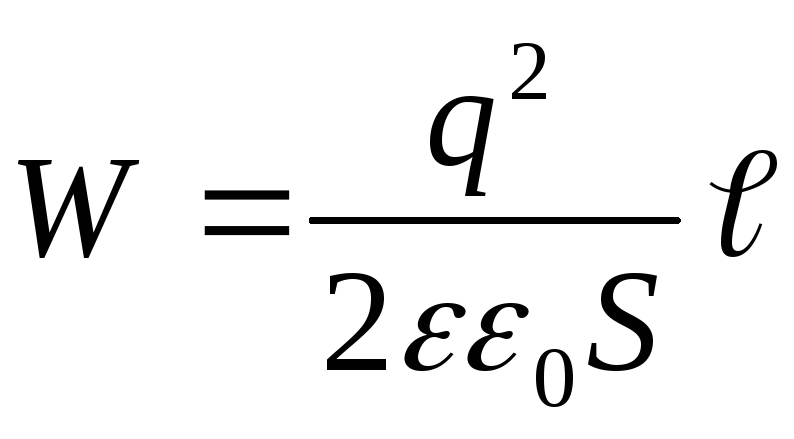 (4)
(4)
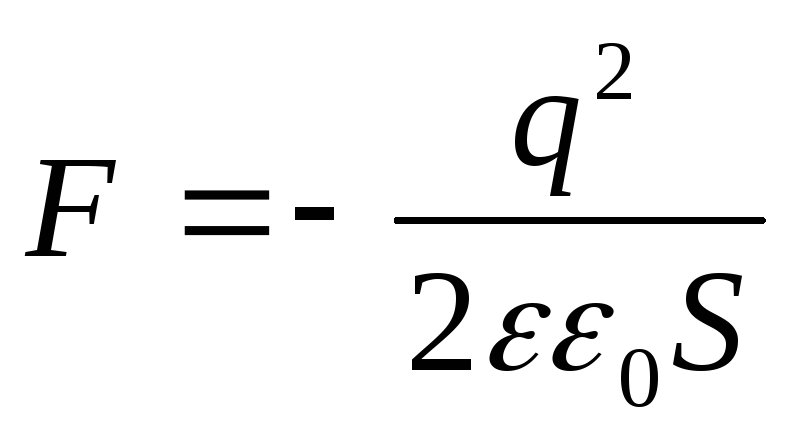
Vastaus:
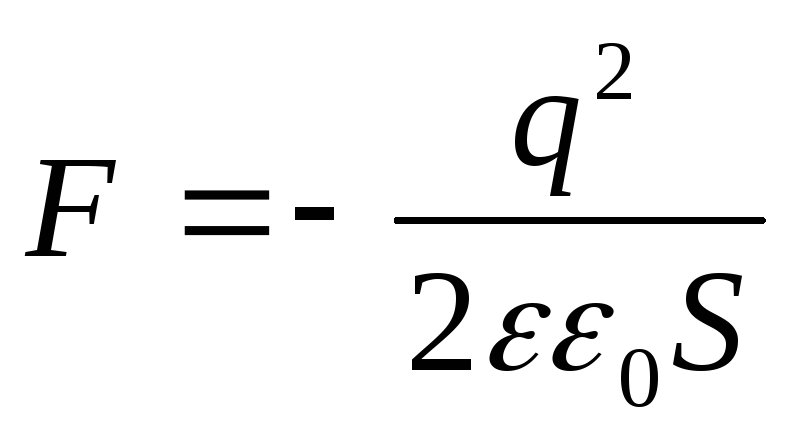
Esimerkki 12.7. TasolevykondensaattoriSja niiden välinen etäisyys ℓ kytketty vakiojännitelähteeseenU. Määritä vetovoimaFkondensaattorilevyjen väliin, jos levyjen välisen väliaineen dielektrisyysvakio on yhtä suuri kuin ε.
Annettu : S; ℓ; U; ε .
Löytö: F.
Ratkaisu . Kondensaattorilevyillä ylläpidetään ongelman tilanteen mukaan vakiojännite, ts. U = vakio Oletetaan, että vetovoiman F vaikutuksesta kondensaattorilevyjen välinen etäisyys on muuttunut dℓ. Silloin voima F toimii
Energian säilymislain mukaan tämä työ menee tässä tapauksessa kondensaattorin energian lisäämiseen (vertaa edelliseen tehtävään), ts.
josta saamme lausekkeiden (1) ja (2) perusteella
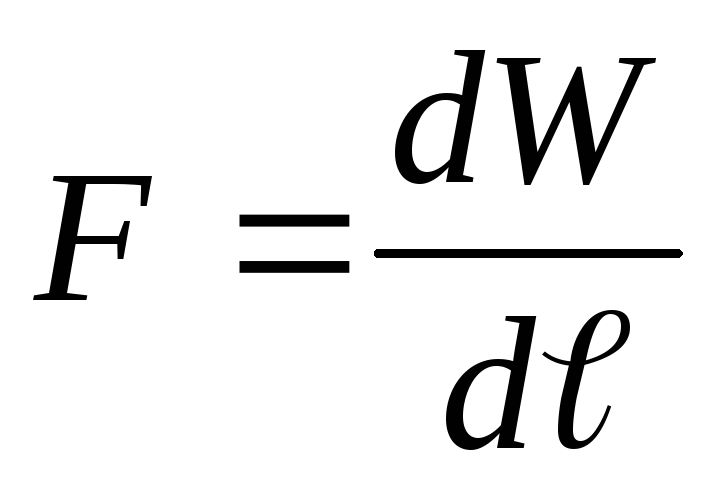 (3)
(3)
Korvaaminen kondensaattorin energian kaavaan 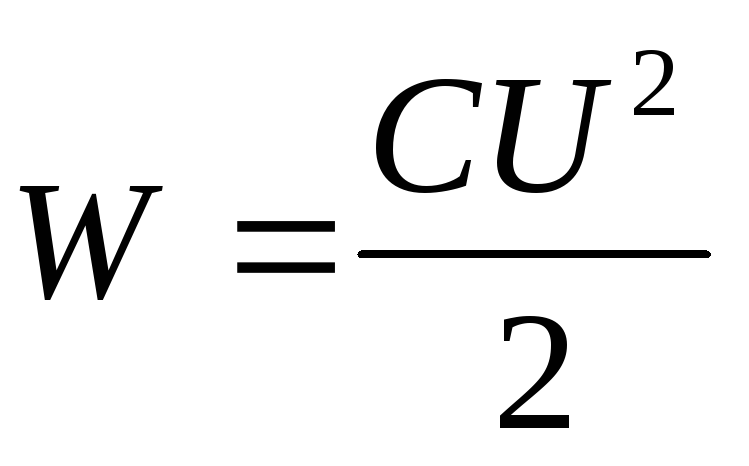 tasaisen kondensaattorin kapasitanssin lauseke
tasaisen kondensaattorin kapasitanssin lauseke  , saamme
, saamme
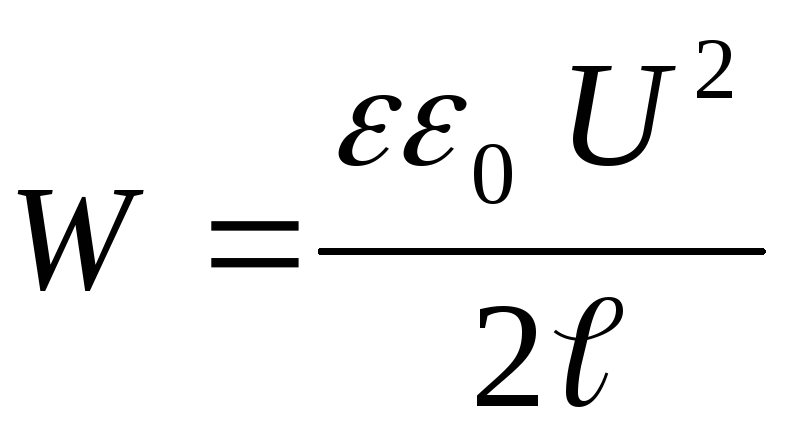 (4)
(4)
Korvaamalla energia-arvon (4) kaavaan (3) ja suorittamalla differentioinnin, löydämme halutun vetovoiman kondensaattorilevyjen välillä
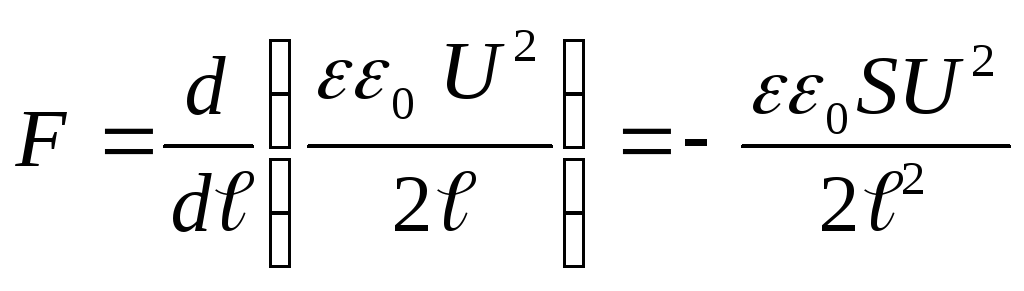 .
.
jossa "-"-merkki osoittaa, että voima F on vetovoima.
Vastaus
: